决策树的优势就在于数据形式非常容易理解,而kNN的最大缺点就是无法给出数据的内在含义。
1:简单概念描述
决策树的类型有很多,有CART、ID3和C4.5等,其中CART是基于基尼不纯度(Gini)的,这里不做详解,而ID3和C4.5都是基于信息熵的,它们两个得到的结果都是一样的,本次定义主要针对ID3算法。下面我们介绍信息熵的定义。
事件ai发生的概率用p(ai)来表示,而-log2(p(ai))表示为事件ai的不确定程度,称为ai的自信息量,sum(p(ai)*I(ai))称为信源S的平均信息量—信息熵。
ID3的原理是基于信息熵增益达到最大,设原始问题的标签有正例和负例,p和n表示其相应的个数。则原始问题的信息熵为
其中N为该特征所取值的个数,比如{rain,sunny},则N即为2
Gain = BaseEntropy – newEntropy
ID3的原理即使Gain达到最大值。信息增益即为熵的减少或者是数据无序度的减少。
ID3易出现的问题:如果是取值更多的属性,更容易使得数据更“纯”(尤其是连续型数值),其信息增益更大,决策树会首先挑选这个属性作为树的顶点。结果训练出来的形状是一棵庞大且深度很浅的树,这样的划分是极为不合理的。 此时可以采用C4.5来解决
C4.5的思想是最大化Gain除以下面这个公式即得到信息增益率:
其中底为2
2:Python代码的实现
from math import log import operator import book.three.myplot as mplt #计算信息熵 def calcShannonEnt(dataSet): numEntries=len(dataSet) #计算数据集中实例的总数 labelCounts={} for featVec in dataSet: currentLabel=featVec[-1] if currentLabel not in labelCounts.keys(): labelCounts[currentLabel]=0 labelCounts[currentLabel]+=1 #创建一个字典,它的键值是最后一列的数值,每个键值都记录了当前类别出现的次数 shannonEnt=0.0 for key in labelCounts: prob=float(labelCounts[key])/numEntries shannonEnt-=prob*log(prob,2) return shannonEnt #生成数据 def createDataSet(): dataSet=[[1,1,'yes'], [1,1,'yes'], [1,0,'no'], [0,1,'no'], [0,1,'no']] labels=['no surfacing','flippers'] return dataSet,labels #划分数据集 def splitDataSet(dataSet,axis,value): #3个参数分别是,待划分的数据集,划分数据集的特征,特征的返回值 retDataSet=[] for featVec in dataSet: if featVec[axis]==value: reducedFeatVec=featVec[:axis] #从索引位置0开始到索引位置axis结束 reducedFeatVec.extend(featVec[axis+1:]) #从索引位置axis+1开始到最终位置结束 retDataSet.append(reducedFeatVec) return retDataSet #选择最好的特征划分 def chooseBestFeatureToSplit(dataSet): numFeatures=len(dataSet[0])-1 baseEntropy=calcShannonEnt(dataSet) #计算整个数据集的原始香农熵,保存最初的无须度量值 bestInfoGain=0.0 bestFeature=-1 for i in range(numFeatures): #遍历数据集中的所有特征,创建唯一的分类标签列表 featList=[example[i] for example in dataSet] uniqueVals=set(featList) newEntropy=0.0 for value in uniqueVals: subDataSet=splitDataSet(dataSet,i,value) #遍历当前特征中的所有唯一属性值,对每个特征划分一次数据集,计算每种划分的信息熵,并对所有唯一特征值得到的熵求和 prob=len(subDataSet)/float(len(dataSet)) newEntropy+=prob*calcShannonEnt(subDataSet) infoGain=baseEntropy-newEntropy if(infoGain>bestInfoGain): #计算最好的信息增益的值 bestInfoGain=infoGain bestFeature=i return bestFeature """ 注意:这里数据集需要满足以下两个办法: <1>所有的列元素都必须具有相同的数据长度 <2>数据的最后一列或者每个实例的最后一个元素是当前实例的类别标签。 """ #如果一个中间节点中数据没有其他特征了,只有一个类别标签,但是类别便签也表示的不是同一个类,则这个时候需要选择最大的那个 def majorityCnt(classList): classCount={} for vote in classList: if vote not in classCount.keys:classCount[vote]=0 classCount[vote]+=1 sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True) return sortedClassCount[0][0] #用递归的方法生成决策树 Python用字典类型来存储树的结构 返回的结果是myTree-字典 def createTree(dataSet,labels): classList=[example[-1] for example in dataSet] if classList.count(classList[0])==len(classList): #类别完全相同则停止继续划分 return classList[0] if len(dataSet[0])==1: #遍历完所有特征时(此时dataSet只有一个类标签)返回出现次数最多的 return majorityCnt(classList) bestFeat=chooseBestFeatureToSplit(dataSet) bestFeatLabel=labels[bestFeat] myTree={bestFeatLabel:{}} #myTree存储了树的所以信息 del(labels[bestFeat]) #当前数据集选取的最好的特征存储在变量bestFeat中,得到列表包含的所有属性值 featValues=[example[bestFeat] for example in dataSet] #选择最优特征的那一列的所有的值 uniqueVals=set(featValues) for value in uniqueVals: subLabels=labels[:] myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLabels) return myTree #使用本例中的数据集 dataSet,labels=createDataSet() print(dataSet)dataSet[0][-1]='maybe' #二维数组,中的第一行的最后一个元素myTree=createTree(dataSet,labels)print(myTree)
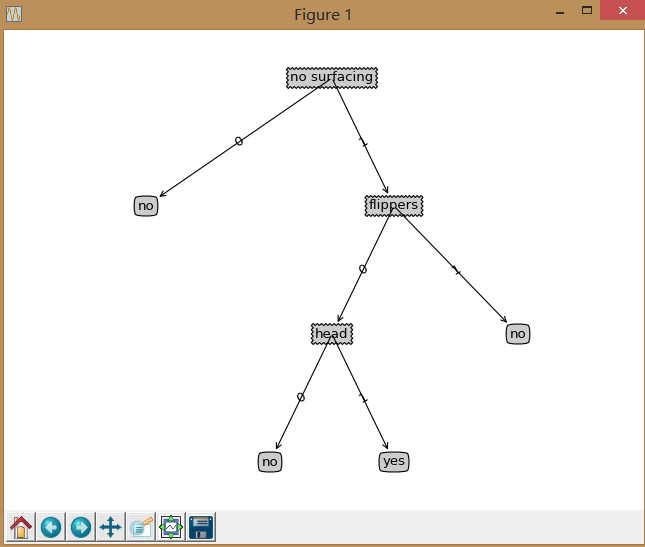
3:在python中使用Matplotlib注解绘制树形图
Matplotlib提供了一个注解工具annotations,非常有用,它可以在数据图形上添加文本注释。注解通常用于解释数据的内容。
这段代码我也没看懂,所以只给出书上代码
#使用决策树执行分类 def classify(inputTree, featLabels, testVec): firstStr = inputTree.keys()[0] secondDict = inputTree[firstStr] featIndex = featLabels.index(firstStr) #index方法查找当前列表中第一个匹配firstStr变量的元素的索引 for key in secondDict.keys(): if testVec[featIndex] == key: if type(secondDict[key]).__name__ == 'dict': classLabel = classify(secondDict[key], featLabels, testVec) else: classLabel = secondDict[key] return classLabel
决策树的存储
构造决策树是一个很耗时的任务。为了节省计算时间,最好能够在每次执行分类时调用已经构造好的决策树。为了解决这个问题,需要使用python模块pickle序列化对象,序列化对象可以在磁盘上保存对象,并在需要的时候读取出来。
#决策树的存储 def storeTree(inputTree, filename): #pickle序列化对象,可以在磁盘上保存对象 import pickle fw = open(filename, 'w') pickle.dump(inputTree, fw) fw.close() def grabTree(filename): #并在需要的时候将其读取出来 import pickle fr = open(filename) return pickle.load(fr)
4:使用决策树预测隐形眼镜类型
#从文件中读取数据集,先转化为,模型中需要的数据集的形式 fr=open('lenses.txt') lenses=[inst.strip().split(' ') for inst in fr.readlines()] lensesLabels=['age','prescript','astigmatic','tesrRate'] lensesTree=createTree(lenses,lensesLabels) mplt.createPlot(lensesTree) #print(lensesTree) #print(lenses) #print(lensesLabels)
注明:本笔记来源于书籍<机器学习实战>