一、独立性检验
根据频数信息判断两类因子彼此相关或相互独立的假设检验。
p-value
p-value就是Probability的值,它是一个通过计算得到的概率值,也就是在原假设为真时, 得到最大的或者超出所得到的检验统计量值的概率。
一般将p值定位到0.05,当 p < 0.05 拒绝原假设,p > 0.05,接受原假设。
1.卡方检验 chisq.test()
假设检验(Hypothesis Testing)是数理统计学中根据一定假设条件由样本推断总体的一种方法。
原假设————没有发生;
备择假设————发生了;
具体作法:
根据问题的需要对所研究的总体作某种假设,记作H0 ;选取合适的统计量,这个统计量的选取要使得在假设H0成立时,其分布为已知;由实测的样本,计算出统计量的值,并根据预先给定的显著性水平进行检验,作出拒绝或接受假设H0的判断。

2.Fisher检验 fisher.test()
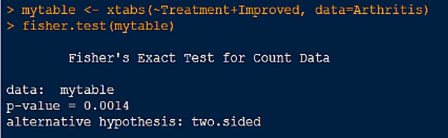
3.Cochran-Mantel-Haenszel检验
三变量之间的显著关系


二、相关性分析函数
相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。简单来说就是变量之间是否有关系。
1.相关性衡量指标
Pearson相关系数、Spearman相关 系数、Kendall相关系数、偏相关系数、多分格( polychoric )相关系数和多系列( polyserial )相关系数
数据:
美国各个州的人口,文盲率,预期寿命、犯罪率等指标

2.cor() 函数,相关性分析
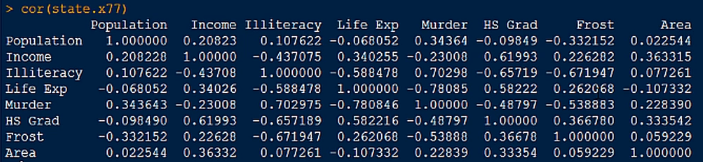
3.cov() 函数,协方差。计算偏相关系数时要使用到协方差的结果

计算一组变量与另一组变量的关系

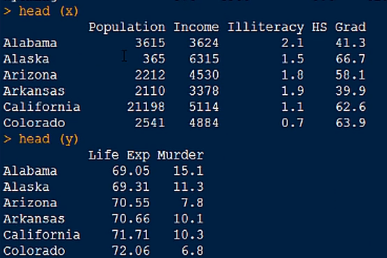



三、相关性检验函数
置信区间 confidence interval
指由样本统计量所构成的总体参数的估计区间。在统计学中,一个概率样本的置信区间是对这个样本的某个总体函数的区间估计。置信区间展现的是这个参数的真实值有一定概率落在测量结果周围的程度。置信区间给出的是被测量参数的测量值的可信程度。
非参数检验 Nonparametric tests
在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。由于非参数检验的方法在推断过程中不涉及有关总体分布的函数,因而得名为“非参数”检验。
参数检验 Parametric tests
是在总体分布形式已知的情况下,对总体分布的参数如均值、方差等进行推断的方法。也就是数据分布已知,比如满足正态分布。
1.cor.test() 函数,检测两个变量之间的置信区间和相关性系数
检测文盲率与谋杀率的关系

2.corr.test() 函数,检测两个变量之间的置信区间和相关性系数
3.ggm包下的 pcor.test() 函数

