直接插入排序

【基本思想】

　　把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。 

 

【算法复杂度】

时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
O(n^2)	O(n^2)	O(n)	O(1)	稳定

时间复杂度>>>

　　如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需（n-1）次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1）次。平均来说插入排序算法的时间复杂度为O(n^2）。因而，插入排序不适合对于数据量比较大的排序应用，但是，如果需要排序的数据量很小，例如，量级小于千，那么插入排序还是一个不错的选择。 

算法稳定性>>>

        插入排序是在一个已经有序的小序列的基础上，一次插入一个元素。当然，刚开始这个有序的小序列只有1个元素，就是第一个元素。比较是从有序序列的末尾开始，也就是想要插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

 

【动图演示】

 

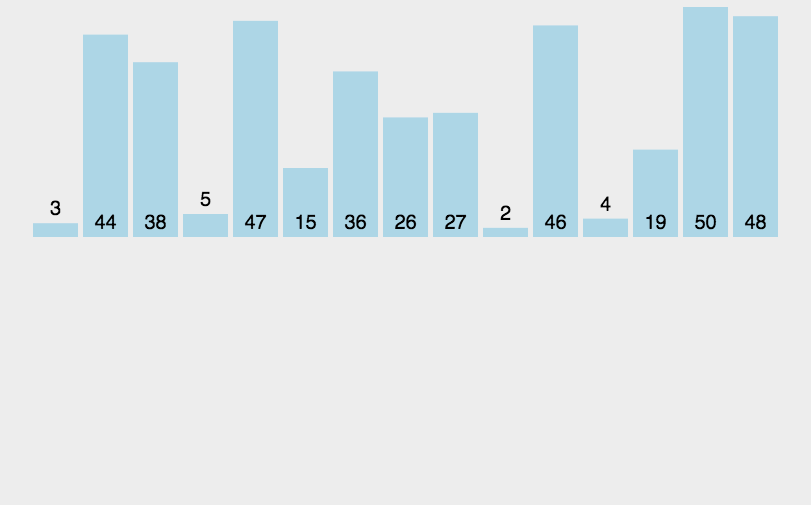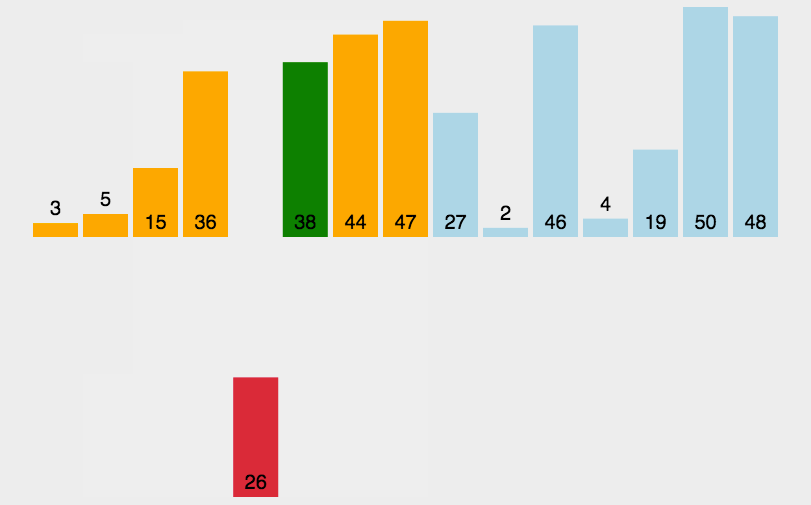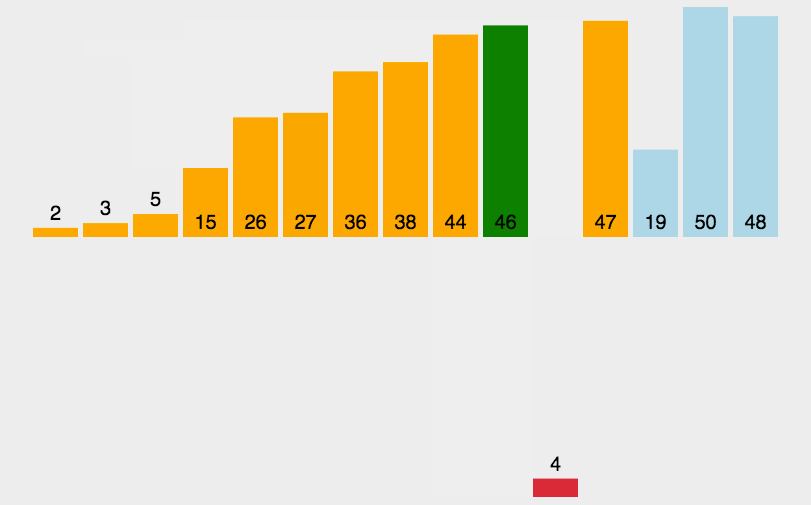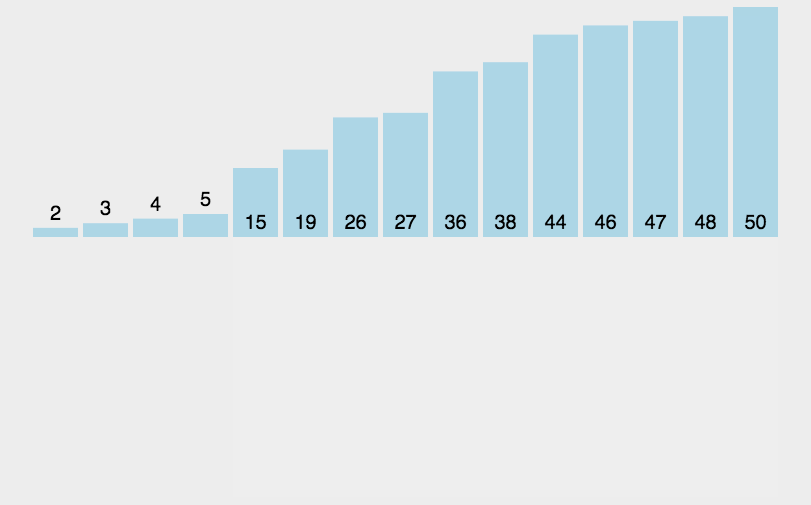
【算法实现】

/*
** 直接插入排序的C++实现
** 1.设置监视哨r[0]，将待插入记录的值赋值给r[0]；
** 2.设置开始查找的位置j；
** 3.在数组中进行搜索，搜索中将第j个记录后移，直至r[0].key≥r[j].key为止；
** 4.将r[0]插入r[j+1]的位置上。
*/

void insertSort(vector<int>& seq) {
    seq.insert(seq.begin(), 0);
    int length = seq.size(); // 待排序序列的长度
    for (int i = 2; i < length; i++) {
        if (seq[i] < seq[i - 1]) { // 当待插入元素小于前一个元素时
            seq[0] = seq[i];  // 将待插入的元素移动到首位
            int j = i - 1;
            while (seq[0] < seq[j]) { // 依次将已排好序的元素与待插入元素比较
                seq[j + 1] = seq[j];  // 如果待排序元素小于当前元素，当前元素后移一位
                j--;
            }
            seq[j + 1] = seq[0];  // 将待排序元素插入到正确的位置
        }
    }
    seq.erase(seq.begin());
}

【算法优化】

　　将直接插入排序中寻找seq[i]的插入位置的方法改为采用折半比较，即可得到折半插入排序算法。在处理seq[i]时，seq[0]……seq[i-1]已经按值排好序。所谓折半比较，就是在插入seq[i]时，取seq[i-1/2]的值与seq[i]的值进行比较，如果seq[i]的值小于seq[i-1/2]的值，则说明seq[i]只能插入seq[0]到seq[i-1/2]之间，故可以在seq[0]到seq[i-1/2-1]之间继续使用折半比较；否则只能插入seq[i-1/2]到seq[i-1]之间，故可以在seq[i-1/2+1]到seq[i-1]之间继续使用折半比较，如此反复，直到最后能够确定插入的位置为止。

/*
** 二分插入排序的C++实现
** 假设:对N个类型为int的整数值进行排序
** 每次采用折半查找的方式从已排好序的序列中定位插入位置
** 当high小于low时，查找结束，在high之后插入待排序的元素
*/

void insertSort2(vector<int>& seq) {
    int wait = seq[0];
    int length = seq.size(); // 待排序序列的长度
    for (int i = 1; i < length; i++) {
        if (seq[i] < seq[i - 1]) { // 当待插入元素小于前一个元素时
            wait = seq[i];  // 保存待插入的元素值到wait
            int low = 0, high = i - 1, mid = (high + low) / 2;
            /* 折半查找要插入的位置 */
            while (high >= low) {  // high小于low时终止查找
                if (wait < seq[mid])
                    high = mid - 1;
                else
                    low = mid + 1;
                mid = (high + low) / 2;
            }
            for (int j = i - 1; j > high; j--)
                seq[j + 1] = seq[j];  // 向后移动元素
            seq[high + 1] = wait; // 将待排序元素插入到正确的位置
        }
    }
}

下面是直接插入排序与二分插入排序的比较，

作者在 Intel i7四核处理器，Linux x86_64位机上测试了10组大小为1000的整数数组的排序，整数的范围在0~100000之间

/*
** 直接插入排序与二分插入排序的比较
** 数字的规模：10组大小为1000的数组
** 数字的范围：0～100000之间，随机生成
*/

#include<time.h>
#include<vector>
#include<stdlib.h>
#include<iostream>
using namespace std;

void insertSort(vector<int>& seq) {
    int wait = seq[0] , j = 0;
    int length = seq.size(); // 待排序序列的长度
    for (int i = 1; i < length; i++) {
        if (seq[i] < seq[i - 1]) { // 当待插入元素小于前一个元素时
            wait = seq[i];  // 保存待插入的元素值到wait
            j = i - 1;
            while (wait < seq[j]) { // 依次将已排好序的元素与待插入元素比较
                seq[j + 1] = seq[j];  // 如果待排序元素小于当前元素，当前元素后移一位
                j--;
            }
            seq[j + 1] = wait;  // 将待排序元素插入到正确的位置
        }
    }
}

void insertSort2(vector<int>& seq) {
    int wait = seq[0];
    int length = seq.size(); // 待排序序列的长度
    for (int i = 1; i < length; i++) {
        if (seq[i] < seq[i - 1]) { // 当待插入元素小于前一个元素时
            wait = seq[i];  // 保存待插入的元素值到wait
            int low = 0, high = i - 1, mid = (high + low) / 2;
            /* 折半查找要插入的位置 */
            while (high >= low) {  // high小于low时终止比较
                if (wait < seq[mid])
                    high = mid - 1;
                else
                    low = mid + 1;
                mid = (high + low) / 2;
            }
            for (int j = i - 1; j > high; j--)
                seq[j + 1] = seq[j];  // 向后移动元素
            seq[high + 1] = wait; // 将待排序元素插入到正确的位置
        }
    }
}

int main()
{
    vector<int> seq[10];
    vector<int> seq_[10];
    for (int i = 0; i < 10; i++) {
        for (int j = 0; j < 1000; j++)
            seq[i].push_back(rand() % 100000);
    }
    for (int i = 0; i < 10; i++) {
        seq_[i] = seq[i];
    }

    srand((unsigned)time(NULL));

    clock_t start1 = clock();
    for (int i = 0; i < 10; i++) {
        insertSort(seq[i]);
    }
    clock_t ends1 = clock();
    cout << "the algorithm 1 running time : " << (double)(ends1 - start1)/10 / CLOCKS_PER_SEC << endl;

    clock_t start2 = clock();
    for (int i = 0; i < 10; i++) {
        insertSort2(seq_[i]);
    }
    clock_t ends2 = clock();
    cout << "the algorithm 2 running time : " << (double)(ends2 - start2)/10 / CLOCKS_PER_SEC << endl;

    cout << "time 1 / time 2 = " << ((double)(ends1 - start1)/10 / (double)(ends2 - start2)/10)*100 << endl;
    for (int i = 0; i < 10; i++) {
        for (int j = 0; j < seq[i].size(); j++) {
            if (seq_[i][j] - seq[i][j] != 0) {
                cout << "sorted error!";
                break;
            }
        }
    }
    return 0;
}

 实验截图：

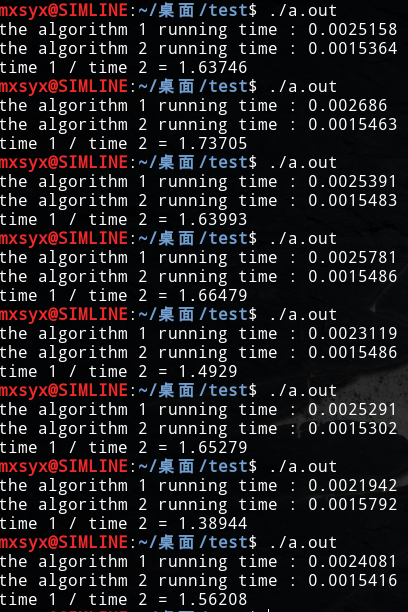
可以看到，二分插入排序比直接插入排序的速度快1.5倍左右，当然受到各方面因素的影响，实验结果未必准确，但采用折半的方式的确节省了不少时间。