邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图:一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n×n的方阵,定义为:
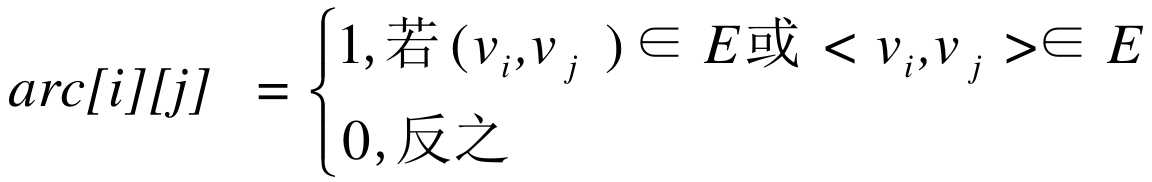
无向图的邻接矩阵:

1.我们要判定任意两顶点是否有边无边就非常容易了。
2.我们要知道某个顶点的度,其实就是这个顶点v i 在邻接矩阵中第i行(或第i列)的元素之和。比如顶点v 1 的度就是1+0+1+0=2
3.求顶点v i 的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点。
有向图的邻接矩阵:

有向图讲究入度与出度,顶点v 1 的入度为1,正好是第v 1 列各数之和。顶点v 1 的出度为2,即第v 1 行的各数之和。
与无向图同样的办法,判断顶点v i 到v j 是否存在弧,只需要查找矩阵中arc[i][j]是否为1即可。要求v i 的所有邻接点就是将矩阵第i行元素扫描一遍,查找arc[i][j]为1的顶点。
带权图的邻接矩阵:
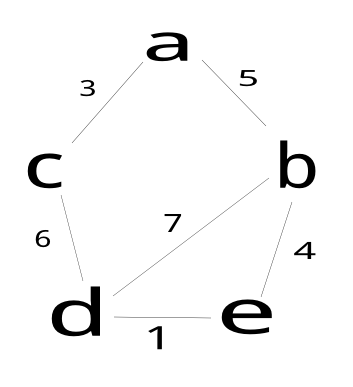
将上图转换成一个邻接矩阵

/* * 带权无向图的邻接矩阵 */ #define MAXVEX 100 #define INFINITY 65535 typedef char vtype; // 结点类型 typedef int etype; // 边权类型 typedef struct{ vtype vexs[MAXVEX]; // 顶点表 etype arc[MAXVEX][MAXVEX]; // 邻接矩阵,可看作边表 int vertexes, edges; // 图中当前的顶点数和边数 } Graph; void createGraph(Graph *graph){ int i, j, k, w; printf("输入结点数和边数: "); scanf("%d%d", &graph->vertexes, &graph->edges); /* 读入顶点信息,建立顶点表 */ printf("输入结点信息: "); for (i = 0; i < graph->vertexes; i++) scanf(&graph->vexs[i]); /* 邻接矩阵初始化 */ for (i = 0; i < graph->vertexes; i++) for (j = 0; j <graph->vertexes; j++) graph->arc[i][j] = INFINITY; /* 读入edges条边,建立邻接矩阵 */ printf("输入边(vi,vj)上的下标i,下标j和权w: "); for (k = 0; k < graph->edges; k++){ scanf("%d%d%d", &i, &j, &w); graph->arc[i][j] = w; graph->arc[j][i] = w; // 因为是无向图,矩阵对称 } }
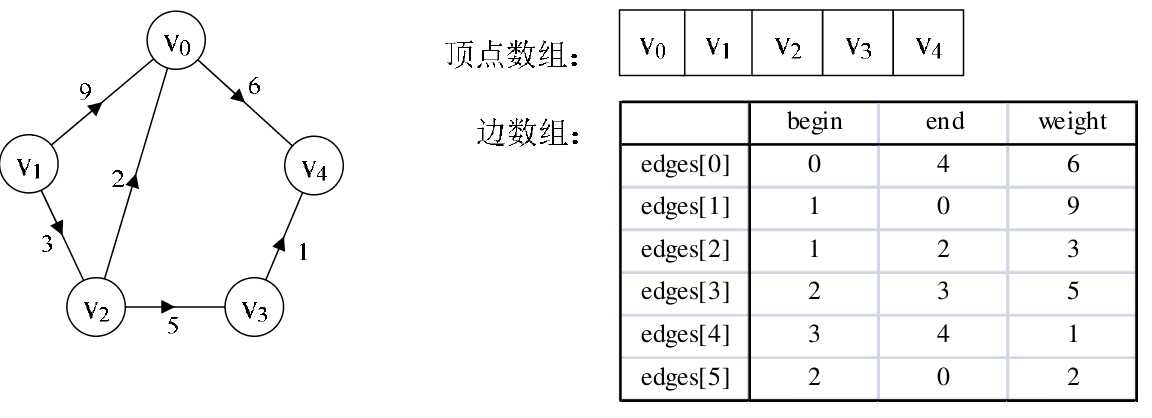
边集数组
边集数组由两个一维数组构成;一个是存储顶点的信息,另一个是存储边的信息;这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成。显然边集数组关注的是边的集合,在边集数组中要查找一个顶点的度需要扫描整个边数组,效率并不高,因此它更适合对边依次进行处理的操作,而不适合对顶点相关的操作。
邻接表
- 图中顶点用一个一维数组存储,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
- 图中每个顶点v i 的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点v i 的边表,有向图则称为顶点v i 作为弧尾的出边表。
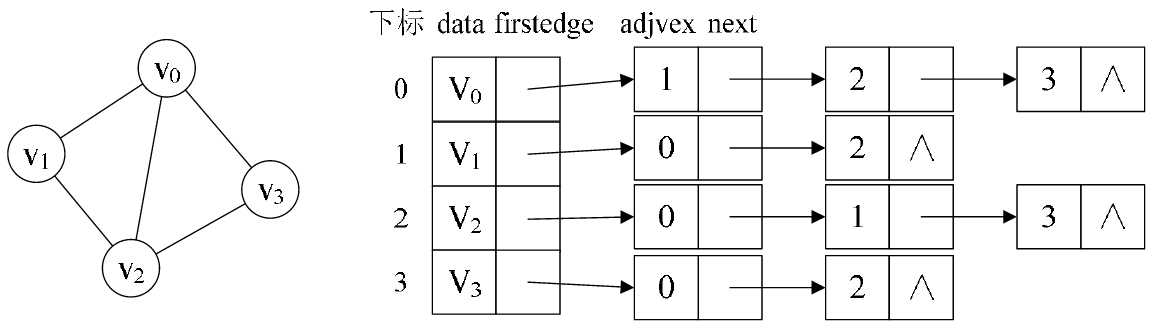
1. 从图中我们知道,顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。
2. 边表结点由adjvex和next两个域组成,adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。
3. 这样的结构,对于我们要获得图的相关信息也是很方便的。比如我们要想知道某个顶点的度,就去查找这个顶点的边表中结点的个数。若要判断顶点Vi 到Vj 是否存在边,只需要测试顶点Vi 的边表中adjvex是否存在结点Vj 的下标j就行了,若求顶点的所有邻接点,其实就是对此顶点的边表进行遍历,得到的adjvex域对应的顶点就是邻接点。
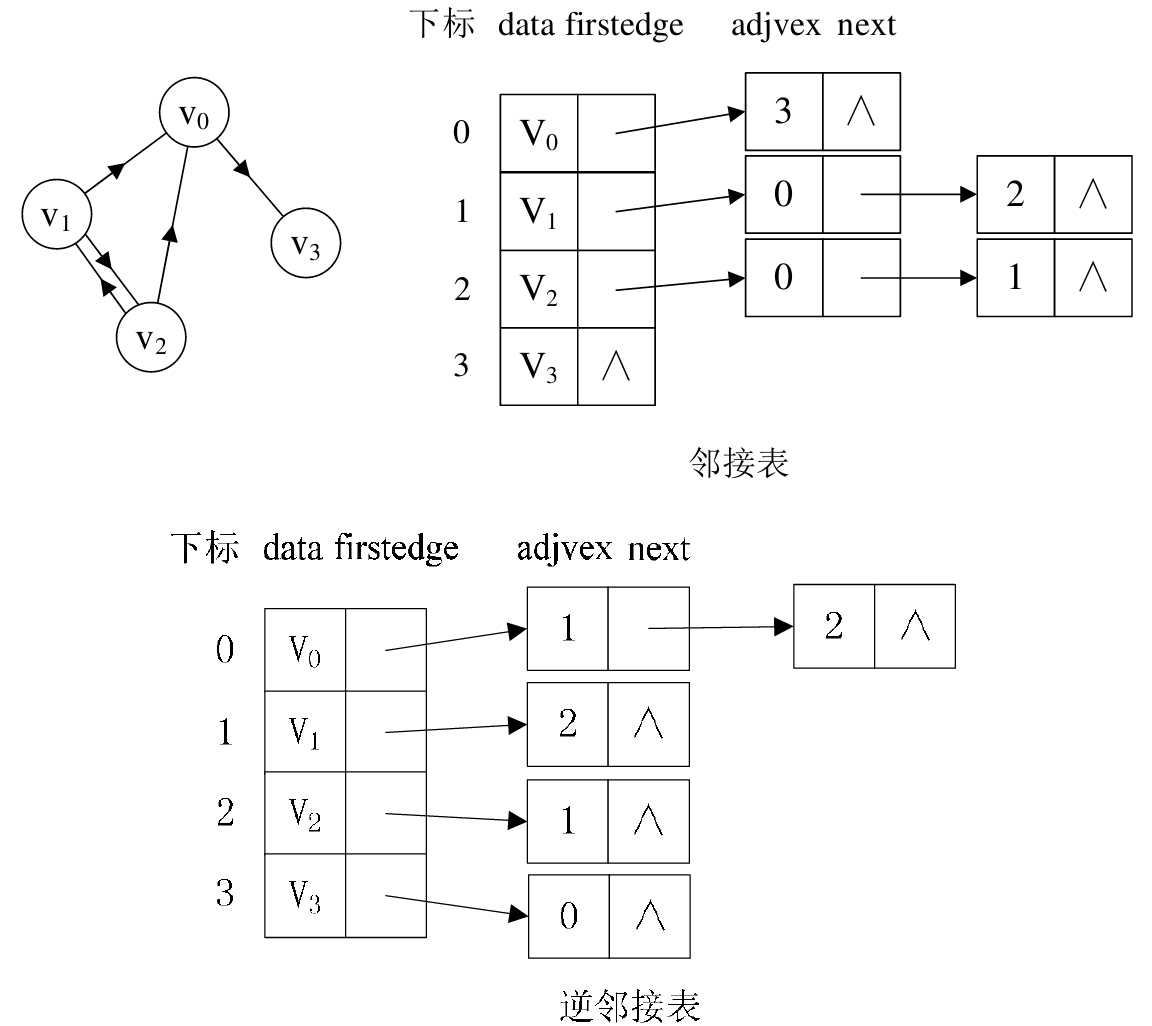
若是有向图,邻接表结构是类似的,但要注意的是有向图由于有方向,我们是以顶点为弧尾来存储边表的,这样很容易就可以得到每个顶点的出度。但也有时为了便于确定顶点的入度或以顶点为弧头的弧,我们可以建立一个有向图的逆邻接表,即对每个顶点Vi 都建立一个链接为 Vi 为弧头的表。
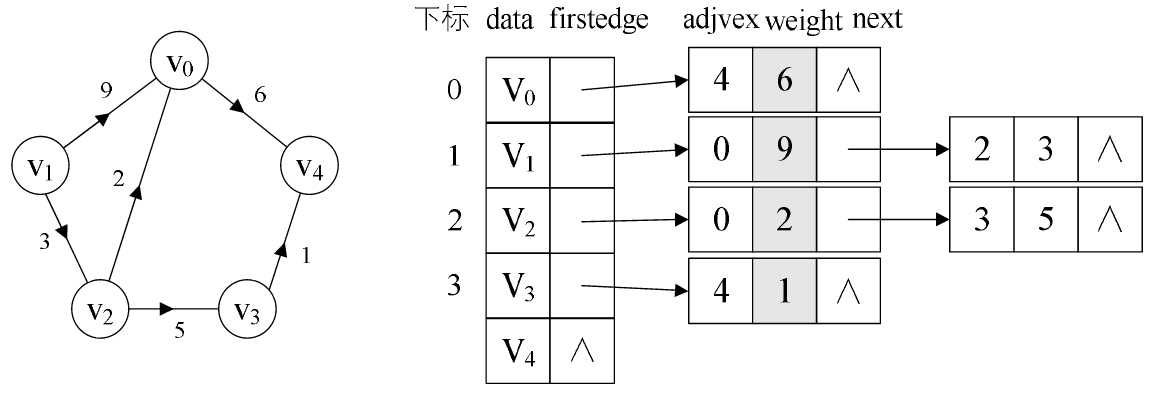
带权图的邻接链表:
/* * 无向图的邻接链表 */ #define MAXVEX 100 typedef char vtype; typedef int etype; /* 边表结点 */ typedef struct EdgeNode{ int adjvex; // 邻接点域,存储该顶点对应的下标 etype weight; // 用于存储权值,对于非带权图可以不需要 struct EdgeNode *next; // 链域,指向下一个邻接点 } EdgeNode; /* 顶点表结点 */ typedef struct VertexNode{ vtype data; // 顶点域,存储顶点信息 EdgeNode *firstedge; // 边表头指针 } VertexNode, AdjList[MAXVEX]; typedef struct{ AdjList adjList; int vertexes, edges; // 图中当前顶点数和边数 } GraphAdjList; /* 建立图的邻接表结构 */ void CreateALGraph(GraphAdjList *graph){ int i, j, k; EdgeNode *e; printf("输入顶点数和边数: "); scanf("%d,%d", &graph->vertexes, &graph->edges); /* 读入顶点信息,建立顶点表 */ for (i = 0; i < graph->vertexes; i++){ scanf(&graph->adjList[i].data); // 读入顶点信息 graph->adjList[i].firstedge = NULL; // 将边表置为空表 } /* 建立边表 */ for (k = 0; k < graph->edges; k++){ printf("输入边(vi,vj)上的顶点序号: "); scanf("%d,%d", &i, &j); e = (EdgeNode *)malloc(sizeof(EdgeNode)); // 向内存申请空间,生成边表结点 e->adjvex = j; // 邻接序号为j e->next = graph->adjList[i].firstedge; // 将e指针指向当前顶点指向的结点 graph->adjList[i].firstedge = e; // 将当前顶点的指针指向e e = (EdgeNode *)malloc(sizeof(EdgeNode)); // 向内存申请空间,生成边表结点 e->adjvex = i; // 邻接序号为i e->next = graph->adjList[j].firstedge; // 将e指针指向当前顶点指向的结点 graph->adjList[j].firstedge = e; // 将当前顶点的指针指向e } }
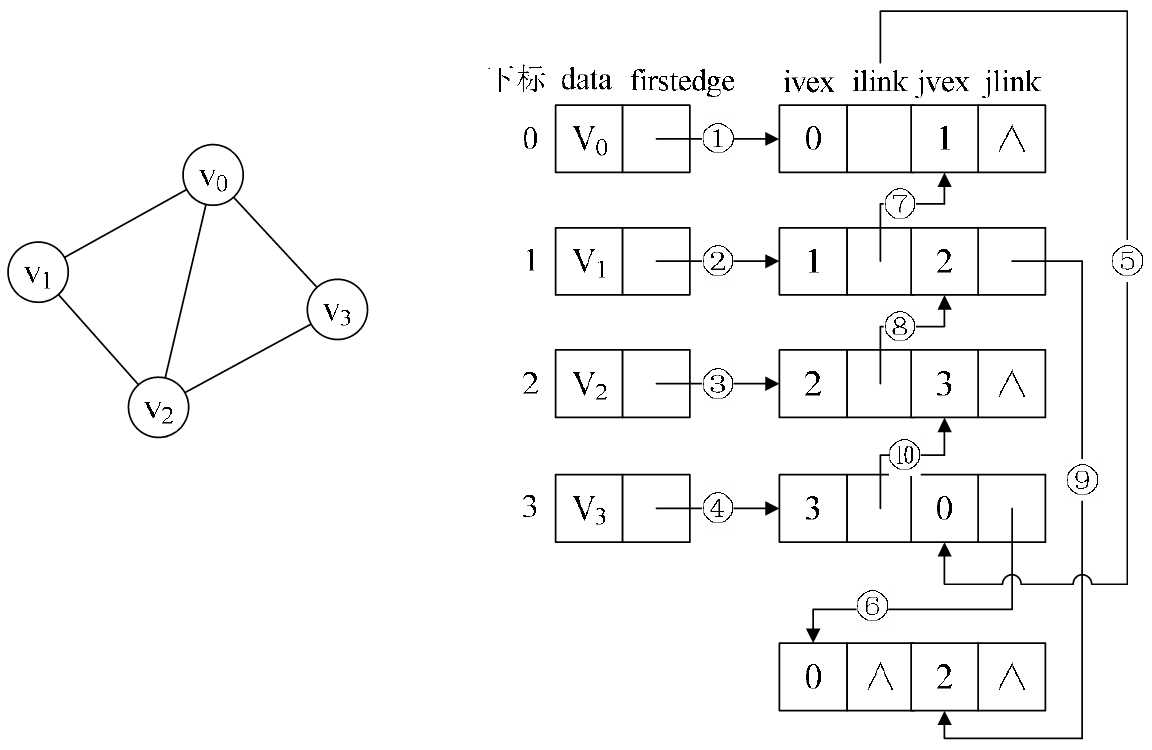
邻接多重表
邻接多重表是对无向图存储结构的优化,重新定义的边表结点结构如表所示

十字链表
十字链表是为了便于求得图中顶点的度(出度和入度)而提出来的,它是综合邻接表和逆邻接表形式的一种链式存储结构。
在十字链表存储结构中,有向图中的顶点的结构如下所示:
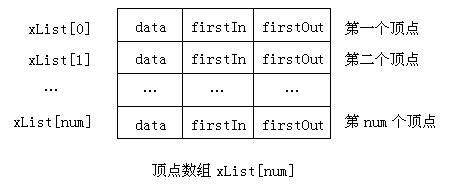
其中data表示顶点的具体数据信息,而firstIn则表示指向以该顶点为弧头的第一个弧节点。而firstOut则表示指向以该顶点为弧尾的第一个弧节点。为了表示有向图中所有的顶点,采用一个顶点数组存储每一个结点,如下图所示:
另外,在十字链表存储结构中,有向图中的每一条弧都有一个弧结点与之对应,具体的弧结点结构如下所示:
其中的tailVex表示该弧的弧尾顶点在顶点数组xList中的位置,headVex表示该弧的弧头顶点在顶点数组中的位置。hLink则表示指向弧头相同的下一条弧,tLink则表示指向弧尾相同的下一条弧。
从十字链表的数据结构来看,每一个顶点对应两个链表:以该顶点为弧尾的弧结点所组成的链表以及以该顶点为弧头的弧结点所组成的链表。
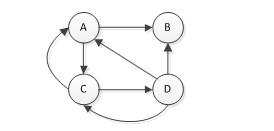
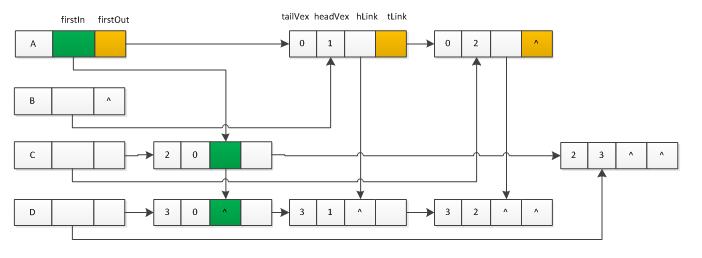
如下图所示的一个有向图:
其对应的顶点以及弧结点如下所示。拿结点A说明,该结点对应两个链表(绿色和黄色标记的)。绿色链表表示以结点A为弧头的弧组成的链表。黄色链表表示以结点A为弧尾的弧组成的链表。
#include <iostream> using namespace std; #define MAX_VERTEX_NUM 20 typedef int Status; typedef int infoType; typedef char vertexType; typedef struct arcBox { int tailVex, headVex; struct arcBox *hLink, *tLink; infoType *info; } arcBox; //弧结点 typedef struct vexNode { vertexType data; arcBox *firstIn, *firstOut; } vexNode; //顶点节点 typedef struct { vexNode xList[MAX_VERTEX_NUM]; int vexNum, arcNum; } OLGraph; //十字链 int locateVertex(OLGraph &G, vexNode node) { int index = -1; for (int i = 0; i < G.vexNum; i++) { if (node.data == G.xList[i].data) { index = i; break; } } return index; } void insertArcAction(OLGraph &G, int index1, int index2); Status insertArc(OLGraph &G, vexNode node1, vexNode node2); Status createDG(OLGraph &G, int vexNum, int arcNum) { G.vexNum = vexNum; G.arcNum = arcNum; for (int i = 0; i < G.vexNum; i++) { cin >> G.xList[i].data; G.xList[i].firstIn = NULL; G.xList[i].firstOut = NULL; }//初始化 for (int i = 0; i < G.arcNum; i++) { vexNode node1, node2; cout << "please input two nodes of " << i + 1 << "-th arc" << endl; cin >> node1.data >> node2.data; insertArc(G, node1, node2); } return 1; } Status printDG(OLGraph &G) { for (int i = 0; i < G.vexNum; i++) { arcBox *ptail = G.xList[i].firstOut; arcBox *phead = G.xList[i].firstIn; //打印以结点i为弧尾的链 cout << "以结点" << i << "为弧尾的链 " << G.xList[i].data; while (ptail) { cout << "-->" << "|" << ptail->tailVex << "|" << ptail->headVex; ptail = ptail-> tLink; } cout << "-->NULL" << endl; //打印以结点i为弧头的链 cout << "以结点" << i << "为弧头的链 " << G.xList[i].data; while (phead) { cout << "-->" << "|" << phead->tailVex << "|" << phead->headVex; phead = phead->hLink; } cout << "-->NULL" << endl; } return 1; } void insertArcAction(OLGraph &G, int index1, int index2) { arcBox* pArc = new arcBox[1]; pArc->tailVex = index1; pArc->headVex = index2; pArc->info = NULL; arcBox *ptail = G.xList[index1].firstOut; arcBox *phead = G.xList[index2].firstIn; if (!ptail) {pArc->tLink = NULL;} else {pArc->tLink = ptail;} if (!phead) {pArc->hLink = NULL;} else {pArc->hLink = phead;} G.xList[index1].firstOut = pArc;//链头部插入弧结点 G.xList[index2].firstIn = pArc; } Status insertArc(OLGraph &G, vexNode node1, vexNode node2) { int index1 = locateVertex(G, node1); int index2 = locateVertex(G, node2); insertArcAction(G, index1, index2); return 1; } Status insertNode(OLGraph &G, vexNode node) { G.xList[G.vexNum].data = node.data; G.xList[G.vexNum].firstIn = NULL; G.xList[G.vexNum].firstOut = NULL; G.vexNum = G.vexNum + 1; return 1; } Status deleteArc(OLGraph &G, vexNode node1, vexNode node2); Status deleteNode(OLGraph &G, vexNode node) { //删除结点后,该xList顶点数组中该结点后面的结点不前移,而只是将该被删除的结点的data设置成为一个较大的值 int index = locateVertex(G, node); for (int i = 0; i < G.vexNum; i++) { if (i == index) continue; else { deleteArc(G, G.xList[index], G.xList[i]);//删除以该结点为弧尾的弧 deleteArc(G, G.xList[i], G.xList[index]);//删除以该结点为弧头的弧 } } G.xList[index].data = '0';//置'0'表示该结点被删除 G.xList[index].firstIn = NULL; G.xList[index].firstOut = NULL; return 1; } void deleteOutArcAction(OLGraph &G, int index1, int index2) { arcBox *cur = G.xList[index1].firstOut; arcBox *pre = cur; int count = 0; if (!cur) return; else { while (cur) { count++; if (cur->headVex == index2) break; pre = cur; cur = cur->tLink; } } if (!cur) return;//该结点没有对应的弧 else if (count <= 1) G.xList[index1].firstOut = pre->tLink;//删除第一个弧结点 else pre->tLink = cur->tLink;//删除非第一个弧结点 } void deleteInArcAction(OLGraph &G, int index1, int index2) { arcBox *cur = G.xList[index2].firstIn; arcBox *pre = cur; int count = 0; if (!cur) return; else { while (cur) { count++; if (cur->tailVex == index1) break; pre = cur; cur = cur->hLink; } } if (!cur) return;//该结点没有对应的弧 else if (count <= 1) G.xList[index2].firstIn = pre->hLink; else pre->hLink = cur->hLink; } Status deleteArc(OLGraph &G, vexNode node1, vexNode node2) { //删除从结点1到结点2的弧(有方向) int index1 = locateVertex(G, node1); int index2 = locateVertex(G, node2); deleteOutArcAction(G, index1, index2);//删除两条链表里面的值 deleteInArcAction(G, index1, index2); return 1; } int main(int argc, _TCHAR* argv[]){ int vexNum = 4; int arcNum = 7; OLGraph G; cout << "Try to create a Orthogonal List of a graph..." << endl; createDG(G, vexNum, arcNum); cout << "Try to print the Orthogonal List of the very graph..." << endl; printDG(G); cout << "Try to insert a node into the graph..." << endl; vexNode node; cout << " please input the data of the node to insert:" << endl; cin >> node.data; insertNode(G, node); printDG(G); cout << "Try to insert a arc into the graph..." << endl; vexNode node1, node2; cout << " please choose two node:" << endl; cin >> node1.data >> node2.data; insertArc(G, node1, node2); printDG(G); cout << "Try to delete the arc between two nodes..." << endl; vexNode node3, node4; cout << " please choose a arc with specifing two nodes:" << endl; cin >> node3.data >> node4.data; deleteArc(G, node3, node4); printDG(G); cout << "Try to delete a node of the graph..." << endl; vexNode node5; cout << " please choose a node:" << endl; cin >> node5.data; deleteNode(G, node5); printDG(G); system("pause"); return 0; }