插入排序
插入排序的算法时间是O(N^2)。
int key = 0;
int length = s.length();
for (int i = 1; i < length; i++) {
key = ints[i];
int j = i-1;
while ( j>=0 && key < ints[j]) {
ints[j+1] = ints[j];
j--;
}
}
希尔排序
希尔排序是通过比较一个相距间隔内的元素进行排序。简单说来,n=ints.length,第一次排序将n=N/2作为第一次排序的增量,将ints数组每n=n/2个元素做一次间隔,对间隔内元素进行排序。以此类推,直到对n=1时进行排序。因此,希尔排序也叫缩减增量排序。
1.使用希尔增量时希尔排序的最坏情形运行时间为O(N^2)。
2.使用Hibbard增量的希尔排序的最坏情形运行时间为O(N^3/2)。
public static int[] pro(int[] ints) {
int n = ints.length;
int gap = n/2;
while(gap > 0){
for(int j = gap; j < n; j++){
int i=j;
while(i >= gap && ints[i-gap] > ints[i]){
int temp = ints[i-gap]+ints[i];
ints[i-gap] = temp-ints[i-gap];
ints[i] = temp-ints[i-gap];
i -= gap;
}
}
gap = gap/2;
}
return ints;
}
堆排序
堆排序的运行时间为O(NlogN)。我们在理解堆排序的思想需要明白大根堆和小根堆的概念。
对N个互异项的随机排列进行堆排序所用比较的平均次数为2NlogN-O(NloglogN)。
大根堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小根堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
1.将给定的数组按二叉树形式进行层序遍历。
2.然后从最后一个非叶子节点开始进行结构调整,原则是按照大根堆/小根堆的排列结构。节点调整顺序是从右至左,从下至上。
3.结构调整结束后,将根节点与最后一个叶子节点互换。将原根节点从堆中去除,放入数组中。
4.重新调整结构。
我们可以将上述操作带入到数组中。
a.将无需序列构建成一个堆,根据升序降序需求选择大根堆或小根堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
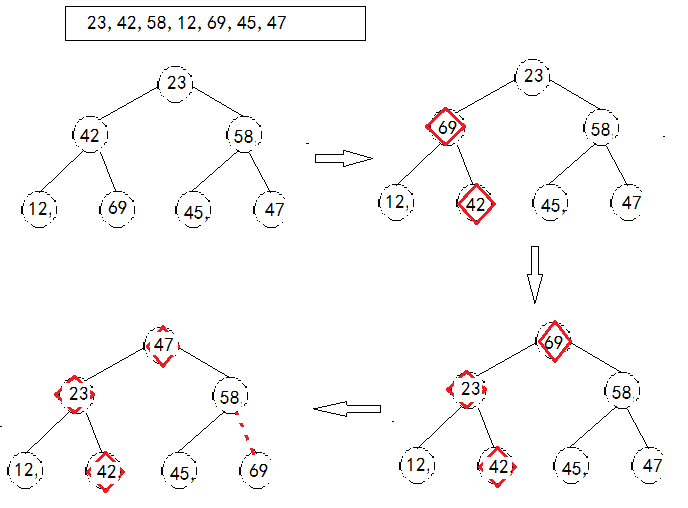
根据图示看一下。