冒泡:
public void bubbleSort(int[] arr){ for(int i=arr.length-1;i>0;i--){ for(int j=0;j<i;j++){ if(arr[j]>arr[j+1]){ swap(arr,j,j+1); } } } } //也可以 public void bubbleSort2(int[] arr){ for(int i=0;i<arr.length;i++){ for(int j=0;j<arr.length-1-i;j++){ if(arr[j]>arr[j+1]){ swap(arr,j,j+1); } } } }
插入:
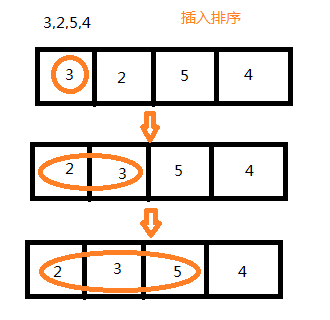
//插入排序 ({3},1,2)=>({1,3},2)=>({1,2,3}) public void insertSort(int[] arr){ //首先假设前方都排完了,我们排下一位 //第一个为有序,依次找 int insertIndex,insertVal; for (int i = 0; i < arr.length; i++) { insertVal=arr[i]; insertIndex=i-1; while (insertIndex>=0&&arr[insertIndex]>insertVal){ arr[insertIndex+1]=arr[insertIndex]; insertIndex--; } //前方全部后移之后,将该值插入到 arr[++insertIndex]=insertVal; } }
public void insertSort(int[] arr){ int temp; for (int i = 1; i < arr.length; i++) { for (int j = i; j > 0; j--) { if(arr[j]<arr[j-1]){ temp=arr[j]; arr[j]=arr[j-1]; arr[j-1]=temp; } } } }
希尔(移动):
//希尔排序(移动法) 具有增量的插入排序 public static void shellSort(int[] arr){ //增量+插入 int gap=arr.length/2; int insertIndex,insertVal; while (gap!=0){ for (int i = gap; i < arr.length; i++) { insertIndex=i-gap; insertVal=arr[i]; while (insertIndex>=0&&insertVal<arr[insertIndex]){ arr[insertIndex+gap]=arr[insertIndex]; insertIndex-=gap; } arr[insertIndex+gap]=insertVal; } gap=gap/2; } }
快速:
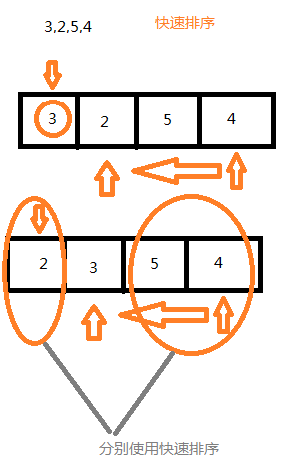
//快速排序 固定首位,先从右往左找小,再从左往右找大,重合时交换首位,再排基准的左和右 public static void quickSort(int[] arr){ quickSortFunc(arr,0,arr.length-1); } private static void quickSortFunc(int[] arr,int left,int right){ if(left>right){ return; } int l=left,r=right,base=arr[left]; while (l!=r){ //先从右往左找小,同时需要r指针不能小于l指针,之所以没等号,是因为如果本次满足的话,r--这样就小于l了,因此这里不可以加等于号 while (arr[r]>=base&&l<r){ r--; } //再从左往右找大 while (arr[l]<=base&&l<r){ l++; } ///交换 int temp=arr[l]; arr[l]=arr[r]; arr[r]=temp; } //此时说明l和r重合 即l==r arr[left]=arr[l]; arr[l]=base; //对于基准的左边排 quickSortFunc(arr,left,l-1); //对于基准的右边排 quickSortFunc(arr,l+1,right); }
归并:
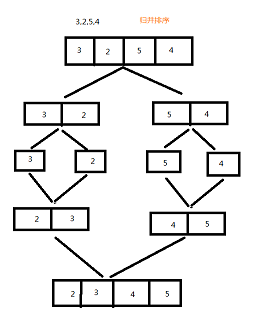
//归并排序 对半分解,然后(排序)拼接 public static void mergeSort(int[] arr){ int[] temp=new int[arr.length];//临时交换使用的数组 mergeSortFunc(arr,0,arr.length-1,temp); } private static void mergeSortFunc(int[] arr,int left,int right,int[] temp){ if(left>=right){//只有一个的时候 也不需要排序了 return; } int mid=(left+right)/2; mergeSortFunc(arr,left,mid,temp);//先排左边 mergeSortFunc(arr,mid+1,right,temp);//再排右边 //此时mid的左边和右边都是各自按照顺序排列,此时的思想和插入排序一样了 int l=mid,r=right,t=right; while (l>=left&&r>=mid+1){ if(arr[l]>arr[r]){ temp[t]=arr[l];//可以直接写成:temp[t--]=arr[l--]; 为了防止以后忘记,我写开,便于快速回忆 t--; l--; }else { temp[t--]=arr[r--]; } } //此时说明左边或者右边有一个已经全部填充完毕 //那么另一个直接按照顺序填充就去就好了 while (l>=left){ temp[t--]=arr[l--]; } while (r>=mid+1){ temp[t--]=arr[r--]; } //将本次调整的在temp记录的有顺序的值,赋值给arr对应位置 for (int i = left; i <= right; i++) { arr[i]=temp[i]; } }
桶排序:
(大顶堆:本节点的值要大于等于其左右子节点的值; 在升序排列中我们使用大顶堆,在降序排列中,我们是用小顶堆)
public static void bucketSort(int[] arr){ //第一次我们需要找倒数第一个非叶子节点,构造大顶堆(其索引位置在length/2-1),逐步由下往上构建大顶堆 for (int i = arr.length/2-1; i >=0; i--) { adjustHead(arr,i,arr.length); } //之后我们将根节点的元素与最后的元素交换,也就是和叶子节点交换, //因为除了根节点外,其余节点结构均未改变,因此我们只需要从根节点出发构建大顶堆即可了 for (int i=arr.length-1;i>=0;i--){ int temp=arr[0]; arr[0]=arr[i]; arr[i]=temp; adjustHead(arr,0,i); } } /** * 升序排,我们需要构建大顶堆,然后交换到最后 * @param arr 需要排序的数组 * @param i 非叶子节点在数组中的索引 * @param length 需要构建大顶堆的元素个数,length在逐渐减少 */ public static void adjustHead(int[] arr,int i,int length){ int temp=arr[i];//取出当前非叶子节点的值 //从当前非叶子节点开始,调整,一直调整到最下方 for (int j = i*2+1; j < length; j=j*2+1) { //判断左右节点那个值大 if(j+1<length&&arr[j]<arr[j+1]){ j++;//如果右节点的值较大,则j指向右节点,使用较大的值与temp比较 } if(arr[j]>temp){ arr[i]=arr[j];//让当前非叶子节点的值,赋值为这个最大的值 i=j;//同时i指向j当前位置,因为这个节点改变了嘛,因此我还需要判断当前这个节点是否满足大顶堆 }else { break;//如果当前非叶子节点的值最大,那么它已经是一个大顶堆了,我们不要再动了 } } arr[i]=temp; }
堆排序:
推荐网址(非常清晰):https://www.cnblogs.com/chengxiao/p/6129630.html
public static void sort(int[] arr) { //1.构建大顶堆 for (int i = arr.length / 2 - 1; i >= 0; i--) { //从第一个非叶子结点从下至上,从右至左调整结构 adjustHeap(arr, i, arr.length); } //2.调整堆结构+交换堆顶元素与末尾元素 for (int j = arr.length - 1; j > 0; j--) { swap(arr, 0, j);//将堆顶元素与末尾元素进行交换 adjustHeap(arr, 0, j);//重新对堆进行调整 } } /** * 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上) * * @param arr * @param i * @param length * 也就是要把当前位置的值放包含当前的值和子节点的值 */ public static void adjustHeap(int[] arr, int i, int length) { int temp = arr[i];//先取出当前元素i for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {//从i结点的左子结点开始,也就是2i+1处开始 if (k + 1 < length && arr[k] < arr[k + 1]) {//如果左子结点小于右子结点,k指向右子结点 k++; } if (arr[k] > temp) {//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换) arr[i] = arr[k]; i = k; } else { break; } } arr[i] = temp;//将temp值放到最终的位置 } /** * 交换元素 * * @param arr * @param a * @param b */ public static void swap(int[] arr, int a, int b) { int temp = arr[a]; arr[a] = arr[b]; arr[b] = temp; }
//递归版的更好理解(B站视频讲解很清楚哦) public static void adjustHead(int[] arr,int i,int length){ if(i>=length)return; int leftChildIndex=2*i+1; int rightChildIndex=2*i+2; int maxIndex=i; if(leftChildIndex < length && arr[leftChildIndex]> arr[maxIndex]){ maxIndex = leftChildIndex; } if(rightChildIndex < length && arr[rightChildIndex]> arr[maxIndex]){ maxIndex = rightChildIndex; } if(maxIndex!=i){ swap(arr,i,maxIndex); adjustHead(arr,maxIndex,length); } }