【Algorithm】堆排序

　　堆是一种完全二叉树结构，并且其满足一种性质：父节点存储值大于（或小于）其孩子节点存储值，分别称为大顶堆、小顶堆。堆一般采用数组进行存储（从下标为0开始）。则父节点位置为i，那么其左孩子为2*i + 1，右孩子为2*i + 2。

一. 算法描述

　　堆排序主要分为两个过程：

• 建堆：先使长度为N数组形成一个N个节点组成的大顶堆（从第N/2个元素开始）
• 交换：然后将堆顶元素与末尾元素交换
• 筛选：再对N-1长的堆调整为大顶堆（从堆顶元素开始）；反复进行，直到堆节点数为1时，结束堆排序。

　　例子：给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。

　　1）构建大顶堆

　　首先，根据该数组元素构建一个完全二叉树，得到

　　然后，需要构造初始堆，则从最后一个非叶节点（N/2）开始调整，调整过程如下：

　　这样就得到了初始堆。即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

　　2）交换

　　3）筛选

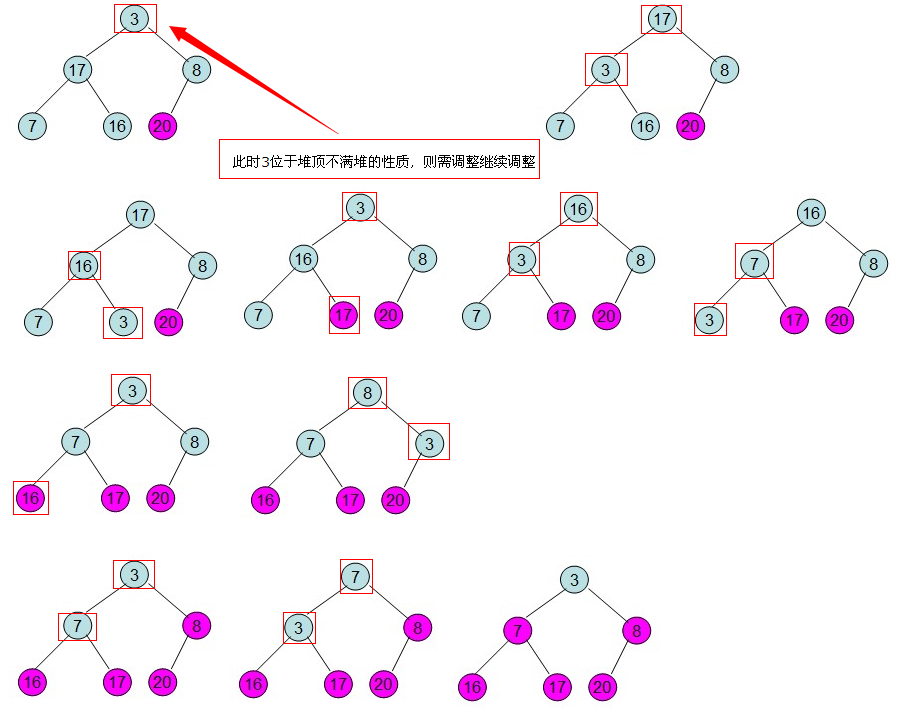
 　　这样整个区间便已经有序了。

　　从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。

二. 算法实现

#include<stdio.h>
void HeapSort(int array[],int length);
void HeapAdjust(int array[],int i,int nLength);
void main(){
    int intArr[] = {8,3,6,4,2,9,5,4,1,7};
    int n = sizeof(intArr) / sizeof(intArr[0]); // 计算整型数组的长度
    int i;
    HeapSort(intArr, n);

    // 打印输出结果
    for(i = 0; i < n; i++){
        printf("%d ",intArr[i]);
    }
    printf("
");

}

/*
* 堆排序算法, 分为三步：
*    第一步：建堆；
*    第二步：堆顶与最后一个元素交换；
*    第三步：重新调整堆(从堆顶开始)，之后重复二三步
*/
void HeapSort(int array[],int length){
    int tmp, i ;
    //调整序列的前半部分元素，调整完之后第一个元素是序列的最大的元素
    //length/2 - 1是最后一个非叶节点，此处"/"为整除
    for(i = length/2 - 1; i >= 0; --i){
        HeapAdjust(array,i,length);
    }
    //从最后一个元素开始对序列进行调整，不断的缩小调整的范围直到第一个元素
    for(i = length-1; i > 0; --i){
        //把第一个元素和当前的最后一个元素交换，
        //保证当前的最后一个位置的元素都是在现在的这个序列之中最大的
        ///Swap(&array[0],&array[i]);
        tmp = array[i];
        array[i] = array[0];
        array[0] = tmp;
        //不断缩小调整heap的范围，每一次调整完毕保证第一个元素是当前序列的最大值
        HeapAdjust(array, 0, i);
    }
}


/*
* array是待调整的堆数组，i是待调整的数组元素的位置，nlength是数组的长度
* 本函数功能是：根据数组array构建大根堆
*/
void HeapAdjust(int array[],int i,int nLength){
    int nChild;
    int nTemp;
    for(; 2*i+1 < nLength; i = nChild){
        //左孩子
        nChild = 2 * i + 1;
        //得到子结点中较大的结点
        if(nChild < nLength-1 && array[nChild+1] > array[nChild]){
            ++nChild;
        }
        //如果较大的子结点大于父结点那么把较大的子结点往上移动，替换它的父结点
        if(array[i] < array[nChild]){
            nTemp = array[i];
            array[i] = array[nChild];
            array[nChild] = nTemp;
        }else{
        //否则退出循环
            break;
        }
    }
}

三. 算法分析

• 平均时间复杂度：O(nlog2n)
• 空间复杂度：O(1) （用于交换数据） 
• 稳定性：不稳定
• 由于建初始堆所需的比较次数较多，所以堆排序不适宜于记录数较少的文件。

参考资料

　　[1] http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html

　　[2] http://zh.wikipedia.org/zh-cn/%E5%A0%86%E7%A9%8D%E6%8E%92%E5%BA%8F

　　[3] http://blog.csdn.net/cjf_iceking/article/details/7928254