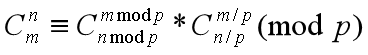组合数问题一:
给定n组询问,每组询问给定两个整数a,b,请你输出
的值。
1≤n≤10000,
1≤b≤a≤2000
模板题链接:组合数一
问题特点:数据组数较多,a,b的范围较小,且要求对一个定值取模。
解决方法:杨辉三角
因为a,b范围非常小,直接利用杨辉三角打表即可。
代码实现:
#include <cstdio> #include <algorithm> #include <iostream> using namespace std; const int N = 2010, mod = 1e9+7; int s[N][N]; void start() { s[0][0]=1; for(int i=1;i<=N-5;i++) for(int j=1;j<=i;j++) s[i][j]=(s[i-1][j]+s[i-1][j-1])%mod; } int main() { start(); int n;scanf("%d",&n); for(int i=1;i<=n;i++) { int a,b; scanf("%d%d",&a,&b); printf("%d ",s[a+1][b+1]); } return 0; }
组合数问题二
给定n组询问,每组询问给定两个整数a,b,请你输出
的值。
1≤n≤10000,
1≤b≤a≤105
模板题链接:组合数二
问题特点:数据组数较多,a,b范围较大,且要求对一个定值取模。
解决方法:乘法逆元
利用乘法逆元将a/b mod p转化成a*b-1 mod p。
然后将阶乘与阶乘的逆元分别打表即可。
递推式:
① n! = (n-1)! * n
② n!-1 = (n-1)!-1 * np-2
②的证明:
(n-1)!-1 = (n-1)!p-2
(n-1)!p-2 * np-2 = n!p-2
代码实现:
#include <iostream> #include <cstdio> using namespace std; typedef long long ll; const int N = 100000+10, mod = 1e9 + 7; int jc[N],ny[N]; int qmi(int a,int k,int p) { int res=1%p; while(k) { if(k&1)res=(ll)res*a%p; a=(ll)a*a%p; k>>=1; } return res; } void start() { jc[0]=1;ny[0]=1; for(int i=1;i<=N-5;i++) { jc[i]=(ll)jc[i-1]*i%mod; ny[i]=(ll)ny[i-1]*qmi(i,mod-2,mod)%mod; } } int main() { start(); int n;scanf("%d",&n); for(int i=1;i<=n;i++) { int a,b;scanf("%d%d",&a,&b); int ans=(ll)jc[a]*ny[b]%mod*ny[a-b]%mod; printf("%d ",ans%mod); } return 0; }
组合数问题三
给定n组询问,每组询问给定三个整数a,b,p,其中p是质数,请你输出
的值
1≤n≤20,
1≤b≤a≤1018,
1≤p≤105
模板题链接:组合数三
问题特点:数据组数较少,a,b范围很大,p的值非定值。
解决方法:Lucas定理
若p是质数,则对于任意整数1≤m≤n,有:
相当于是把n和m表示成p进制数,对p进制下的每一位分别计算组合数,最后再乘起来。
利用Lucas定理将目标组合数递归分解,直到m和n小于p为止。
然后对于每个分解出来的m和n的范围均在p以内的组合数,就可以放心地根据组合数的定义直接求解。
当然,对于每一步计算过程,都需要对p取模,遇到除法的利用快速幂转化成乘法逆元即可。
代码实现:
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> using namespace std; typedef long long ll; int p; //用的次数比较多的变量,一般设置的变量名比较短,且一般设成全局变量 int qmi(int a,int k) { int res=1; while(k) { if(k&1) { res=(ll)res * a % p; } a=(ll)a * a % p; k>>=1; } return res; } int C(int a,int b) { if(a<b)return 0; int res=1; for(int i=a,j=1;j<=b;i--,j++) { res = (ll)res * i % p; res = (ll)res * qmi(j,p-2)%p; } return res; } int lucas(ll a,ll b) { if(a<p&&b<p)return C(a,b); { return (ll)C(a%p,b%p)*lucas(a/p,b/p)%p; } } int main() { int n;scanf("%d",&n); while(n--) { ll a,b; scanf("%lld%lld%d",&a,&b,&p); //scanf是c的语法,cin是c++的语法,函数内部自带& printf("%d ",lucas(a,b)); } return 0; }
组合数问题四
输入a,b,求
的值。
注意结果可能很大,需要使用高精度计算。
1≤b≤a≤5000
模板题链接:组合数四
问题特点:只有一组数据,a,b取值不大,但没有要求取模。
解决方法:高精度
题目没有要求取模,就没办法在过程中保证数据的大小,只能暴力高精度。
根据组合数的定义,可得:
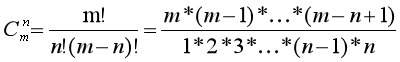
在循环过程中一边乘一边除即可,这样便只需要写两个函数:高精度乘低精度,高精度除以低精度。
代码实现:
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> using namespace std; struct largeint{ int len; int num[10010]; }; largeint lar_mult(largeint a,int b) { for(int i=1;i<=a.len;i++)a.num[i]*=b; for(int i=1;i<=a.len;i++) { a.num[i+1]+=a.num[i]/10; a.num[i]%=10; } if(a.num[a.len+1]>0)a.len++; while(a.num[a.len]>9) { a.len++; a.num[a.len]+=a.num[a.len-1]/10; a.num[a.len-1]%=10; } while(a.num[a.len]==0&&a.len>1)a.len--; return a; } largeint lar_div(largeint a,int b) { for(int i=a.len;i>=1;i--) { if(i>1)a.num[i-1]+=(a.num[i]%b)*10; a.num[i]/=b; } while(a.num[a.len]==0&&a.len>1)a.len--; return a; } void print(largeint n) { for(int i=n.len;i>=1;i--) printf("%d",n.num[i]); printf(" "); return; } int main() { int a,b; scanf("%d%d",&a,&b); largeint res; res.num[1]=1;res.len=1; for(int i=a,j=1;j<=b;i--,j++) { res=lar_mult(res,i); res=lar_div(res,j); } print(res); return 0; }