DS博客作业02--栈和队列

0.PTA得分截图：

1.本周学习总结

1.1栈相关知识

--栈：（stack）又名堆栈。是只能能在表尾进行增删操作的线性表，特点为先进后出。是数据暂时存储的地方。分为顺序栈和链式栈。
--栈的基本操作：

（1)进栈：if栈满即top==MaxSize-1时作错误处理else S(++top)=X(X为进栈新元素）
（2）出栈：if栈空即top<0时作错误处理else X=S(--top)(出栈后的元素赋给X）
--栈的STL容器的简单用法：

#include<stack>
stack<int>sta;
判断栈的大小：sta.size();
入栈：sta.push(X);
判断栈是否为空：sta.empty();
出栈：sta.pop();

--栈的简单应用：根据栈的特性，栈可用于求解像括号配对，迷宫求解，表达式求值等类似的题目
以括号配对为例：
思路：
（1）碰到左括号时将其入栈
（2）碰到右括号时先判断堆栈是否为空，再判断该括号是否与栈顶元素匹配
（3）最后要判断堆栈是否为空
代码实现：

#include<iostream>
using namespace std;
int IsMatch(char p, char q);
int main()
{
	char str[1000];
	char stack[100];
	int top = -1;

	scanf("%s", str);
	for (int i = 0; str[i] != ''; i++)
	{
		if (str[i] == '(' || str[i] == '[' || str[i] == '{')
		{
			stack[++top] = str[i];
		}
		if (str[i] == ')' || str[i] == ']' || str[i] == '}')
		{
			if (top == -1)
			{
				cout << "no";
				return 0;
			}
			else
			{
				if (IsMatch(stack[top],str[i]))
					top--;
				else	
				{
					cout << stack[top] << endl;
					cout << "no";
					return 0;
				}
			}
		}
	}
	if (top == -1)
		cout << "yes";
	else
		cout << stack[top] << endl << "no";

	return 0;
}
int IsMatch(char p, char q)
{
	if (p == '(' && q == ')')
		return 1;
	if (p == '[' && q == ']')
		return 1;
	if (p == '{' && q == '}')
		return 1;
	return 0;
}

1.2队列相关知识

--队列（queue）：和堆栈一样时一种特殊的线性表，它特殊在只允许在表头进行删除操作、表尾进行插入操作，特点为先进先出，也有顺序式和链式之分，除此之外，队列还有为了充分利用其存储空间的循环队列的形式。
--队列的基本操作：

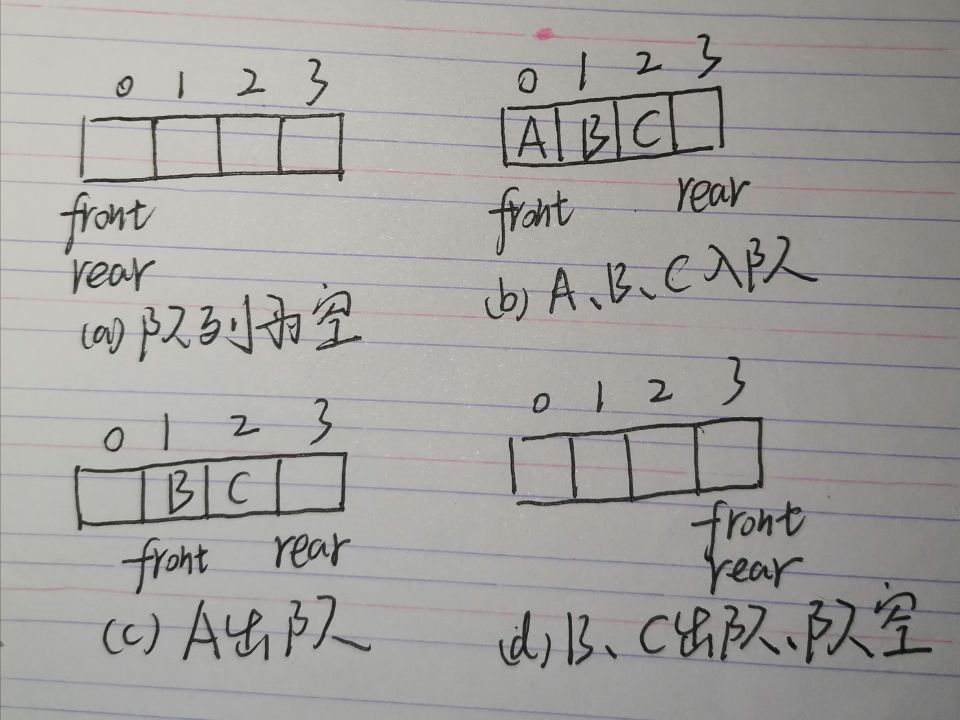
（1）入队：if队满即rear == Max Size-1时作错误处理else Q（++rear）=X（X为入队元素）
（2）出队：if队空即front == rear时作错误处理else X=Q（++front）（出队后的元素赋给X）
注：循环队列的队满需和一般队列做不同处理其一种处理为：（rear+1）%MaxSize==front
--队列的STL容器的简单用法：

#include <queue>
queue<int> q; //定义队列
q.empty()://判断队列是否为空
q.push(1); //入队
q.pop(); //出队
int v=q.front(); //得到队首的值
int s=q.size(); //得到队列里元素个数

--队列的简单应用：报数问题、排队问题等
以7-7 银行业务队列简单模拟为例
思路：
（1）依次存入数据到A、B两个队列
（2）当满足A.size>=2&&B.size>=1时按顺序进行出队操作
（3）最后将A、B队中的剩余元素按顺序输出
代码实现：

#include<iostream>
using namespace std;
int main()
{
	int queuea[10000], queueb[10000];
	int fronta = 0, frontb = 0;
	int reara = 0, rearb = 0;
	int n, num;

	cin >> n;
	while (n--)
	{	
		cin >> num;
		if ((reara - fronta >= 2) && (rearb - frontb >= 1))
		{
			if ((reara - fronta == 2) && (rearb - frontb == 1) && n == 0)
			{
				cout << queuea[++fronta] << " ", cout << queuea[++fronta] << " ";
				cout << queueb[++frontb];
			}
			else
			{
				cout << queuea[++fronta] << " ", cout << queuea[++fronta] << " ";
				cout << queueb[++frontb] << " ";
			}
		}
		if (num % 2 == 0)
			queueb[++rearb] = num;
		else
			queuea[++reara] = num;
	}
	while (reara - fronta > 1)
		cout << queuea[++fronta] << " ";
	if(reara - fronta > 0)
	{
		if (rearb - frontb == 0)
			cout << queuea[++fronta];
		else
			cout << queuea[++fronta] << " ";
	}
	while (rearb - frontb > 1)
		cout << queueb[++frontb] << " ";
	if(rearb - frontb > 0)
		cout << queueb[++frontb];
}

1.2对栈和队列的学习体会

通过栈和队列的学习让我了解到日常生活中普通现象背后的数据结构以及对此类问题的一般解法

2PTA实验作业

2.1 7-3 jmu-ds-符号配对 (15分)

2.1.1代码截图：

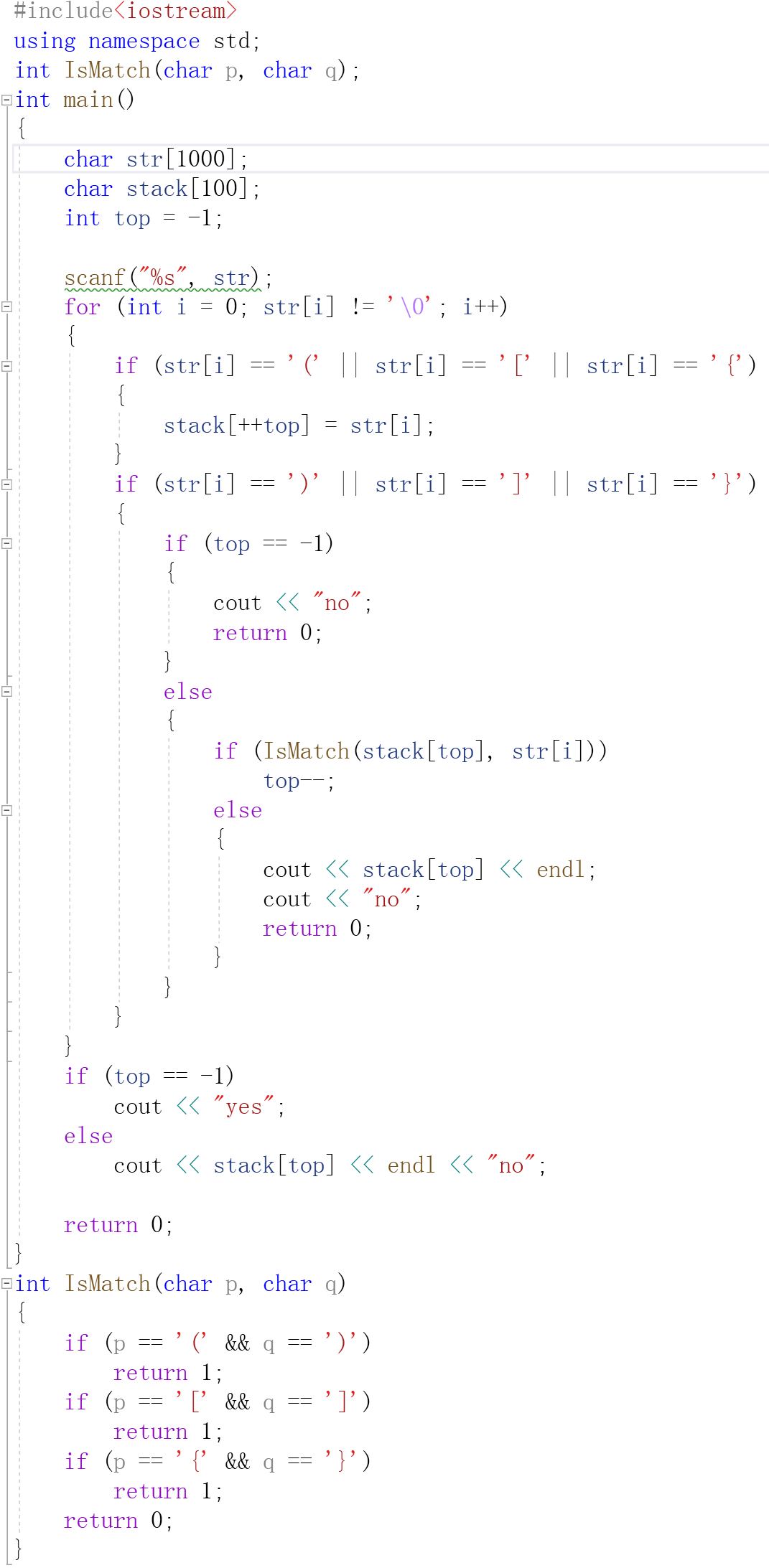
2.1.2提交列表及说明：

（1）编译器选错了

2.2 7-6 jmu-报数游戏 (15分)

2.2.1代码截图：

2.2.2提交列表及说明：

（1）该题所用方法为链式队列

3.阅读代码

3.1 题目及解题代码

3.1.1 该题的设计思路
该题和通常意义的银行排队问题是一个类型的，主要在设置优先级、大量变量的定义、以及采用何种数据结构等方面来考察学生。当然也少不了阅读理解。。
3.1.2 该题的伪代码
其思路和队列问题类似：

while（操作数！=0）
{
若操作数k==1//进行入队操作
if（优先级P较低） 排在队尾
else 排在队首
k==2//进行高优先级出队操作
{将优先级最高元素出队}
k==3//进行低优先级出队操作
{将优先级最低元素出队}
}

3.1.3 运行结果

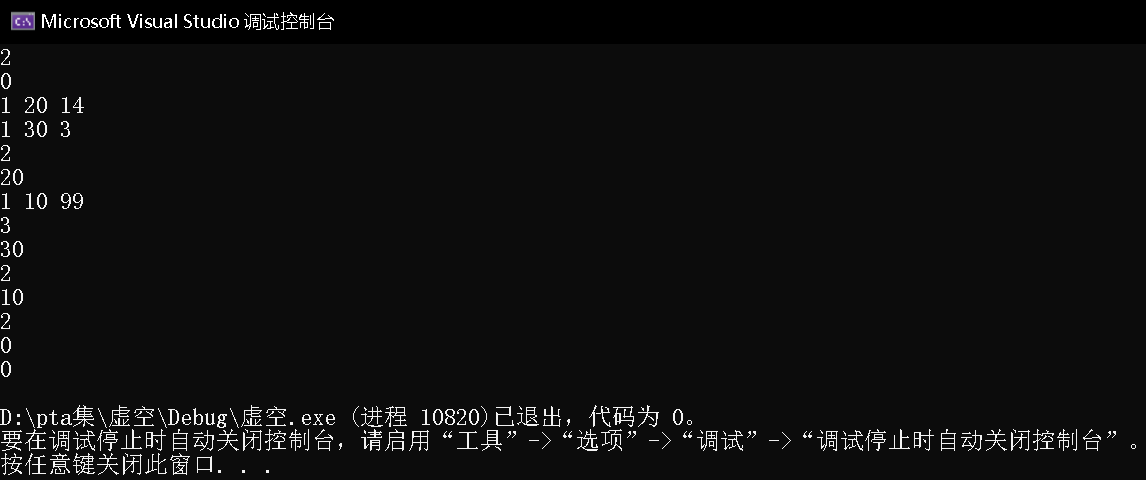
3.1.4分析该题目解题优势及难点
解题优势主要在于题目本身并非难题，一旦分析好数据间的关系就很容易想到对应的解题思路。而其难点在于题目中变量的定义与应用，可以看到在该题的解题代码中题者使用了全局变量和全局数组来处理数据关系，使得数据间的关系豁然开朗，变量得到充分利用，也是因此其时间空间复杂度都很小，是成熟规范的好代码。