结对项目， 四则运算

这个作业属于哪个课程	软件工程
这个作业要求在哪里	作业要求
这个作业的目标	编写一个生成一定要求（数量、数值）四则运算的程序； 进行性能分析、回归测试； 把代码上传到GitHub

成员学号姓名、GitHub地址：邱志城3118005380、麦倬豪3118005377、GitHub地址

PSP2.1	Personal Software Process Stages	预估耗时(分钟）	实际耗时（分钟）
Planning	计划	60	240
Estimate	估计这个任务需要多少时间	20	30
Development	开发	1000	1500
Analysis	需求分析 (包括学习新技术)	180	360
Design Spec	生成设计文档	20	60
Design Review	设计复审	60	96
Coding Standard	代码规范 (为目前的开发制定合适的规范)	30	90
Design	具体设计	100	150
Coding	具体编码	700	1050
Code Review	代码复审	200	300
Test	测试（自我测试，修改代码，提交修改）	60	90
Reporting	报告	60	90
Test Repor	测试报告	20	30
Size Measurement	计算工作量	5	10
Postmortem & Process Improvement Plan	事后总结, 并提出过程改进计划	5	10
Total	总计	1260	2000

各模块介绍

项目使用python语言
包括main.py, run_cmd.py, myfra.py, get_exp.py, test.py五个模块

• myfra.py
  • 分数类MyFra，类属性有int_part（整数部分）、up（分子）、down（分母），类方法有__init__、reduction、ran_fra、change_fra、show_fra五个类方法；
    • self.init()：初始化分数对象，在方法末尾调用self.reduction()
    • self.reduction()：约分，并把假分数化为带分数，调用了自定义函数max_com_factor()用于生成分子和分母的最大公因数
    • self.ran_fra()：随机改变分数对象的三个属性，以达到随机生成分数的作用。调用了python自带的随机整数生成函数random.randint()
    • self.change_fra()：把分数转化成假分数（使int_part = 0）方便之后计算函数的使用
    • self.show()：返回分数的字符串表示，方便式子和答案写入文件中
  • 外置运算函数max_com_factor()、int_to_fra()、addition()、subtraction()、multiplication()、division()六个函数
• run_cmd.py
  • get_argv()：调用sys.argv()、getopt.getopt()，（按选项）接收命令行参数并返回
  • run()：调用get_exp.py的两个函数，生成算式、答案，写入文件，调用get_argv()，根据其返回值运行
• test.py，单元测试
• get_exp.py
  • get_exp()，生成算式以及计算答案，并以列表的形式返回。调用了myfra.py里的分数（MyFra）类以及各个函数
• main.py，主模块，生成最终结果

关键部分代码展示

• 分数类MyFra

由于作业要求使用整数和真分数（带分数）进行题目生成和计算，而我们找不到现成的能随机生成一定范围内分数的python函数，所以就设计了一个类来统一运算数（整数和分数），并且设计了一个类方法self.ran_fra()来随机生成一定范围内的数（通过创建对象然后按范围随机修改对象的属性）。代码如下：

class MyFra:

# 初始化分数类
def __init__(self, int_part=0, up=0, down=1):
    self.int_part = int_part
    self.up = up
    self.down = down

    self.reduction()

# 随机生成一个分数
def ran_fra(self, max_fra):
    self.int_part = random.randint(0, max_fra)

    if self.int_part == max_fra:
        self.down = 1
        self.up = 0
    else:
        self.down = random.randint(1, max_fra)
        self.up = random.randint(0, self.down)
    # print(self.int_part, self.down, self.up)

    self.reduction()

# 对分数进行约分，调用了max_com_factor()函数（辗转相除法）；自动转化为带分数
def reduction(self):
    if self.up != 0:
        mcf = max_com_factor(self.up, self.down)
        self.up = self.up // mcf
        self.down = self.down // mcf
        # print(self.show_fra())
        if self.up * self.down < 0:
            self.int_part = -1  # 表示不支持负分数
        else:
            self.int_part = self.int_part + self.up // self.down
            self.up = self.up % self.down

    else:
        self.down = 1

    return self.show_fra()

# 将真分数变成假分数并返回
def change_fra(self):
    ch_fra = MyFra()
    ch_fra.up = self.up + self.int_part * self.down
    ch_fra.down = self.down
    return ch_fra

# 将分数转化为字符串返回，分三种情况
def show_fra(self):
    if self.up == 0:
        return str(self.int_part)
    if self.up != 0 and self.int_part == 0:
        return "{}/{}".format(self.up, self.down)
    else:
        return "{}'{}/{}".format(self.int_part, self.up, self.down)

• get_exp()

实现原理：
首先，由于需要生成大量题目，于是考虑使用while循环来生成表达式;同时，因为设计需求中需要在最后输出表达式以及运算结果，于是便在函数中定义了两个空列表，并以字符串的形式将表达式以及运算结果分别存储在两个列表中，输出时只需遍历列表即可
以下为部分代码：

  def get_exp(rag_max, exp_num):
         rag_max = rag_max - 1 # 传递输入的范围参数，生成的随机数不超过rag_max - 1
         i = 1                  
         expression_all = []   # 用于存储表达式   
         answer_all = []       # 用于存储运算结果
         operator = ['+', '-', '×', '÷']  # 构造了一个列表，存储了'+'、'-'、'×'、'÷'四个符号，并利用python的ramdom.randint()函数来随机选择生成的运算符
         while i <= exp_num:

由于设计需求中要求表达式中不超过三个运算符，于是便选用除3取余的方法来生成表达式：

  if i % 3 == 1 # 当i满足除3余数为1时，生成只含一个运算符的表达式
  if i % 3 == 2 # 当i满足除3余数为2时，生成只含两个运算符的表达式
  if i % 3 == 3 # 当i能被3整除时，生成只含三个运算符的表达式

匹配完i % 3的结果之后，便构造字典，字典中指明了对应位置的操作数是什么、对应位置的运算符是什么，并存储了运算的结果
比如说i % 3 == 1 时：

  # 利用自己写的分数类中的ran_fra()方法，生成分数对象后即利用该方法生成操作数
  a = myfra.MyFra() 
  b = myfra.MyFra()
  a.ran_fra(rag_max)
  b.ran_fra(rag_max)
  
  # 随机生成运算符
  op_1 = operator[random.randint(0, 3)]      
  expression = {
                'ser': i,             # 题目序号
                'num_1': a,           # 位于第一个位置的操作数对象
                'num_2': b,           # 位于第二个位置的操作数对象
                'operator_1': op_1,   # 位于第一个位置的运算符
                'num_len': 2,         # 操作数数量
                'op_len': 1,          # 运算符数量
                'answer': '0'         # 未进行运算时，初始答案均设置为0
                 }

然后，对操作数，调用相应的分数类方法进行运算，并将正确的运算结果赋予到字典的'answer'当中。由于代码过长不便全部展示，这里截取部分代码：

       if expression['operator_1'] == '+':
            myfra.addition(expression['num_1'], expression['num_2'])
            expression['answer'] = myfra.addition(expression['num_1'], expression['num_2']).show_fra()
        elif expression['operator_1'] == '-':
            while (myfra.subtraction(expression['num_1'], expression['num_2']).int_part < 0 or
                   myfra.subtraction(expression['num_1'], expression['num_2']).up < 0):
                expression['num_2'].ran_fra(rag_max)
            expression['answer'] = myfra.subtraction(expression['num_1'], expression['num_2']).show_fra()
        elif expression['operator_1'] == '×':
            myfra.multiplication(expression['num_1'], expression['num_2'])
            expression['answer'] = myfra.multiplication(expression['num_1'], expression['num_2']).show_fra()
        elif expression['operator_1'] == '÷':
            while expression['num_2'].int_part == 0 and expression['num_2'].up == 0:
                expression['num_2'].ran_fra(rag_max)
            expression['answer'] = myfra.divide(expression['num_1'], expression['num_2']).show_fra()

要注意的是，进行运算时，我们使用了穷举的方法，列举了不超过三个运算符的所有可能运算符位置，并结合操作数一一进行类函数调用运算

运算结束后，将表达式以及运算结果写入之前生成的用于存储表达式和运算结果的列表当中：

  # 将字典中的序号、对应操作数和运算符拼接成一个字符串，存入列表中
  expression_all.append(str(expression['ser']) + '、' + expression['num_1'].show_fra() + ' ' +
                              str(expression['operator_1']) + ' ' + expression['num_2'].show_fra())
  # 将字典中的序号和运算结果拼接成一个字符串，存入列表中
  answer_all.append(str(expression['ser']) + '、' + expression['answer'])

当while循环结束时，表达式列表以及运算结果列表即存储了生成的所有题目以及答案。函数返回的两个列表即可用于后续输出。

测试运行

• 单元测试代码：

import unittest
import myfra
import get_exp
class MyTestCase(unittest.TestCase):

def test_mcf(self):
    self.assertEqual(myfra.max_com_factor(21, 14), 7)
    self.assertEqual(myfra.max_com_factor(15, 25), 5)
    self.assertEqual(myfra.max_com_factor(66, 55), 11)
    self.assertEqual(myfra.max_com_factor(27, 18), 9)
    self.assertEqual(myfra.max_com_factor(64, 56), 8)

def test_reduction(self):  # 在MyFra对象生成之后自动调用reduction()方法，所以这里直接用show_fra()方法
    test_1 = myfra.MyFra(0, 12, 34)
    test_2 = myfra.MyFra(0, 34, 12)
    self.assertEqual(test_1.show_fra(), "6/17")
    self.assertEqual(test_2.show_fra(), "2'5/6")
    self.assertEqual(myfra.MyFra(1, 13, 12).show_fra(), "2'1/12")
    self.assertEqual(myfra.MyFra(12, 0, 12).show_fra(), "12")
    self.assertEqual(myfra.MyFra().show_fra(), "0")

def test_add(self):
    test_1 = myfra.MyFra(12, 3, 4)
    test_2 = myfra.MyFra(12, 3, 5)
    self.assertEqual(myfra.addition(12, 13).show_fra(), "25")
    self.assertEqual(myfra.addition(12, test_1).show_fra(), "24'3/4")
    self.assertEqual(myfra.addition(test_2, 13).show_fra(), "25'3/5")
    self.assertEqual(myfra.addition(test_1, test_2).show_fra(), "25'7/20")

def test_sub(self):
    test_1 = myfra.MyFra(0, 1, 12)
    test_2 = myfra.MyFra(1, 3, 5)
    self.assertEqual(myfra.subtraction(test_1, test_2).int_part, -1)
    self.assertEqual(myfra.subtraction(1, test_1).show_fra(), "11/12")
    self.assertEqual(myfra.subtraction(test_2, 1).show_fra(), "3/5")
    self.assertEqual(myfra.subtraction(test_2, test_1).show_fra(), "1'31/60")

def test_div(self):
    test_1 = myfra.MyFra(0, 1, 12)
    test_2 = myfra.MyFra(1, 3, 5)
    self.assertEqual(myfra.divide(test_1, 2).show_fra(), "1/24")
    self.assertEqual(myfra.divide(2, test_1).show_fra(), "24")
    self.assertEqual(myfra.divide(test_1, test_2).show_fra(), "5/96")

def test_exp(self):
    exercises, answers = get_exp.get_exp(10, 10)
    self.assertEqual(len(exercises), 10)

if name == 'main':
unittest.main()

• 单元测试运行结果：

单元测试使用pycharm自带的unittest，self.assertEqual(avgr1， avgr2)中，若两个参数不相同则会报错，图中运行通过，故所选测试样例是能让addition()、subtraction()、divide()、max_com_factor()、get_exp()、MyFra的类方法reduction()正确运行的

• main.py运行结果：

  • 命令行输入-r和-n参数，运行脚本：

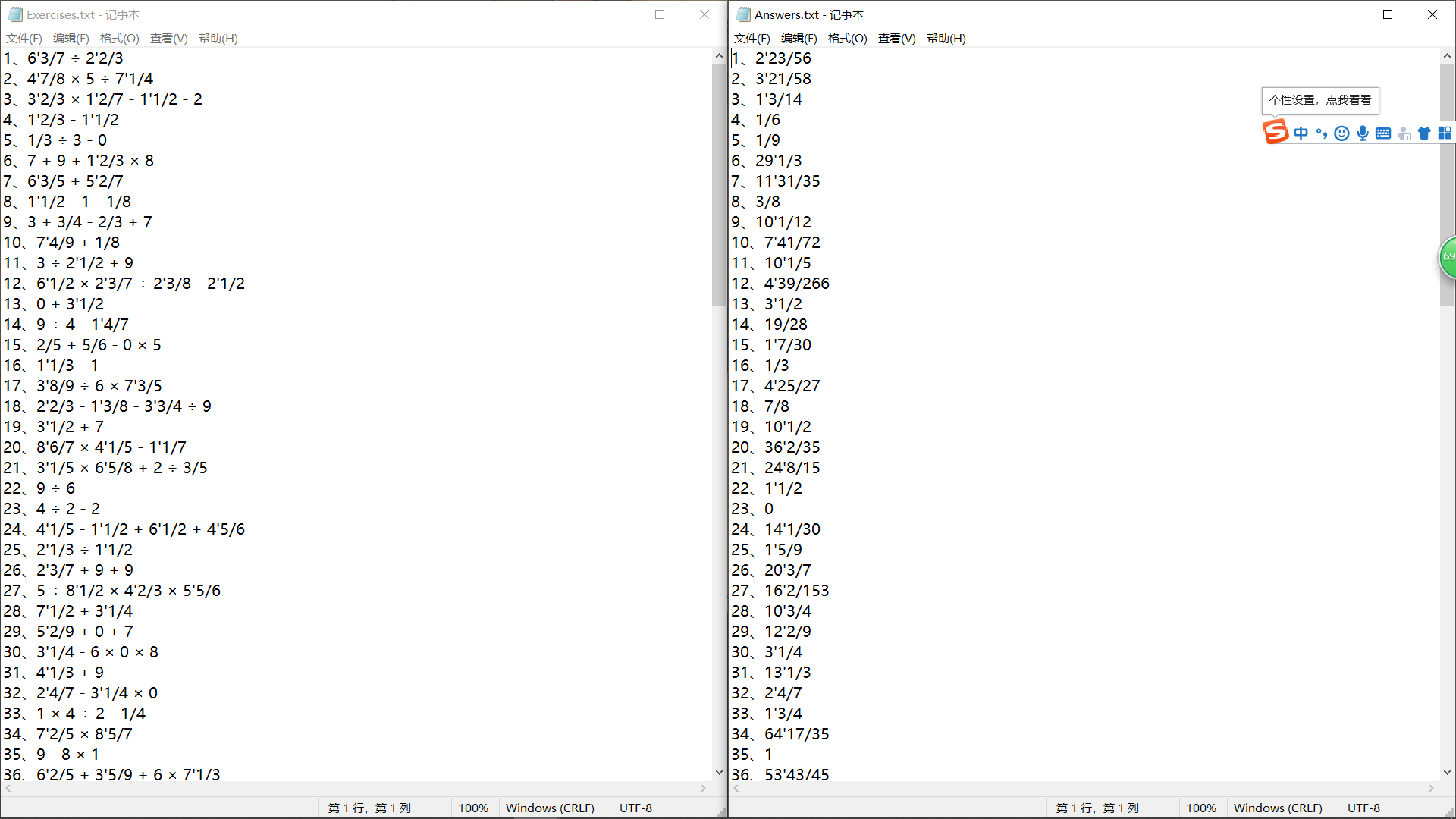
- 文件的写入结果：

心得与体会

• 邱志城：我觉得我们这次结对项目主要的问题在于对完成所需时间的估计不够到位，，而且对自己的实力估计错误，在寻找解决方法上耗费了太多时间，导致太晚开始。这次的项目我使用了以前未用过的Pycharm。里面自动进行的代码规范化让我改掉了很多以前编程的坏习惯，让我认识到代码规范化的重要性。

• 麦倬豪：这次的结对编程，极大地锻炼了我的团队合作能力以及我的编程能力，也揭露了我的不足之处，比如说编程不规范、数据结构不熟练等。这让我有了接下来的努力方向。同时，这也让我充分明白了沟通交流的重要性。在编程的初期，由于我没有很好地和我的队友进行充分的沟通，导致我自己做了大量的无用功，白白地浪费了很多时间。虽然之后及时地与队友进行了沟通，但流逝的时间已无法弥补。以后再进行团队合作类的项目时，我会更加地注重与队友的沟通交流。