luogu P2664 树上游戏 |点分治

题目描述

lrb有一棵树，树的每个节点有个颜色。给一个长度为n的颜色序列，定义s(i,j) 为i 到j 的颜色数量。以及

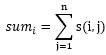
现在他想让你求出所有的sum[i]

输入格式

第一行为一个整数n，表示树节点的数量

第二行为n个整数，分别表示n个节点的颜色c[1],c[2]……c[n]

接下来n-1行，每行为两个整数x,y，表示x和y之间有一条边

输出格式

输出n行，第i行为sum[i]

---

点分治

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
using namespace std;
#define ll long long
#define pb push_back
#define MAX 100100
inline int read()
{
    int x=0;bool t=false;char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')t=true,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
    return t?-x:x;
}
vector<int> E[MAX];
int n,c[MAX];ll ans[MAX];
int mx,Size,rt,sz[MAX];
bool vis[MAX];
void Getroot(int u,int ff)
{
    sz[u]=1;int ret=0;
    for(int v:E[u])
    {
        if(v==ff||vis[v])continue;
        Getroot(v,u);sz[u]+=sz[v];
        ret=max(ret,sz[v]);
    }
    ret=max(ret,Size-sz[u]);
    if(ret<mx)mx=ret,rt=u;
}
int cnt[MAX];ll num[MAX],sum;
void dfs(int u,int ff,int opt)
{
    if(!cnt[c[u]]++)num[c[u]]+=opt*sz[u],sum+=opt*sz[u];
    for(int v:E[u])if(v!=ff&&!vis[v])dfs(v,u,opt);
    --cnt[c[u]];
}
void dfs(int u,int ff)
{
    if(!cnt[c[u]]++)sum+=Size-num[c[u]];
    ans[u]+=sum;
    for(int v:E[u])if(v!=ff&&!vis[v])dfs(v,u);
    if(!--cnt[c[u]])sum-=Size-num[c[u]];
}
void Divide(int u)
{
    vis[u]=true;Getroot(u,0);
    dfs(u,0,1);ans[u]+=sum;Size=sz[u];
    for(int v:E[u])
    {
        if(vis[v])continue;
        num[c[u]]-=sz[v];sum-=sz[v];Size-=sz[v];
        cnt[c[u]]=1;dfs(v,u,-1);cnt[c[u]]=0;
        dfs(v,u);
        cnt[c[u]]=1;dfs(v,u,1);cnt[c[u]]=0;
        num[c[u]]+=sz[v];sum+=sz[v];Size+=sz[v];
    }
    dfs(u,0,-1);
    for(int v:E[u])
    {
        if(vis[v])continue;
        mx=Size=sz[v];Getroot(v,u);
        Divide(rt);
    }
}
int main()
{
    n=read();
    for(int i=1;i<=n;++i)c[i]=read();
    for(int i=1,u,v;i<n;++i)u=read(),v=read(),E[u].pb(v),E[v].pb(u);
    mx=Size=n;Getroot(1,0);
    Divide(rt);
    for(int i=1;i<=n;++i)printf("%lld
",ans[i]);
    return 0;
    }