什么是线段树
线段树,是一种二叉搜索树。它将一段区间划分为若干单位区间,每一个节点都储存着一个区间。它功能强大,支持区间求和,区间最大值,区间修改,单点修改等操作。
线段树的思想和分治思想很相像。
线段树的每一个节点都储存着一段区间[L…R]的信息,其中叶子节点L=R。它的大致思想是:将一段大区间平均地划分成2个小区间,每一个小区间都再平均分成2个更小区间……以此类推,直到每一个区间的L等于R(这样这个区间仅包含一个节点的信息,无法被划分)。通过对这些区间进行修改、查询,来实现对大区间的修改、查询。
线段树的原理及实现
线段树主要是把一段大区间平均地划分成两段小区间进行维护,再用小区间的值来更新大区间。这样既能保证正确性,又能使时间保持在log级别(因为这棵线段树是平衡的)。
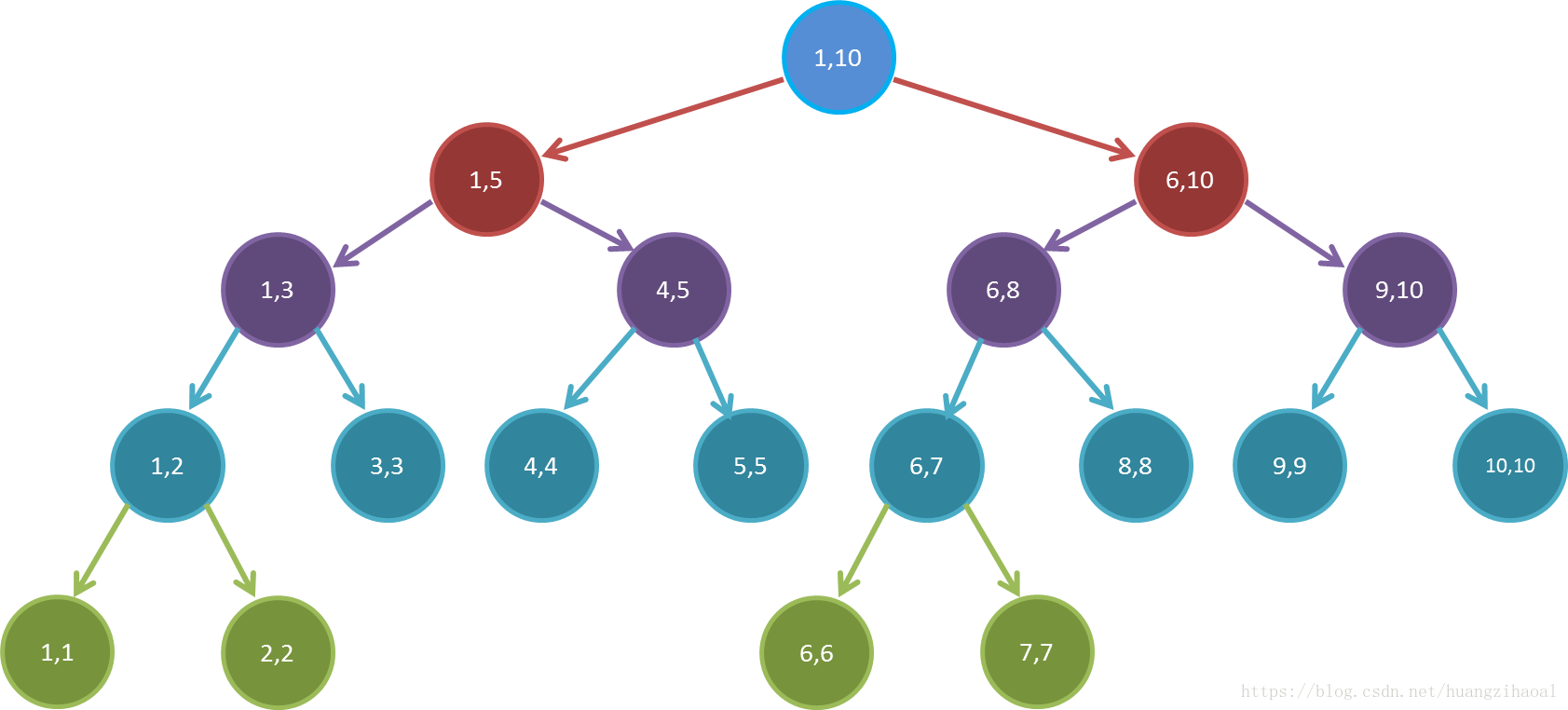
下图就是一棵[1…10]的线段树的分解过程(相同颜色的节点在同一层)
注:以下代码都是在区间求和的情况下
储存方式
通常用的都是堆式储存法,即编号为k的节点的左儿子编号为k∗2 k*2k∗2,右儿子编号为k∗2+1 k*2+1k∗2+1,
通常,每一个线段树上的节点储存的都是这几个变量:区间左边界,区间右边界,区间的答案(这里为区间元素之和)
下面是线段树的定义:
1 //maxn表示有多少个点 2 const int maxn=50000; 3 struct node 4 { 5 //l表示左边,r表示右边; 6 int l,r; 7 //sum表示该线段的值 8 int sum; 9 //lazy为懒惰标记,能够优化区间修改的速度 10 int lazy; 11 }no[maxn*4];//为保证树的成功建立,节点数一般是点数的4倍以上
初始化
常见的做法是遍历整棵线段树,给每一个节点赋值,注意要递归到线段树的叶节点才结束。
1 //k表示当前节点的编号,l表示当前区间的左边界,r表示当前区间的右边界 2 void build(int k,int l,int r) 3 { 4 no[k].l=l; 5 no[k].r=r; 6 //如果递归到最低点 7 if(l==r) 8 { 9 //赋值并记录该点对应的节点编号,number存放的是对应点的值 10 no[k].sum=number[l]; 11 //pa数组存放根点对应的节点数,这样可以简化单点修改的方法 12 pa[l]=k; 13 return ; 14 } 15 //对半分 16 int mid=(l+r)/2; 17 //递归到左线段 18 build(k*2,l,mid); 19 //递归到右线段 20 build(k*2+1,mid+1,r); 21 //用左右线段的值更新该线段的值 22 no[k].sum=no[k*2].sum+no[k*2+1].sum; 23 }
单点修改
包含两种情况:第一种是值的加减,在这种情况下我们可以额外开一个数组pa[]用于记录每个点对应的根节点的编号,这样我们在修改时直接修改树上了个根节点的值,然后在递归回树的最高处,沿途把数据同样处理一下即可,例如addvalue()方法
第二种情况是值的改变,就是把它的值全变成另一个值,这种情况下我们能迭代加二分判断的方法,从数的顶点开始查找,根据目标点所在树商店区间一步一步缩小范围,直到找到那个点,然后修改值并在回溯时把沿途经过的素有点的值都改一下,例如changevalue()方法
1 //单点值加减 2 //调用方法:addvalue(pa[i],x) 3 //功能:从根点i对应的节点k对值进行加减,并往上调用维护树 4 //k表示节点数的编号,x为正数表示加,x为负数表示减 5 void addvalue(int k,int x) 6 { 7 no[k].sum +=x; 8 //如果该节点不是最高的节点则往上递归 9 if(k!=1) 10 { 11 addvalue(k/2,x); 12 } 13 } 14 15 //单点值修改 16 //调用方法:changevalue(1,x,y) 17 //功能:从节点数1开始查找树,直到遇到根点x,并将值修改为y,并且维护树的数据 18 //k表示节点数的编号,要把节点x的sum值变成y 19 void changevalue(int k,int x,int y) 20 { 21 if(no[k].l==no[k].r) 22 { 23 no[k].sum=y; 24 return ; 25 } 26 int mid =(no[k].l+no[k].r)/2; 27 //判断根点x在哪个区间内 28 //递归到左线段 29 if(x<=mid) 30 { 31 changevalue(k*2,x,y); 32 } 33 else//递归到右线段 34 { 35 changevalue(k*2+1,x,y); 36 } 37 //用左右线段的值更新该线段的值,维护树 38 no[k].sum=max(no[k*2].sum,no[k*2+1].sum); 39 }
下传标记
下传标记时为了简化区间操作而提出的概念,正常情况下区间修改时找到所有在这个区间内的点,然后修改值并且回溯路径,但这样很容易超时,因此有一个想法是在查找树时,如果找到了这个区间的子区间时,可以先改这个子区间的值,并标记下来,而不需要再往下查找了,这样时间就会节省很多,因此标记就这么产生了,下传标记是指当你找到子区间并标记子区间时,由于在这个子区间内的所有元素都要被修改,因此不需要在查找了,只需从这个值子区间开始往下递归,改变所有的值,并删除这一层的标记将标记载往下传。大概实现就是这样子的,首先根据区间操作的不同,下传标记也分为了几类,但大体构架差不多,只是核心代码不也一样,具体情况见代码
1 //传递标记 2 //调用方法:pushdown(k) 3 //功能:将节点数为k的数据往下传递 4 //k表示节点数的编号, 5 void pushdown(int k) 6 { 7 //当前节点不是最低层时 8 if(no[k].l!=no[k].r) 9 { 10 11 //区间修改为值修改时的代码 12 { 13 //更新子节点的值 14 no[k*2].sum=(no[k*2].r-no[k*2].l+1)*no[k].lazy; 15 no[k*2+1].sum=(no[k*2+1].r-no[k*2+1].l+1)*no[k].lazy; 16 //更新子节点的标记 17 no[k*2].lazy=no[k*2+1].lazy=no[k].lazy; 18 } 19 20 //区间修改为值加减时的代码 21 { 22 //更新子节点的值 23 no[k*2].sum+=(no[k*2].r-no[k].l+1)*no[k].lazy; 24 no[k*2+1].sum+=(no[k*2+1].r-no[k*2+1].l+1)*no[k].lazy; 25 //更新子节点的标记 26 no[k*2].lazy+=no[k].lazy; 27 no[k*2+1].lazy+=no[k].lazy; 28 } 29 30 //区间修改为值覆盖问题的代码 31 { 32 //更新子节点的值 33 no[k*2].sum=no[k*2+1].sum=no[k].lazy; 34 //更新子节点的标记 35 no[k*2].lazy=no[k*2+1].lazy=no[k].lazy; 36 } 37 38 } 39 //清除当前节点的标记 40 no[k].lazy=0; 41 }
区间修改
区间修改和单点修改对应也包括两种情况:第一种是区间值的加减,它的思路是在从树的定点开始往下搜索,如果遇到在目标区间内的在区间或点,将这个节点的值加上它(r-l+1)*x的值,并标记,然后再在回溯是维护一下路径就可以。
第二种就是区间的更改,它的思路和区间值的加减相同,不同的是在遇到目标区间内的子区间或点时,这个节点的值要变为(r-l+1)*x,而不是加上,同样要表记这个节点,且回溯时一样要维护路径。
1 //区间修改包括值修改和值加减 2 //调用方法:sectionchange(k,l,r,x) 3 //功能:从节点1开始查找树,修改区间[l,r]内的值,将值变为x或值加上x。并且维护线段树 4 //k表示节点数的编号,l,r,表示目标区间,x表示要变成的值或要加减的值 5 void sectionchange(int k,int l,int r,int x) 6 { 7 //检查并下传标记 8 if(no[k].lazy) 9 { 10 pushdown(k); 11 } 12 //到对应层时更新值与标记 13 if(no[k].l==l&&no[k].r==r) 14 { 15 //区间修改为值修改时的代码 16 { 17 no[k].sum=(no[k].r-no[k].l+1)*x; 18 no[k].lazy=x; 19 } 20 //区间修改为值加减时的代码 21 { 22 no[k].sum+=(r-l+1)*x; 23 no[k].lazy+=x; 24 } 25 return ; 26 } 27 //取中值 28 int mid=(no[k].l+no[k].r)/2; 29 if(r<=mid) 30 { 31 //如果被修改区间完全在左区间 32 sectionchange(k*2,l,r,x); 33 } 34 else if(l>mid) 35 { 36 //如果被修改区间完全在右区间 37 sectionchange(k*2+1,l,r,x); 38 } 39 else 40 { 41 //如果都不在,就要把修改区间分解成两块,分别往左右区间递归 42 sectionchange(k*2,l,mid,x); 43 sectionchange(k*2+1,mid+1,r,x); 44 } 45 //更新当前节点的值,维护线段树 46 no[k].sum=no[k*2].sum+no[k*2+1].sum; 47 }
区间覆盖
区间覆盖和区间值修改类似,但是它不适用于区间求和的问题,适合区间标记的问题,依此也要改一点代码,也能用到下传标记。具体情况将代码。
1 //区间覆盖 2 //调用方法:sectionchange(k,l,r,x) 3 //功能:从节点1开始查找树,将区间[l,r]内的值都打上值为x的标记 4 //k表示节点数的编号,l,r,表示目标区间,x表示要覆盖的值 5 void sectioncover(int k,int l,int r,int x) 6 { 7 //检查并下传标记 8 if(no[k].lazy) 9 { 10 pushdown(k); 11 } 12 //到最底层时更新值与标记 13 if(no[k].l==l&&no[k].r==r) 14 { 15 no[k].sum=x; 16 no[k].lazy=x; 17 return ; 18 } 19 //取中值 20 int mid=(no[k].l+no[k].r)/2; 21 22 if(r<=mid) 23 { 24 //如果被修改区间完全在左区间 25 sectioncover(k*2,l,r,x); 26 } 27 else if(l>mid) 28 { 29 //如果被修改区间完全在右区间 30 sectioncover(k*2+1,l,r,x); 31 } 32 else 33 { 34 //如果都不在,就要把修改区间分解成两块,分别往左右区间递归 35 sectioncover(k*2,l,mid,x); 36 sectioncover(k*2+1,mid+1,r,x); 37 } 38 //更新当前节点的值,min纯属我个人需要也可以写其他的 39 no[k].sum=min(no[k*2].sum,no[k*2+1].sum); 40 }
区间求和
从树的顶点往下搜索,如果遇到目标区间内的子区间或点时,返回对应节点的值即可,过程种没有修改因此不需要维护,但如果下传标记还是要有的。
1 //区间求和 2 //调用方法:query(k,l,r) 3 //功能:从节点1开始查找树,求区间[l,r]内所有数的和 4 //k表示当前节点的编号,l表示当前区间的左边界,r表示当前区间的右边界 5 int query(int k,int l,int r) 6 { 7 //如果当前区间就是询问区间,完全重合,那么显然可以直接返回 8 if(no[k].l==l&&no[k].r==r) 9 { 10 return no[k].sum; 11 } 12 //如果当前节点被打上了懒惰标记,那么就把这个标记下传, 13 if(no[k].lazy) 14 { 15 pushdown(k); 16 } 17 //取中值 18 int mid = (no[k].l+no[k].r)/2; 19 //如果询问区间包含在左子区间中 20 if(r<=mid) 21 { 22 return query(k*2,l,r); 23 } 24 else if(l>mid)//如果询问区间包含在右子区间中 25 { 26 return query(k*2+1,l,r); 27 } 28 else//如果询问区间跨越两个子区间 29 { 30 return query(k*2,l,mid)+query(k*2+1,mid+1,r); 31 } 32 }
区间求最值
由于求最值的反向大概相同因此我把求最小值和最大值和到一块了,但不影响使用。首先求最值问题在初始化时就会把节点的值换成它的最值,因此它的代码没有什么难度,和区间求和的思想基本相同,不顾它返回的时最值,而且在目标区间涉及两个子区间时返回的是两个子区间的最值。
1 //区间锥子 2 //调用方法:querymaxin(k,l,r,falg) 3 //功能:从节点1开始查找树,查找位于区间[l,r]中点的值的最大值和最小值, 4 //flag用于表示最大和最小,为1时表示求最小值,为0时表示求最大值 5 //k表示节点数的编号,l,r,表示目标区间,flag决定时求最大值还是最小值 6 int querymaxin(int k,int l,int r,int flag) 7 { 8 //到对应层时返回值 9 if(no[k].l==l&&no[k].r==r) 10 { 11 if(flag==1) 12 { 13 //返回最小 14 return no[k].mi; 15 } 16 else 17 { 18 //返回最大 19 return no[k].ma; 20 } 21 } 22 //取中值 23 int mid=(no[k].l+no[k].r)/2; 24 //如果询问区间包含在左子区间中 25 if(r<=mid) 26 { 27 return querymaxin(k*2,l,r,flag); 28 } 29 else if(l>mid)//如果询问区间包含在右子区间中 30 { 31 return querymaxin(k*2+1,l,r,flag); 32 } 33 else//如果询问区间跨越两个子区间 34 { 35 if(flag==1) 36 { //返回两个子区间的最小值 37 return min(querymaxin(k*2,l,mid,flag),querymaxin(k*2+1,mid+1,r,flag)); 38 } 39 else 40 { //返回两个子区间的最大值 41 return max(querymaxin(k*2,l,mid,flag),querymaxin(k*2+1,mid+1,r,flag)); 42 } 43 } 44 }
总结:目前我个人的题量,线段树在有下几个方面的应用:
1:在整个数组中,通过加减或修改任意区间的值,最后求指定区间的和
2:在一个画板中,按照顺序上色,问最后能看见几种颜色或几个颜色块
3:给定一排相连的树,然后去掉几个树,问与第i个相连的树有几个,