完备事件组
设 Ω 为试验E的样本空间,B1, B2, …, Bn 为E的一组事件。若
Bi ∩ Bj = Φ (i ≠ j 且 i, j =1, 2, …n)
B1 U B2 U … U Bn = Ω
则称B1, B2, …, Bn 为样本空间 Ω 的完备事件组的一个划分。
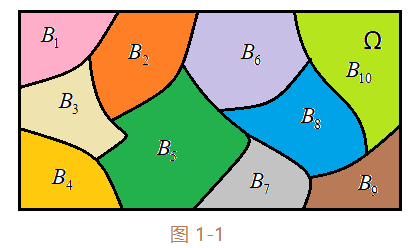
注:上图就是对一个样本空间的划分且每个划分单元两两不相容。
全概率的概念
设A1,A2,…,An 是一组互不相容的事件,形成样本空间的一个分割(每个试验结果必使其中一个事件发生).
又假定对每个i,P(Ai) > 0.则对任何事件B,下列公式成立
P(B) = P(A1 ∩ B) + P(A2 ∩ B) + … + P(An ∩ B)
= P(A1)P(B|A1) + … + P(An)P(B|An)

上图解释:
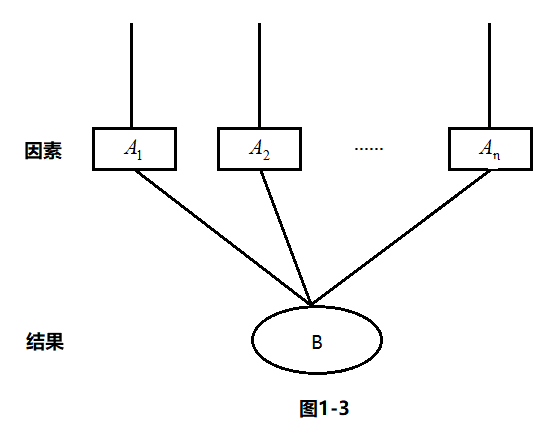
上面这n中因素都可以导致事件B发生,所以事件B发生的可能性为 P(A1)P(B|A1) + … + P(An)P(B|An),这又叫正向概率
贝叶斯公式
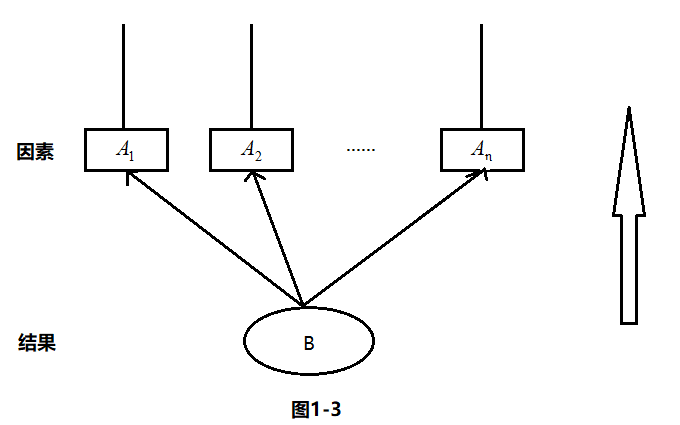
对上图稍加改变,就成了我们的贝叶斯公式。换句话说,就是已知结果,求那个因素导致其发生的概率。
贝叶斯概念
设A1,A2,…,An 是一组互不相容的事件,形成样本空间的一个分割(每个试验结果必使其中一个事件发生).
又假定对每个i,P(Ai) > 0.则对任何事件B
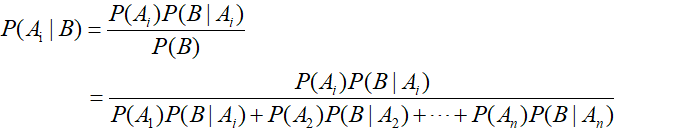
贝叶斯是用来进行因果推。有许多“原因”可以造成某一个结果。现在假设我们观察到了某一个结果,希望推断造
成这个结果的原因。现在设事件A1,A2,…,An 是原因,B代表由原因引起的结果。P(B|Ai) 表示在因果模型中
由“原因”Ai造成结果B出现的概率。
当观察结果 B 的时候,我们希望反推结果 B 是由原因 Ai 造成的概率 P( Ai | B ). P( Ai | B )为由于代表新近得到
的信息B之后Ai出现的概率,称之为后验概率,而原来的P(Ai)就称为先验概率。