以下是本蒟蒻从百度百科上整理的一些比较重要的矩阵的一些基本的定义:
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:

基本运算
- 加法

减法

数乘
矩阵乘法
定义:
设A为(m*n)的矩阵,B为(p*n)的矩阵,那么称(m*n)的矩阵C为矩阵A与B的乘积,记作(C=AB)
注意:两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。

根据定义所以说这样的矩阵也是可以相乘的:
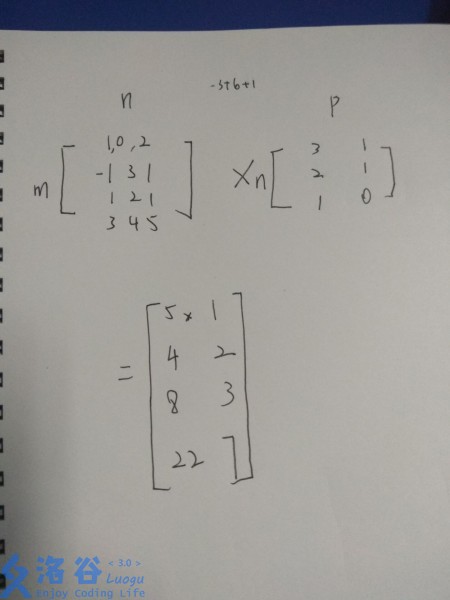
然后我们在来科普几个矩阵的乘法性质:
首先先要明白的是,(C=AB),然后你下面的才能看得懂!
矩阵的乘法满足以下运算律:
结合律:((AB)C=A(BC))
左分配律:((A+B)C=AC+BC)
右分配律:(C(A+B)=CA+CB)
矩阵乘法不满足交换律!!!
有了以上这些矩阵的基本知识,我想我们应该可以来讲解一下矩阵快速幂这个东西了。
哇!一直调不出来绝望!
