前言
本文讲解如何使用R语言中e1071包中的SVM函数进行分类操作,并以一个关于鸢尾花分类的实例演示具体分类步骤。
分析总体流程
1. 载入并了解数据集;
2. 对数据集进行训练并生成模型;
3. 在此模型之上调用测试数据集进行分类测试;
4. 查看分类结果;
5. 进行各种参数的调试并重复2-4直至分类的结果让人满意为止。
参数调整策略
综合来说,主要有以下四个方面需要调整:
1. 选择合适的核函数;
2. 调整误分点容忍度参数cost;
3. 调整各核函数的参数;
4. 调整各样本的权重。
其中,对于特征比较多的情况一般用非线性核,比如高斯核。高斯核的特点是参数多,需要不断调试参数才能理想的效果。而线性核没什么参数可设置,一般适用于特征比较少的情况。
关于各核函数的参数,则一般是通过试探法来确定。最好可以将不同样本权重模型,不同核函数参数下的分类准确率做成一张可视化报表,以便于方案确定。
关于3的选择,一般可以通过MDS的可视化图,看有哪几个分类是纠缠不清的,然后就加大这两个分类的样本权重。
鸢尾花分类分析 - 使用支持向量机(SVM)
1. 安装SVM分析所需包:e1071
2. 载入并了解数据集:

可以看出,这个数据集比较理想化,避免了繁琐的数据预处理过程,非常适合作为案例讲解。
3. 建立SVM模型:

这个模型变量相当于是训练库,下面查看该模型的信息:
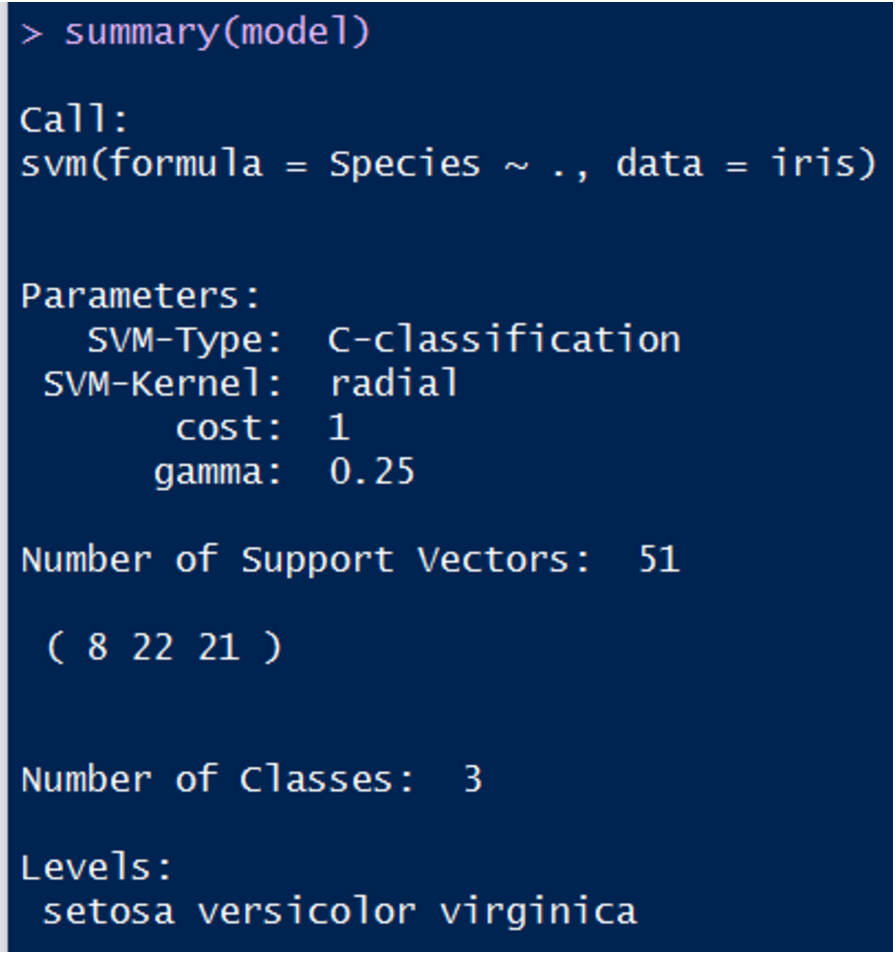
其中,SVM类型是C-classification,核函数是高斯核,cost是误分点容忍度参数,gamma是核函数参数。他们的具体含义请参考函数手册。
4. 利用该模型进行预测

5. 查看预测效果:
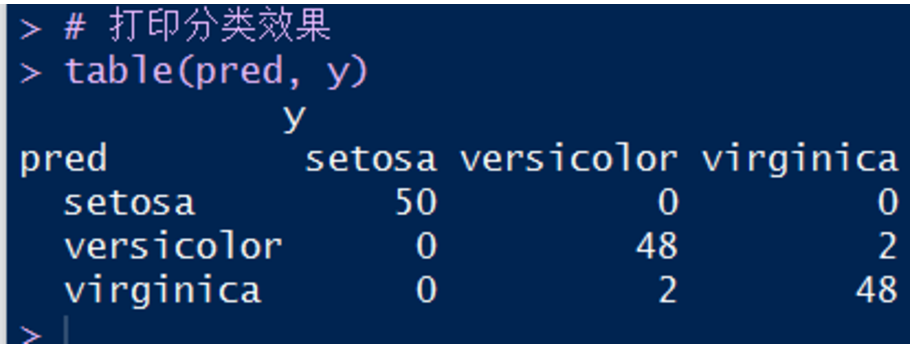
可见,有两个类型似乎混淆了。那怎么办?还有,如果变量多,我如何观察出哪几个变量纠缠不清呢?下面先来解决这个问题。
6. 使用MDS技术查看各变量分类情况
MDS技术可以根据所有样本之间的距离,根据各个变量之间距离不变的设定,将维度降低到两维。一般来说,它是用来分析整体分类的一个态势的:
1 plot(cmdscale(dist(iris[,-5])), col = c("blue", "green", "orange")[as.integer(iris[,5])], pch = c("o", "+")[1:150 %in% model$index+1]) 2 legend(2, -0.7, c("setosa", "versicolor", "virginica"), col = c("blue", "green", "orange"), lty = 1)
显示效果如下:
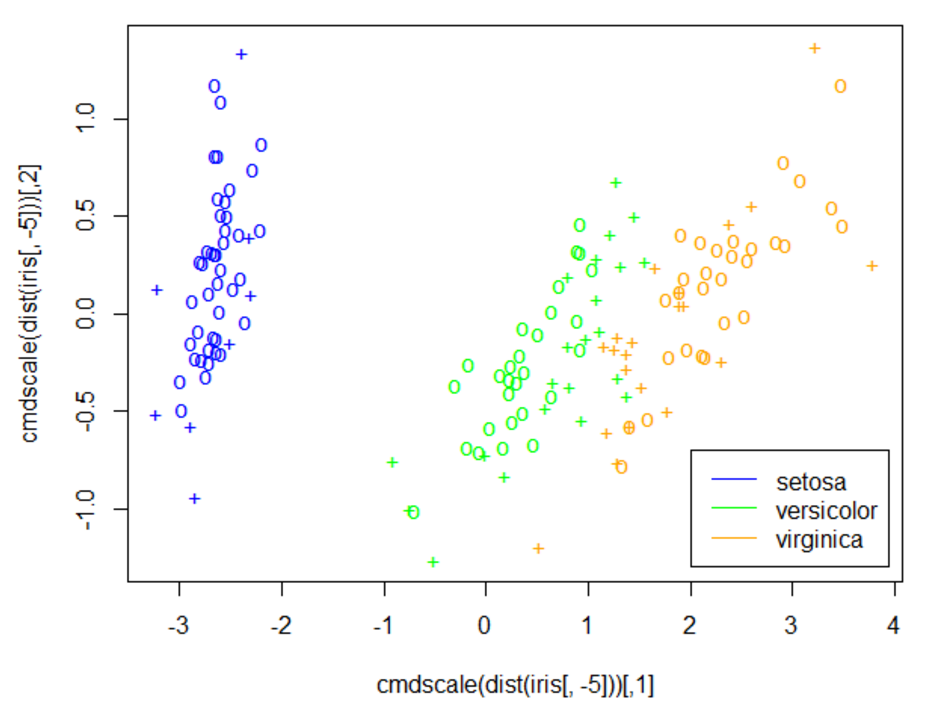
显然,后两个分类有点混淆。
7. 调整各样本权重系数:
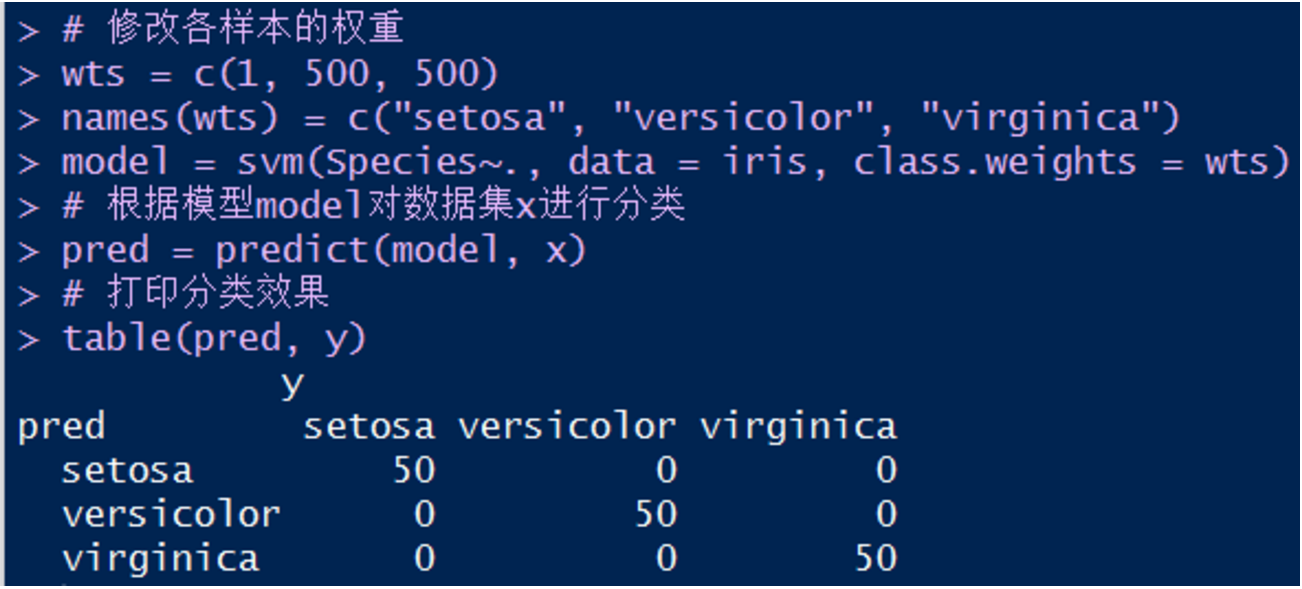
由上图可知,这样的模型产生了更好的分类效果。
小结
1. 本例中的场景比较简单,故未做复杂的参数调整。在实际项目中往往需要对方方面面都进行调整。
2. 虽然SVM在做了标准化后效果更好,但是不用手动标准化。因为SVM函数会自动进行标准化。
3. 对于维度比较少的情况,直接用线性核就好了。
4. SVM是综合指标最好的分类器,但是有它的局限之处,那就是容易过拟合。因此降维工作一定要做好。