K均值(K-Means)算法是一种无监督的聚类学习算法,他尝试找到样本数据的自然类别,分类是K由用户自己定义,K均值在不需要任何其他先验知识的情况下,依据算法的迭代规则,把样本划分为K类。K均值是最常用的聚类技术之一,通过不断迭代和移动质心来完成分类,与均值漂移算法的原理很相似。
K均值算法的实现过程:
- 1. 对于一组未知分类的数据集合,指定其分类数K;
- 2. 随机分配K个类别的中心点位置,分配的原则是各个类别的中心点距离彼此越远越好。
- 3.将数据集中的每一个点进行类别划分,划分的距离N个初始的类别中心点中哪一个的距离最近,就划入哪一类;
- 4.根据上一步中初步划分的N个类别,分别计算当前每一类的样品中心,并移动初始中心点到当前集合所在的中心。
- 5.去除数据集合中每个点的归类属性,依据上边产生的中心点,转到第3步,迭代执行,直到中心点收敛。
K均值的核心就是不断移动类别划分的中心点,直到该点稳定下来或者达到所设置的最大迭代次数,这时当前中心点所划分的类别就是最终的K均值对样本数据的聚类。
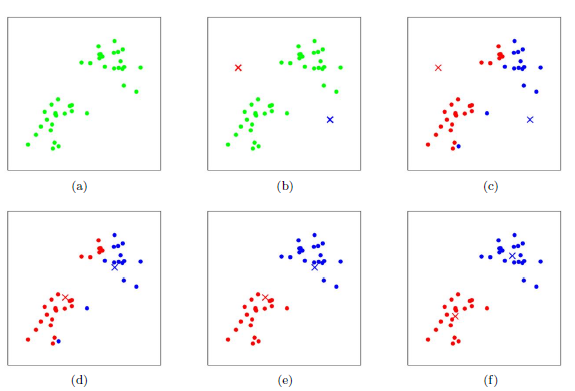
下图是对K-Means迭代过程的简单演示。假设有n 个数据样本需要进行分类,这里k取值 为2:
(a)初始数据集合
(b)随机选取两个点作为初始聚类中心
(c)计算每个点到聚类中心的距离,并聚类到离该点最近的聚类中去
(d)计算每个聚类中所有点的坐标平均值,并将这个平均值 作为新的聚类中心
(e)重复(c),计算每个点到聚类中心的距离,并聚类到离该点最近的聚类中去
(f) 重复(d),计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心,直到满足迭代条件。
虽然K-Means算法原理简单,也有自身的缺陷:
- 1.K值的选择需要用户指定,实际中K值 的估计很难做到准确,并且不同的K值得到的结果可能差别很大。
- 2.初始的聚类中心点的设定对结果影响较大。不同的初始聚类中心可能导致完全不同的聚类结果,并且不能保证K-Means算法收敛于全局最优解,极端情况下有可能达到局部收敛。
- 3.时间复杂度高0(nkt),其中n是对象总数,k是簇数,t是迭代次数。数据库较大的时候,收敛会比较慢。
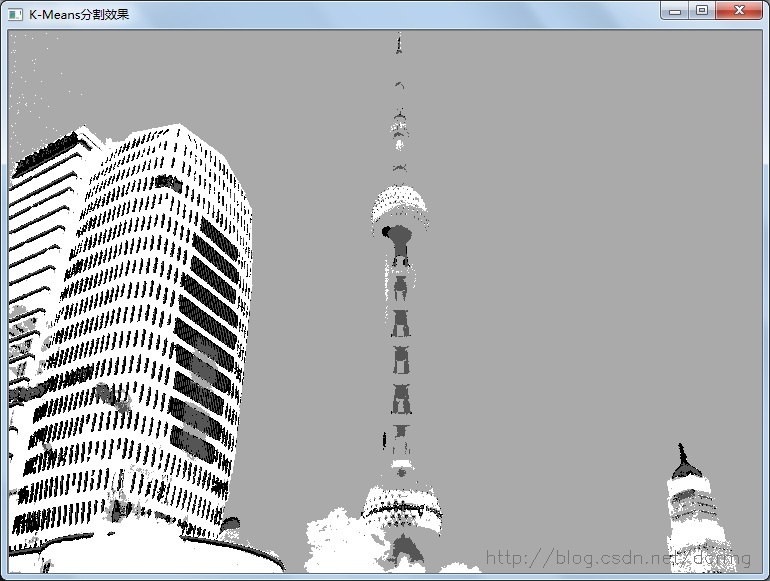
以下是用K-Means算法对一幅图像进行分割的代码实现:
#include <iostream>
#include <opencv2/core/core.hpp>
#include <imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/ml/ml.hpp>
using namespace cv;
using namespace std;
int main(int argc, char* argv[])
{
Mat img =imread("Sky.jpg");
namedWindow("Source Image",0);
imshow("Source Image", img);
//生成一维采样点,包括所有图像像素点,注意采样点格式为32bit浮点数。
Mat samples(img.cols*img.rows, 1, CV_32FC3);
//标记矩阵,32位整形
Mat labels(img.cols*img.rows, 1, CV_32SC1);
uchar* p;
int i, j, k=0;
for(i=0; i < img.rows; i++)
{
p = img.ptr<uchar>(i);
for(j=0; j< img.cols; j++)
{
samples.at<Vec3f>(k,0)[0] = float(p[j*3]);
samples.at<Vec3f>(k,0)[1] = float(p[j*3+1]);
samples.at<Vec3f>(k,0)[2] = float(p[j*3+2]);
k++;
}
}
int clusterCount = 4;
Mat centers(clusterCount, 1, samples.type());
kmeans(samples, clusterCount, labels,
TermCriteria( CV_TERMCRIT_EPS+CV_TERMCRIT_ITER, 10, 1.0),
3, KMEANS_PP_CENTERS, centers);
//我们已知有3个聚类,用不同的灰度层表示。
Mat img1(img.rows, img.cols, CV_8UC1);
float step=255/(clusterCount - 1);
k=0;
for(i=0; i < img1.rows; i++)
{
p = img1.ptr<uchar>(i);
for(j=0; j< img1.cols; j++)
{
int tt = labels.at<int>(k, 0);
k++;
p[j] = 255 - tt*step;
}
}
namedWindow("K-Means分割效果",0);
imshow("K-Means分割效果", img1);
waitKey();
return 0;
}原始图像:
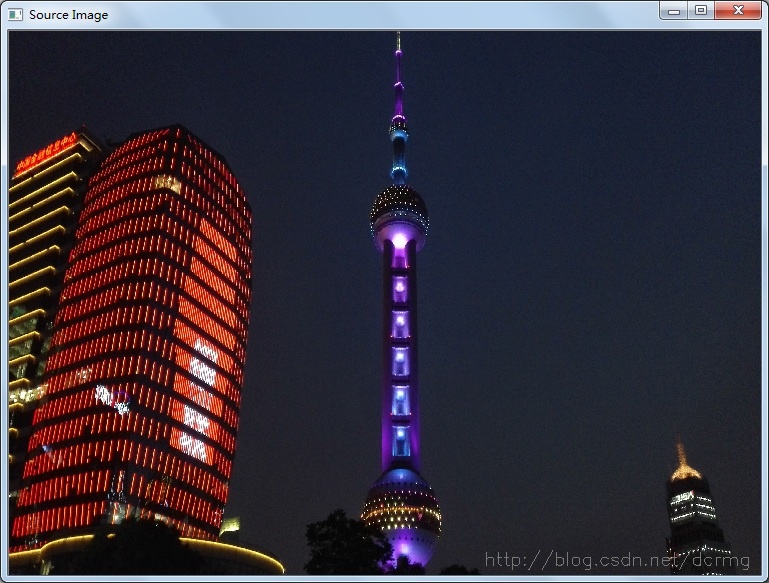
由于原图像素大小是4160X2336,计算时候也没有进行压缩,所以K-Means的迭代消耗时间也是很可观的,在我的机器上整个耗时约60S。
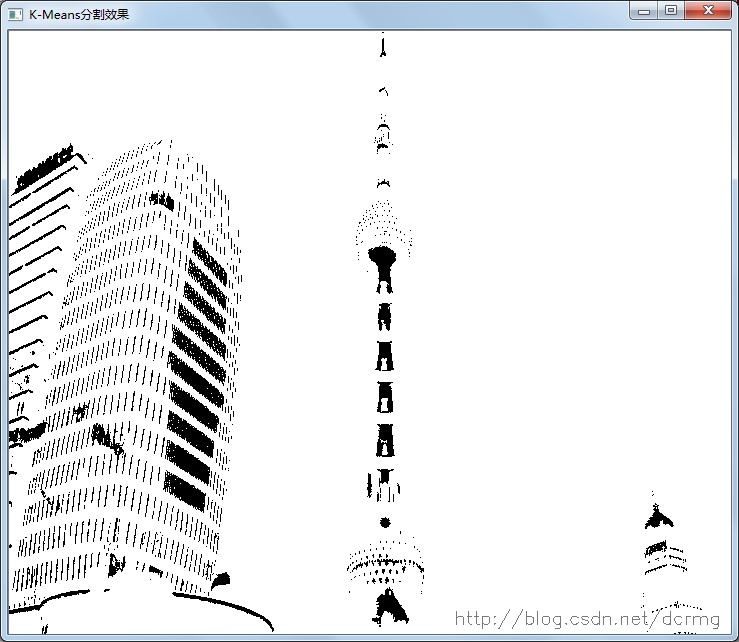
对图像进行分割,采用K=2效果:
K=3效果:

K=4效果: