Bet Class
- class
strats.Bet(inp)[source] -
Here is an example of the expected string input on instantiation of the class. It is expecting a string using the POST method in a cgi script receiving a textarea input from an HTML form.
As one can see, the expected text that looks like Python code. This means that these variables can be immediately “compiled” into the code for the class upon instantiation. This is an example of a string for betting on the trifecta that is passed to the class instantiation code,
__init__().self.bet_type = "Trifecta" self.nraces = 1 self.horse_ids.append([1,2,4,5,6,8,9]) self.user_odds.append([2.0,4.2,4.2,5.5,5.9,9.4,11.0]) self.tab_odds.append([3.9,7.2,4.2,5.5,5.9,9.4,11.0]) self.jockeys.append([1,2,3,4,5,6,7]) self.trainers.append([1,2,3,4,5,6,7]) self.standouts_1.append([1,2]) self.standouts_2.append([1,2,4,5]) self.standouts_3.append([]) self.value = True self.scale_var = 100 user_div_range = (0,750) tab_div_range = (750,5000)Note
- I think there needs to be some variables to describe what to do with the jockey and trainer info?
- I don’t understand
max_tab_market_oddswell enough to code it. - Do we need the client’s ID?
- Do we need the Race ID?
- I think we will need to establish an order in which the rules are applied.
- Do we need to specify the stake for flat staking?
- Is there some kind of incosistency between enforcing total outlay as a restriction and the staking rules including round the rounding rules?
__init__(inp)[source]-
Parameters: inp (string) – user input as string probably from digesting a cgi transmission of a textarea html form element Returns: None
__module__= 'strats'
bet_type= None-
One of Quinella, Exacta, Trifecta, Pick 4, Pick 6, Quaddy, Superfecta
error_message(msg)[source]-
This routine sends a error_message to the user. (usually because there is something wrong with the input.)
Return type: None Parameters: msg – error_message string Returns: nil
fifth= []-
fifth place standouts (after [] substitution)
find_common_combinations_and_sort(tabres, userres)[source]-
Due to restrictions on win price lines and trifecta probabilities is is possible for the tab and user lists of probabilites mto not have the same combinations. This routine finds the common combinations and applies the overlay if specified.
Parameters: - tabres – list of tuples of (combinations,tab probabilities)
- userres –
Returns: list of tuples containing (combination, tab probability, user probability)
first= []-
first place standouts (after [] substitution)
flat_stakes= True-
Flat stakes flag, if True, must define stake
fourth= []-
fourth place standouts (after [] substitution)
get_multi_tab_restricted_ids(p, w, n)[source]-
This routine restricts a price line according to
Return type: list of ints
Parameters: - p – user or tab probability from win price line
- w – one of [tabodds1, tabodds2, ..., userodds1, userodds2,...] odds limits for price line and position
- n – for nth race
Returns: tab ids consistent with odds restrictions
get_tab_restricted_ids(p, w)[source]-
This routine restricts a price line according to
Parameters: - p – user or tab probability from win price line
- w – one of [tabodds1, tabodds2, ..., userodds1, userodds2,...] odds limits for price line and position
Returns: tab ids consistent with odds restrictions
handle_both_price_lines(tabres, userres)[source]-
Once the combination probabilities are calculated (including standouts and odds restrctions), this routine applies all of the other rules for betting if both tab and user price lines are provided. The logic is
- convert (id,prob) tuples into dictionaries
- find common TAB ids (odds restrictions enforce this)
- restrict combinations for overlay if required
- restrict combination by % number, % value, or total stake
- calculate staking for each combination according to flat_staking flag and rounding option
- print results
Parameters: - tabres – list of tuples (combinations, tab probabilities)
- userres – list of tuples (combinations, user probabilities)
Returns: None
Return type:
handle_exacta()[source]-
This routine handles the details of impmenting the rules when betting on the exacta.
Return type: None Returns: number of bets, outlay, list of combinations
handle_pick4()[source]-
This routine handles the details of impmenting the rules when betting on the pick 4 pools.
Return type: None Returns: number of bets, outlay, list of combinations
handle_pick6()[source]-
This routine handles the details of impmenting the rules when betting on the pick 6 pools.
Return type: None Returns: number of bets, outlay, list of combinations
handle_quaddie()[source]-
This routine handles the details of impmenting the rules when betting on the pick 4 pools.
Return type: None Returns: number of bets, outlay, list of combinations
handle_quinella()[source]-
This routine handles the details of impmenting the rules when betting on the exacta.
Return type: None Returns: number of bets, outlay, list of combinations
handle_single_price_line(singleres)[source]-
Once the combination probabilities are calculated (including standouts and odds restrctions), this routine applies all of the other rules for betting if both tab and user price lines are provided. The logic is
- restrict combination by % number, % value, or total stake
- calculate staking for each combination according to flat_staking flag and rounding option
- print results
Parameters: singleres – list of tuples (combinations, tab or user probabilities) Returns: None Return type: None
handle_superfecta()[source]-
This routine handles the details of impmenting the rules when betting on tsuperfecta.
Return type: None Returns: number of bets, outlay, list of combinations
handle_trifecta()[source]-
This routine handles the details of impmenting the rules when betting on the trifecta.
Return type: None Returns: number of bets, outlay, list of combinations
horse_ids= []-
list of lists of TAB ids for horses (one list for each race)
jockey_list= []-
list of lists of jockeys (one for each race) This parameter is only for multiple race bets.
max_tab_market_odds= (0, 0)-
I don’t know how to define this. Currently unimplemented
multi_race_preprocess(nraces)[source]-
This routine handles the preprocessing for multiple race betting pools:
nracesneeds to be 1- at least one of user odds or TAB odds must be provided
- ensure that odds are only for one race
- list of horse TAB ids must be provided and be of same length as odds provided
- check to make sure jockey and trainer info not provided
Process input in the following order
- remove scratchings, taking care to delete runner info from end of the appropriate lists
- scale TAB and/or user odds
- process standouts
Parameters: nraces (int) – number of races for pool Returns: Flag for tab divs, flag for user divs, tab prob list, user prob list
multi_race_scale_odds(ntabodds, nuserodds)[source]-
This routine scales the odds and calculates the relevant probability of the user and/or tab win price line.
Parameters: - ntabodds – 1 if have tab odds, 0 otherwise
- nuserodds – 1 if have user odds, 0 otherwise
Returns: tab prob list, user prob list
multi_race_scratchings(ntabodds, nuserodds)[source]-
Parameters: - ntabodds – 1 if tab odds present, 0 otherwise
- nuserodds – 1 if user odds present, 0 otherwise
Returns: None
multi_race_validation(nraces)[source]-
This routine checks for a number of possible input errors for a single race pool.
Returns:
nraces= 0-
number of races for which data is input
outlay_amount= 10000000.0-
cap on outlay be in order of probability
overlay= False-
True if value betting; else False
overlay_scale= 1.0-
If value betting, bet if (user_div * overlay_scale) <= tab_div
percent_by_number= 0-
Top percent of bets by number accepted after all other conditions applied if 100, accept all, if <= 0 dont’t calculate
percent_by_value= 0-
Top percent of bets by value accepted after all other conditions applied if 100, accept all, , if <= 0, don’t calculate
prob_exacta(prob, s1, s2, sort=False)[source]-
This routine calculates the normalized exacta probabilites given an input list of horse ids and normalized win probabilities.
If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (first) and jj (second) as the winning combination is given by

-
Return type: Parameters: - prob – list of tuples of form (id,win probability)
- s1 – list of allowed first place ids defined by odds range
- s2 – list of allowed second place ids defined by odds range
- sort – Boolean if True, result is sorted, highest probability first
Returns: list of tuples of form ((id1,id2),exacta_probability)
So if we input prob as:
(1, 0.15557814847495188) (2, 0.20438859122263553) (3, 0.3708534602327072) (4, 0.19948464099114765) (5, 0.034061786039927267) (6, 0.021204203862783776) (7, 0.0031196067348740163) (8, 0.01130956244097265)The first few exacta probabilities (if unsorted) would be:
(1, 2) 0.0476639105054 (1, 3) 0.117045542403 (1, 4) 0.0461010957068 (1, 5) 0.00569989602184 (1, 6) 0.00345321559886 (1, 7) 0.000488654491335 (1, 8) 0.0018032135443
If sorted, the first few exacta probabilities would be:
(3, 2) 0.12047784021 (3, 4) 0.11758718311 (2, 3) 0.0952703989043 (4, 3) 0.0924149281363 (3, 1) 0.0917062894757 (1, 3) 0.0683268612653 (2, 4) 0.0512466064374
prob_pick4(prob, s1, s2, s3, s4, sort=False)[source]-
This routine calculates the normalized first four probabilites given an input list of horse ids and normalized win probabilities.
If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (first), jj (second), kk (third), and ll (fourth)as the winning combination is given by

-
Return type: Parameters: - prob – list of tuples of form (id,win probability)
- s1 – list of allowed first place ids defined by odds range
- s2 – list of allowed second place ids defined by odds range
- s3 – list of allowed third place ids defined by odds range
- s4 – list of allowed fourth place ids defined by odds range
- sort – Boolean if True, result is sorted, highest probability first
Returns: list of tuples of form ((id1,id2,id3,id4),pick 4 probability)
So if we input prob as:
(1, 0.15557814847495188) (2, 0.20438859122263553) (3, 0.3708534602327072) (4, 0.19948464099114765) (5, 0.034061786039927267) (6, 0.021204203862783776) (7, 0.0031196067348740163) (8, 0.01130956244097265)The first few pick 4 probabilities (if unsorted) would be:
(1, 2, 3, 4) 0.0161700951381 (1, 2, 3, 5) 0.00276102620283 (1, 2, 3, 6) 0.00171879896159 (1, 2, 3, 7) 0.000252873291125 (1, 2, 3, 8) 0.000916745769159 (1, 2, 4, 3) 0.00988009673754 (1, 2, 4, 5) 0.000907457465589 (1, 2, 4, 6) 0.000564912041741 (1, 2, 4, 7) 8.3111038803e-05 (1, 2, 4, 8) 0.000301303838195
If sorted, the first few pick 4 probabilities would be:
(1, 2, 3, 4) 0.0161700951381 (1, 2, 3, 5) 0.00276102620283 (1, 2, 3, 6) 0.00171879896159 (1, 2, 3, 7) 0.000252873291125 (1, 2, 3, 8) 0.000916745769159 (1, 2, 4, 3) 0.00988009673754 (1, 2, 4, 5) 0.000907457465589 (1, 2, 4, 6) 0.000564912041741 (1, 2, 4, 7) 8.3111038803e-05 (1, 2, 4, 8) 0.000301303838195
prob_pick6(prob, s1, s2, s3, s4, s5, s6, sort=False)[source]-
This routine calculates the normalized first six probabilites given an input list of horse ids and normalized win probabilities.
If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (first), jj (second), kk (third), :param s1: ll (fourth), mm (fifth), and nn (sixth) as the winning combination is given by
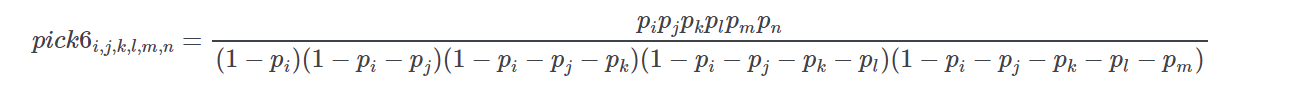
-
Return type: Parameters: - prob – list of tuples of form (id,win probability)
- s1 – list of allowed first place ids defined by odds range
- s2 – list of allowed second place ids defined by odds range
- s3 – list of allowed third place ids defined by odds range
- s4 – list of allowed fourth place ids defined by odds range
- s5 – list of allowed fifth place ids defined by odds range
- s6 – list of allowed sixth place ids defined by odds range
- sort – Boolean if True, result is sorted, highest probability first
Returns: list of tuples of form ((id1,id2,id3,id4,id5,id6),pick 6 probability)
So if we input prob as:
(1, 0.15557814847495188) (2, 0.20438859122263553) (3, 0.3708534602327072) (4, 0.19948464099114765) (5, 0.034061786039927267) (6, 0.021204203862783776) (7, 0.0031196067348740163) (8, 0.01130956244097265)The first few pick 6 probabilities (if unsorted) would be:
(1, 2, 3, 4, 5, 6) 0.00470264737409 (1, 2, 3, 4, 5, 7) 0.000691863298187 (1, 2, 3, 4, 5, 8) 0.00250822357959 (1, 2, 3, 4, 6, 5) 0.00345572050302 (1, 2, 3, 4, 6, 7) 0.000316498052757 (1, 2, 3, 4, 6, 8) 0.00114740568101 (1, 2, 3, 4, 7, 5) 0.000370307449629 (1, 2, 3, 4, 7, 6) 0.000230524454726
If sorted, the first few pick 6 probabilities would be:
(3, 2, 4, 1, 5, 6) 0.0113643296974 (3, 4, 2, 1, 5, 6) 0.0112346228107 (3, 2, 1, 4, 5, 6) 0.00951066959114 (3, 4, 1, 2, 5, 6) 0.0092338952488 (2, 3, 4, 1, 5, 6) 0.00898658393663 (4, 3, 2, 1, 5, 6) 0.00882959207139 (3, 1, 2, 4, 5, 6) 0.00853040992409 (3, 1, 4, 2, 5, 6) 0.00837778246743
Timings of routine with n sized fields n Unsorted (sec) Sorted (sec) 6 0.002 0.004 8 0.037 0.128 10 0.247 1.12 12 1.10 5.60 14 3.95 23.8 16 13.1 97.2 18 62.3 20 Memory
prob_quaddie(ids, prob, s1, s2, s3, s4, sort=False)[source]-
This routine calculates the quaddie probabilites given an input list of horse ids and normalized win probabilities for each of the four races
If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (in the first race), jj (in the second race), kk (in the third race), and ll (in the fourth race)as the winning combination is given by
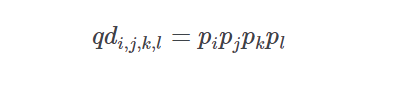
-
Parameters: - sort – if True sor by increasing probability
- ids – list of lists of TAB horse ids
- prob – list of lists of tuples of win probability) for each race
- s1 – list of horse ids to be considered for win in first race
- s2 – list of horse ids to be considered for win in second race
- s3 – list of horse ids to be considered for win in third race
- s4 – list of horse ids to be considered for win in fourth race
Return type: Returns: list of tuples of form ((id1,id2,id3,id4),quaddie probability)
So if we input the four race probabilities as:
1 0.15558 1 0.86564 1 0.04397 1 0.76204 2 0.20439 2 0.02050 2 0.04988 2 0.10846 3 0.37085 3 0.02690 3 0.85491 3 0.08160 4 0.19948 4 0.06478 4 0.04690 4 0.01898 5 0.03406 5 0.01119 5 0.00072 5 0.01083 6 0.02120 6 0.00605 6 0.00096 6 0.01692 7 0.00312 7 0.00172 7 0.00267 7 0.00117 8 0.00788 8 0.00068 8 0.00000 9 0.00180 9 0.00230 9 0.00001 10 0.00068 10 0.00024 10 0.00000 11 0.00009 11 0.00000 12 0.00087
The first few quaddie probabilities (if unsorted) would be:
(1, 1, 1, 1) 0.00451204255393 (1, 1, 1, 2) 0.000642180234069 (1, 1, 1, 3) 0.000483129743111 (1, 1, 1, 4) 0.000112363248935 (1, 1, 1, 5) 6.41234861406e-05 (1, 1, 1, 6) 0.000100176763996 (1, 1, 1, 7) 6.93229347721e-06 (1, 1, 1, 8) 1.50345086741e-08 (1, 1, 1, 9) 5.73763223463e-08
If sorted, the first few quaddie probabilities would be:
(3, 1, 3, 1) 0.2091383481 (2, 1, 3, 1) 0.115262487539 (4, 1, 3, 1) 0.112496963793 (1, 1, 3, 1) 0.0877364254662 (3, 1, 3, 2) 0.0297657904886 (3, 1, 3, 3) 0.0223936177872 (5, 1, 3, 1) 0.0192087345262 (2, 1, 3, 2) 0.0164048300393 (4, 1, 3, 2) 0.0160112245568 (3, 4, 3, 1) 0.0156519771072
Timings of routine with n sized fields for 4 races n Unsorted (sec) Sorted (sec) 2 0 0 4 0 .003 6 .002 .007 8 .003 .018 10 .006 .049 12 .012 .109 14 .02 .215 16 .037 .40 18 .059 .648 20 .288 2.62
prob_quinella(prob, s1, s2, sort=False)[source]-
This routine calculates the normalized quinella probabilites given an input list of horse ids and normalized win probabilities.
If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii and jj as the winning combination is given by
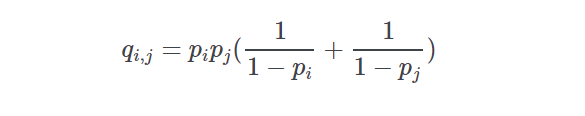
-
Return type: Parameters: - prob – list of tuples of form (id,win probability)
- s1 – list of allowed first place ids defined by odds range
- s2 – list of allowed second place ids defined by odds range
- sort – Boolean if True, result is sorted, highest probability first
Returns: list of tuples of form ((id1,id2),quinella_probability)
So if we input prob as:
(1, 0.15557814847495188) (2, 0.20438859122263553) (3, 0.3708534602327072) (4, 0.19948464099114765) (5, 0.034061786039927267) (6, 0.021204203862783776) (7, 0.0031196067348740163) (8, 0.01130956244097265)The first few quinella probabilities (if unsorted) would be:
(1, 0.15557814847495188) (2, 0.20438859122263553) (3, 0.3708534602327072) (4, 0.19948464099114765) (5, 0.034061786039927267) (6, 0.021204203862783776) (7, 0.0031196067348740163) (8, 0.01130956244097265)If sorted, the first few quinella probabilities would be:
(2, 3) 0.215748239115 (3, 4) 0.210002111247 (1, 3) 0.160033150741 (2, 4) 0.102179276603 (1, 2) 0.0776242539698 (1, 4) 0.0755228299148 (3, 5) 0.0331552537388 (3, 6) 0.0205329272655 (2, 5) 0.0159576376265
prob_superfecta(ids, prob, s1, s2, s3, s4, s5, s6, sort=False)[source]-
This routine calculates the quaddie probabilites given an input list of horse ids and normalized win probabilities for each of the four races
If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (in the first race), jj (in the second race), kk (in the third race), and ll (in the fourth race)as the winning combination is given by
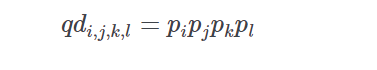
-
Parameters: - sort – if True sor by increasing probability
- ids – list of lists of TAB horse ids
- prob – list of lists of tuples of win probability) for each race
- s1 – list of horse ids to be considered for win in first race
- s2 – list of horse ids to be considered for win in second race
- s3 – list of horse ids to be considered for win in third race
- s4 – list of horse ids to be considered for win in fourth race
- s5 – list of horse ids to be considered for win in fifth race
- s6 – list of horse ids to be considered for win in sixth race
Return type: Returns: list of tuples of form ((id1,id2,id3,id4,id5,id6),quaddie probability)
prob_trifecta(prob, s1, s2, s3, sort=False)[source]-
This routine calculates the trifecta probabilites given an input list of horse ids and normalized win probabilities.
If pp is the vector of win probabilities derived from a price line then the probability of runner ii (first), jj (second), and kk (third) as the winning combination is given by
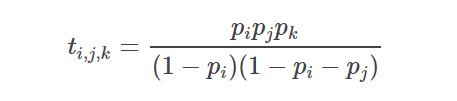
-
Return type: Parameters: - prob – list of tuples of form (id,win probability)
- s1 – list of allowed first place ids defined by odds range
- s2 – list of allowed second place ids defined by odds range
- s3 – list of allowed third place ids defined by odds range
- sort – Boolean if True, result is sorted, highest probability first
Returns: list of tuples of form ((id1,id2,id3),trifecta_probability)
So if we input prob as:
(1, 0.15557814847495188) (2, 0.20438859122263553) (3, 0.3708534602327072) (4, 0.19948464099114765) (5, 0.034061786039927267) (6, 0.021204203862783776) (7, 0.0031196067348740163) (8, 0.01130956244097265)The first few trifecta probabilities (if unsorted) would be:
(1, 2, 3) 0.0218195393628 (1, 2, 4) 0.0117368811219 (1, 2, 5) 0.0020040597189 (1, 2, 6) 0.00124757083445 (1, 2, 7) 0.000183545225398 (1, 2, 8) 0.000665409573642 (1, 3, 2) 0.0294893645215 (1, 3, 4) 0.0287818182974
If sorted, the first few trifecta probabilities would be:
(3, 2, 4) 0.0565815867228 (3, 4, 2) 0.0559357922362 (2, 3, 4) 0.0447430857683 (3, 2, 1) 0.0441280013156 (4, 3, 2) 0.0439614427612 (3, 4, 1) 0.0425776553257 (3, 1, 2) 0.0395797516406 (3, 1, 4) 0.0386301040548 (2, 3, 1) 0.0348951498537
process_multi_race_standouts()[source]-
Define single race standouts for first, second, third, fourth, fifth, sixth
Returns: None
process_single_race_standouts()[source]-
Define single race standouts for first, second, third, fourth, fifth, sixth
Returns: None
rounding= 'Round Up'-
type of rounding, one of [“Exact”,”Round Up”,”Round_Down”,”Nearest”]
roundit(y)[source]-
Parameters: y – stake amount Returns: stake amount rounded according to rounding parameter
scale_tab= 0-
scale TAB market by % (0 is normalized, -1 unscaled, otherwise < 100)
scale_user= 0-
scale user market by % (0 is normalized, -1 unscaled, otherwise < 100)
second= []-
second place standouts (after [] substitution)
single_race_preprocess()[source]-
This routine handles the preprocessing for single race betting pools:
nracesneeds to be 1- at least one of user odds or TAB odds must be provided
- ensure that odds are only for one race
- list of horse TAB ids must be provided and be of same length as odds provided
- check to make sure jockey and trainer info not provided
Process input in the following order
- remove scratchings, taking care to delete runner info from end of the appropriate lists
- scale TAB and/or user odds
- process standouts
Returns: Flag for tab divs, flag for user divs, tab prob list, user prob list
single_race_scale_odds(ntabodds, nuserodds)[source]-
This routine scales the odds and calculates the relevant probability of the user and/or tab win price line.
Parameters: - ntabodds – 1 if have tab odds, 0 otherwise
- nuserodds – 1 if have user odds, 0 otherwise
Returns: tab prob list, user prob list
single_race_scratchings(ntabodds, nuserodds)[source]-
Parameters: - ntabodds – 1 if tab odds present, 0 otherwise
- nuserodds – 1 if user odds present, 0 otherwise
Returns: None
single_race_validation()[source]-
This routine checks for a number of possible input errors for a single race pool.
Returns:
sixth= []-
sixth place standouts (after [] substitution)
stake= 0.5-
Amount to stake on each combination if flat_stakes is True
standouts_1= []-
list of standouts for first place. Generally speaking, if standouts are given for any place in one race pools or any leg for multi race pools, the rest must be specified as well. If one wants to bet the field then the entry shoud be the empty list.
example for a single race, [1,3,4]
Alternatively for multi-race bets, it standouts for first in the first race
standouts_2= []-
list of standouts for second place. Alternatively for multi-race bets, it standouts for first in the second race
standouts_3= []-
list of standouts for third place. Alternatively for multi-race bets, it standouts for first in the third race
standouts_4= []-
list of standouts for fourth place. Alternatively for multi-race bets, it standouts for first in the fourth race
standouts_5= []-
list of standouts for fifth place. Alternatively for multi-race bets, it standouts for first in the fifth race
standouts_6= []-
list of standouts for sixth place. Alternatively for multi-race bets, it standouts for first in the sixth race
tab_div_range= False-
Dividend range for TAB price line; eg, (100,1000), or False for no check
tab_odds= []-
list of lists of TAB odds (one list for each race)
tabodds1= []-
1st favourite restricted to (min,max) tab odds, empty list accept all odds
tabodds2= []-
2nd favourite restricted to (min,max) tab odds, empty list accept all odds
tabodds3= []-
3rd favourite restricted to (min,max) tab odds, empty list accept all odds
tabodds4= []-
4th favourite restricted to (min,max) tab odds, empty list accept all odds
tabodds5= []-
5th favourite restricted to (min,max) tab odds, empty list accept all odds
tabodds6= []-
6rd favourite restricted to (min,max) tab odds, empty list accept all odds
takeout= 100-
Takeout amount
takeout_priceline= 'tab'-
price line use for takeout cqalculation, must be one of [“tab”,”user”]
third= []-
third place standouts (after [] substitution)
trainer_list= []-
list of lists of trainer lists (one for each race) This parameter is only for multiple race bets.
user_div_range= False-
Dividend range for user price line; eg, (100,1000), or False for no check
user_odds= []-
list of lists of user odds (one list for each race)
userodds1= []-
1st favourite restricted to (min,max) user odds, empty list accept all odds
userodds2= []-
2nd favourite restricted to (min,max) user odds, empty list accept all odds
userodds3= []-
3rd favourite restricted to (min,max) user odds, empty list accept all odds
userodds4= []-
4th favourite restricted to (min,max) user odds, empty list accept all odds
userodds5= []-
5th favourite restricted to (min,max) user odds, empty list accept all odds
userodds6= []-
6rd favourite restricted to (min,max) user odds, empty list accept all odds
-
-
-
-
-
-
-