图的数据结构为邻接链表adjacency list。
listVertex是一个储存Vertex* 顶点类指针的vector类型的STL;在Vertex类中有一个类成员nextEdgeNode,他是储存pair<int,int>类型的vector容器;数对pair的first表示边指向的顶点序号,second表示边的序号。
四个函数都只有一个参数,在声明时提供了默认的参数值-1;参数表示起始顶点的编号
先放一个测试用的图、有向图的邻接链表、无向图的邻接链表。
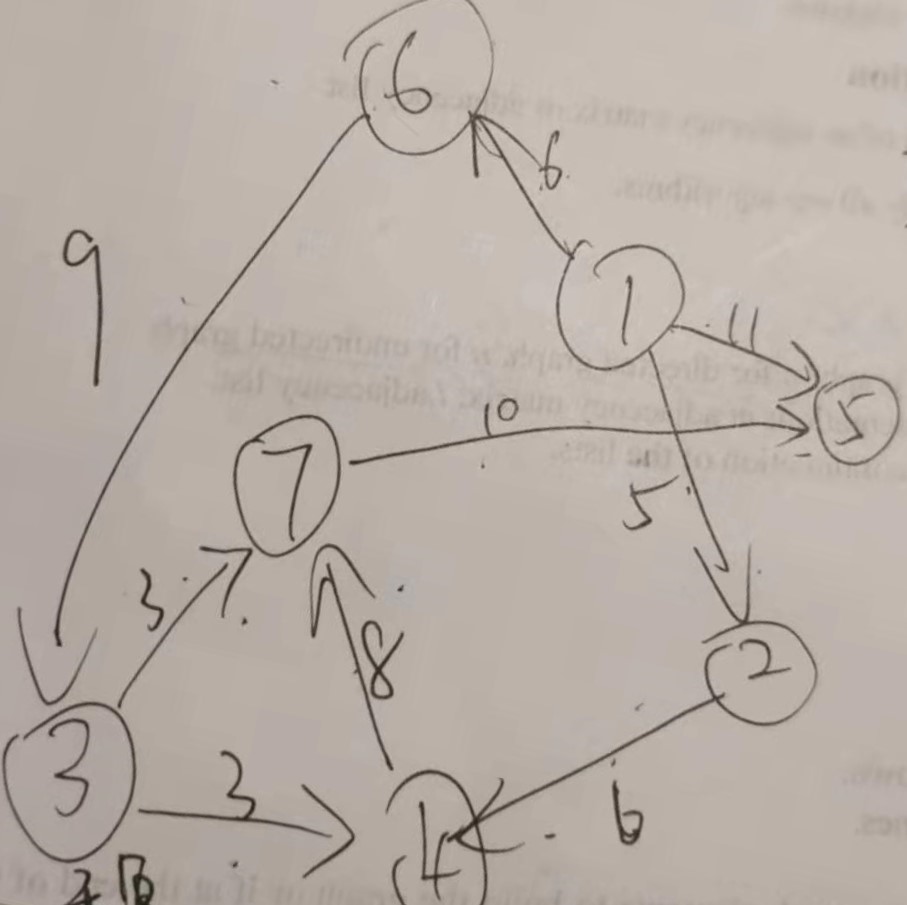


以下是有向图的BFS
1 void Graph::BFSListO(int startFrom) { 2 /*the principle is to firstly choose a random vertex, if it has 0 out degree, then choose the first 3 unvisited vertex in the list; moreover,if one way is exhausted to continue,also push the first univisited vertex 4 in the list to the queue*/ 5 cout << "BFS of oriented Adjacey List:" << endl; 6 srand((unsigned int)time(NULL)); 7 int sze = listVertex.size(); 8 int rdm = rand() % sze ;//[0,sze) 9 while (listVertex[rdm]->nextEdgeNode.empty()) { 10 rdm = rand() % sze;//randomly choose a vertex whose out degree is not 0 11 } 12 queue<Vertex*> myQueue; 13 if(startFrom==-1)//default treatment is random choose 14 myQueue.push(listVertex[rdm]); 15 else {//designated choose 16 myQueue.push(listVertex[startFrom-1]); 17 } 18 while (!myQueue.empty()) {// travel through until there is nothing in the queue 19 Vertex* V = myQueue.front(); 20 if (V->color == 0) { 21 V->color = 1; //O black(unvisited) & 1 white(visited)//V visited white 1 22 cout << "Vertex visited:" << V->id +1<< endl; 23 } 24 if (!V->nextEdgeNode.empty()) {//if the out degree is not zero 25 for (auto it = V->nextEdgeNode.begin(); it != V->nextEdgeNode.end(); it++) {//travel through all outgoing vertices 26 if(listVertex[(*it).first - 1]->color==0) 27 myQueue.push(listVertex[(*it).first-1]);//push into queue for next round travel 28 } 29 } 30 else {//if the first chosed vertex has zero out degree, then add the first unvisited vertex from list 31 for (auto it = listVertex.begin(); it != listVertex.end(); it++) { 32 if ((*it)->color == 0) {//if unvisited 33 myQueue.push(*it); 34 break;/*ATTENTION without this line the algo will be wrong ! 35 because more than one unvisited vertex has been added to queue, 36 which causes a sequential fault*/ 37 } 38 } 39 } 40 myQueue.pop(); 41 42 } 43 }
其实有向图比无向图复杂得多。19行以前都在初始化,把第一个顶点放入队列。这里使用FIFO队列进行辅助。每一次循环,总是先访问队头顶点;然后从这个顶点开始遍历(不是访问)他的所有子顶点,将他们加入队尾;最后把这个元素弹出队列。
这里需要注意有向图的特殊之处:有的顶点可能出度为零,因此需要加入26和32行的判断语句,如果被访问了的这个顶点没有子顶点,则按顺序选择一个未被访问过的顶点,加入队尾(注意只能选择一个哦,不要忘记break)
输出示例:

以下是无向图的BFS
1 void Graph::BFSListN(int startFrom) { 2 /*the principle is to firstly choose a random vertex, if it has 0 out degree, then choose the first 3 unvisited vertex in the list; moreover,if one way is exhausted to continue,also push the first univisited vertex 4 in the list to the queue*/ 5 cout << "BFS of non-oriented Adjacey List:" << endl; 6 srand((unsigned int)time(NULL)); 7 int sze = listVertex.size(); 8 int rdm = rand() % sze;//[0,sze) 9 while (listVertex[rdm]->nextEdgeNode.empty()) { 10 rdm = rand() % sze;//randomly choose a vertex whose out degree is not 0 11 } 12 queue<Vertex*> myQueue; 13 if (startFrom == -1) {//default treatment is random choose 14 myQueue.push(listVertex[rdm]); 15 listVertex[rdm]->color = 2; 16 } 17 else {//designated choose 18 myQueue.push(listVertex[startFrom - 1]); 19 listVertex[startFrom - 1]->color = 2; 20 } 21 while (!myQueue.empty()) {// travel through until there is nothing in the queue 22 Vertex* V = myQueue.front(); 23 V->color = 1; //O black(unvisited) & 1 white(visited) & 2 gray(now in queue)//V visited white 1 24 cout << "Vertex visited:" << V->id + 1 << endl; 25 for (auto it = V->nextEdgeNode.begin(); it != V->nextEdgeNode.end(); it++) {//travel through all outgoing vertices 26 if (listVertex[(*it).first - 1]->color !=1&& listVertex[(*it).first - 1]->color !=2){ 27 myQueue.push(listVertex[(*it).first - 1]);//push into queue for next round travel 28 listVertex[(*it).first - 1]->color = 2; 29 } 30 } 31 myQueue.pop(); 32 } 33 }
无向图要简单多了,关键看两个不同之处,一是这里设置了三个颜色(23行),二是while中的内容简洁得多。
至于为什么这里要设置三种状态(未访问0、已访问1、已入队列2),主要是这里的算法如果用两种状态会有问题。假设两种状态(0未访问、1已访问),如果从7开始访问(置1),好,3、4、5依次加入队尾(无状态设置);然后7被弹出,访问3(置1),并把3的所有非1(未访问)的子顶点4、6加入队尾,这里就发现4被重复加入了队列一次,这是不正确的。
while中的逻辑就很简单,每次访问完某顶点之后,把其所有未被访问过、且不在队列中的顶点加入队尾就行了。
输出示例:
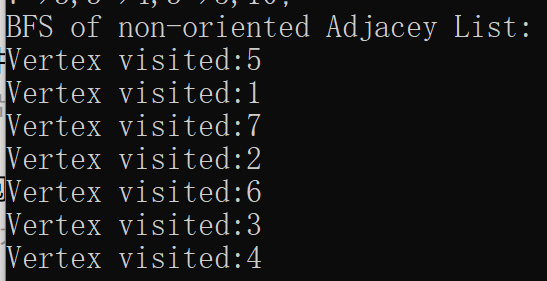
以下是有向图的非递归DFS
1 void Graph::DFSListO(int startFrom) { 2 cout << "Non recursive DFS of oriented Adjacey List:" << endl; 3 srand((unsigned int)time(NULL)); 4 int sze = listVertex.size(); 5 int rdm = rand() % sze;//[0,sze) 6 while (listVertex[rdm]->nextEdgeNode.empty()) { 7 rdm = rand() % sze;//randomly choose a vertex whose out degree is not 0 8 } 9 stack<Vertex*> myStack; 10 Vertex* tempV; 11 int countVisitedAll = 0;//to control overall number of visited vertices 12 if (startFrom == -1) { 13 tempV = listVertex[rdm];//randomly chosed 14 } 15 else 16 { 17 tempV = listVertex[startFrom - 1];//designated 18 } 19 tempV->color = 1;//O black(unvisited) & 1 white(visited) 20 cout << "Vertex visited:" << tempV->id + 1 << endl; 21 myStack.push(tempV); 22 countVisitedAll++; 23 while (!myStack.empty()) { 24 tempV = myStack.top(); 25 int countVisited = 0;//to control number of visited vertices of one certain vertex 26 for (auto it = tempV->nextEdgeNode.begin(); it != tempV->nextEdgeNode.end(); it++) { 27 if (listVertex[(*it).first-1]->color==0) {//if an unvisited vertex has been found 28 listVertex[(*it).first - 1]->color = 1;//O black(unvisited) & 1 white(visited) 29 cout << "Vertex visited:" << listVertex[(*it).first - 1]->id + 1 << endl; 30 myStack.push(listVertex[(*it).first - 1]);//visit it and push into stack 31 countVisitedAll++; 32 break; 33 } 34 else//if a visited vertex found 35 { 36 countVisited++;//then increment the count 37 } 38 } 39 if (countVisited == tempV->nextEdgeNode.size()) { 40 myStack.pop(); 41 } 42 if (countVisitedAll != listVertex.size() && myStack.empty()) { 43 for (auto it = listVertex.begin(); it != listVertex.end(); it++) 44 if ((*it)->color == 0) { 45 (*it)->color = 1;//O black(unvisited) & 1 white(visited) 46 cout << "Vertex visited:" << (*it)->id+ 1 << endl; 47 countVisitedAll++; 48 myStack.push(*it); 49 break; 50 } 51 } 52 } 53 }
使用栈作为辅助数据结构,所有的顶点在访问后被压入栈中。当当前顶点的所有邻接顶点都已被访问时,弹出当前顶点(39-40行);当其还有邻接顶点未被访问时,则从第一个未被访问的顶点开始访问,并将其入栈(26-32行,注意break)。另外对于有向图DFS要考虑到一种情况,就是非强连通图(测试用图就是非强连通图)的问题:如果从初始选择的顶点开始进行DFS,在遍历完他所在的连通分量之后,栈中所有元素都将被弹出,这时如果不作处理,遍历就会结束,这是错误的(如图中从4开始的话,访问完4、7、5就结束)。42-49行做的,就是在访问完其中一个连通分量后,按顺序选择一个未访问过的顶点,访问之,并入栈。这样保证了算法的通用性。
输出示例:
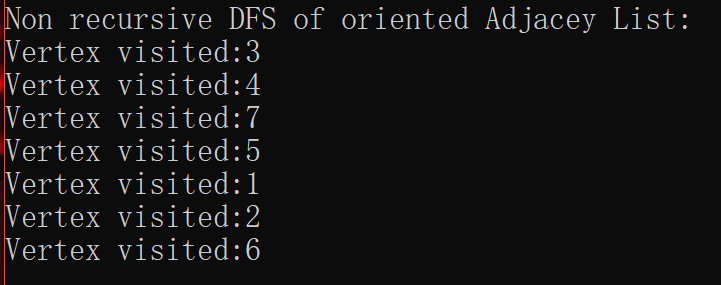
最后一个是递归的无向图DFS
1 void Graph::DFSListN(int startFrom) { 2 cout << "Recursive DFS of non-oriented Adjacey List:" << endl; 3 srand((unsigned int)time(NULL)); 4 int sze = listVertex.size(); 5 int rdm = rand() % sze;//[0,sze) 6 while (listVertex[rdm]->nextEdgeNode.empty()) { 7 rdm = rand() % sze;//randomly choose a vertex whose out degree is not 0 8 } 9 Vertex* tempV; 10 if (startFrom == -1) 11 tempV = listVertex[rdm]; 12 else 13 tempV = listVertex[startFrom - 1]; 14 if (tempV->color == 0) {//not visited 15 tempV->color = 1;//O black(unvisited) & 1 white(visited) 16 cout << "Vertex visited:" << tempV->id+1 << endl; 17 for (auto it = tempV->nextEdgeNode.begin(); it != tempV->nextEdgeNode.end(); it++) { 18 if (listVertex[(*it).first - 1]->color == 0) { 19 DFSListN((*it).first); 20 } 21 } 22 } 23 }
无向图的递归真的很简单哦,每次递归时,tempV都指向前一次访问的顶点的第一个未访问邻接顶点;当tempV已经没有未访问的邻接顶点时,退出本次递归(相当于非递归中的顶点出栈)。
输出示例:(由于递归,输出有点难看)
总结:编程、尤其是算法,是需要经常训练的····一切纸上谈兵都是没用的。另外对于这些图的算法,脑子里想不清楚建议拿出纸笔,把一步步的步骤写出来、画出来,会提高效率。写下这篇博客,加深记忆。
文中如有谬误,敬请读者指出,谢谢!