1. word embedding
在NLP领域,首先要把文字或者语言转化为计算机能处理的形式。一般来说计算机只能处理数值型的数据,所以,在NLP的开始,有一个很重要的工作,就是将文字转化为数字,把这个过程称为 word embedding。
word embedding即词嵌入,就是将一个词或者特征转化为一个向量。
词嵌入一般有两种方式:最简单和原始的方式one-hot;word2vec方式。下面我们简单回顾一下one-hot方式,重点讲解word2vec词嵌入方式。
2. one-hot
one-hot的思想很简单,其长度为字典大小,每个维度对应一个字典里的每个词,除了这个词对应维度上的值是1,其他元素都是0。One-hot vector虽然简单,但是用处有限。当特征数量比较大的时候,one-hot向量就会很长。对于线性的分类器还好,但是模型一旦更加复杂,计算的复杂度就会很快的增长到我们无法承受的程度。同时,由于特征向量中不同维度之间是完全无关的,这就会导致特征向量无法刻画单词间的相似性,从而导致模型的泛化能力较差。
3. word2vec
word2vec 也是word embedding的一种,它会将一个词映射到一个固定维度的向量中(不随语料的变化而变化),并且能够在一定程度上反映出词与词之间的关系。Word2vec是一个用于处理文本的双层神经网络。它的输入是文本语料,输出则是一组向量:该语料中词语的特征向量。虽然Word2vec并不是深度神经网络,但它可以将文本转换为深度神经网络能够理解的数值形式。
word2vec目前主要有两种模型,分别叫做 Skip-gram 和 CBOW。从直观上理解,Skip-Gram是给定input word来预测上下文。而CBOW是给定上下文,来预测input word。接下来会分别介绍下这两种模型的大体思想。
word2vec主要的实现方式有两种,分别为 Hierarchical Softmax 和 Negative sampling。他们和 CBOW 、 skip-gram 两两结合,共可以组成4种不同的模型。我们对基于Hierarchical Softmax的两种模型进行原理分析。
3.1 Skip-gram
skip-gram 主要实现方式就是,通过输入一个词x,预测它的上下文的词。
文本信息:“我”, “想”, “学习”, “计算机”, “技术”
在这个例子中,就相当于当输入“学习”这个词的时候,要输出“我”,“想”,“计算机”,“技术”四个词(假设设定的窗口大小为5)。 具体结构如下图所示:

3.2 CBOW
CBOW 的思想则和skip-gram相反,它是通过上下文的词,去预测当前的词。
文本信息:“我”,“想”,“学习”,“计算机”,“技术”
在这个例子中,就相当于输入为上文“我”,“想”,和下文“计算机”,“技术”,要输出“学习”这个词(假设设定的窗口大小为5)。 具体结构如下:

3.3基于 Hierarchical Softmax 的 CBOW 实现方式及原理

该模型主要由3层组成
1) 第一层:
每一个输入项表示上下文中的词的2c个向量(假设窗口大小为5,则有4个输入,即c=2)
每个输入变量为一个m维的向量,即对应输入的词的词向量
2)第二层:
将上一层输入的2c个向量求和累加
3) 第三层:
输出层,输出为一个二叉树(Huffman树),对应一个叶子节点(每个叶子节点对应一个词,所以叶子节点共有D个,D表示词的种类数量)
那么输出层为什么要输出一个二叉树,以及它是怎么输出的一个二叉树。下面举一个例子:
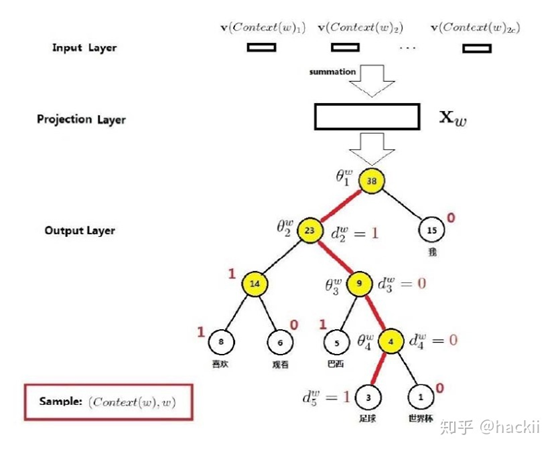
当要输出 足球 这个词的时候,这个模型其实并不是直接输出 "1001" 这条路径,而是在每一个节点都进行一次二分类。
相当于将最后输出的二叉树变成多个二分类的任务。而路径中的每个根节点都是一个待求的向量。 也就是说这个模型不仅需要求每个输入参数的变量,还需要求这棵二叉树中每个非叶子节点的向量,当然这些向量都只是临时用的向量。
所以计算过程可以表示为概率的累乘。 分类的单元使用的是逻辑回归,公式如下:
被分为正类的概率:
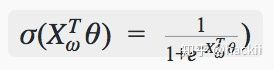
被分为负类的概率:
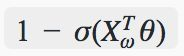
上面公式中的θ即为二叉树中非叶子节点的临时参数。
以“足球”为例,从根节点到叶子节点要经过4个分类器,分别为:
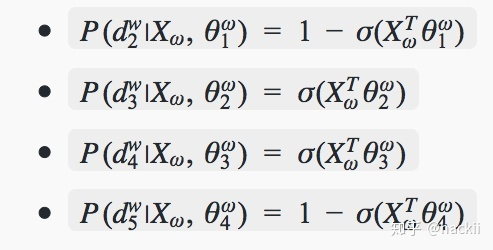
所以可得到:

完整的公式可以表示为:

根据上面的公式可以得到对数似然函数为:

然后通过随机梯度上升法进行训练,更新输入的w
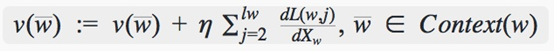
通过不断的计算和更新,最终得到的word2vec模型。
3.4基于 Hierarchical Softmax 的 Skip-gram 实现方式及原理
Skip-gram 的模式跟 CBOW 的基本一样,所以会结合上面的简略的说明一下。
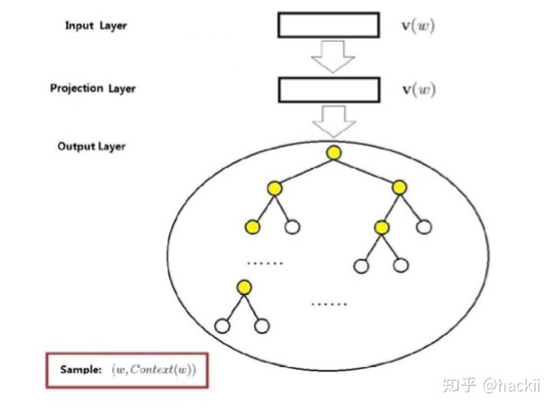
同样也是由3层组成的。唯一的区别就是将第一层输入层输入变量从输入2c个值变为输入一个值。
Skip-gram的模型定义为:
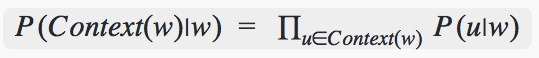
即输出的所有上下文的概率之积。
在这里 P(u∣w)的计算方式就是跟CBOW中说到的一样。
所以可以得到最终的对数似然函数为:

接下来就是跟上面一样的使用随机梯度上升的方式,不断更新各项参数。最终得到最终的word2vec模型。

参考资料
https://www.read138.com/archives/732/f13js0re9wu6zyi7/
https://www.cnblogs.com/DjangoBlog/p/7903683.html
Mikolov T, Sutskever I, Chen K, et al.Distributed representations of words and phrases and theircompositionality[C]//Advances in neural information processing systems. 2013:3111-3119.