扫描线算法

先从一道模板题入手吧..
【模板】扫描线
这道题需要我们求n个矩形的面积并。~~ 数据还很变态 ~~
给出这n的矩形的左下角和右上角坐标，~~ ≤10^9 只能用离散化，离散化之后最多到n也就是10^5，能够维持。
怎么做？
for循环？T(LE)M(LE)大套餐等着你 离散化之后循环都要超时还存不下 ~~
先把所有的面积相加再减去重复？~~ 现实点，你做不到 ~~

---

扫描线算法基础就是应对这种问题的。它的思想是分割图形
比如说，有n个矩形组成这张图。

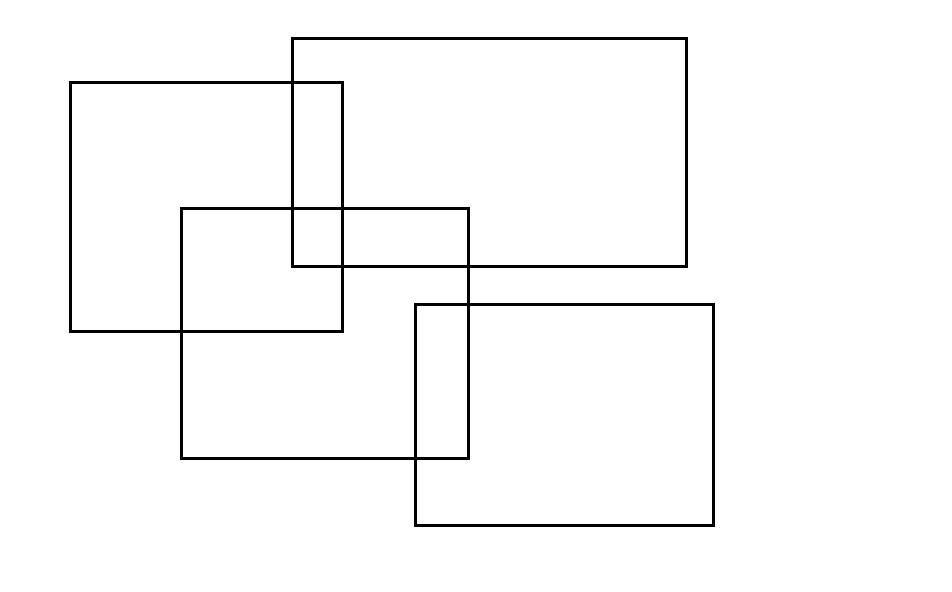
我们设想，有一条无限长度的竖线自左往右扫过这一片图形。只保留这些矩形被竖线扫到的左右两条线段，组成包含2*n条线段的一张图。对于每个矩形，把左边那条线段记为+1，右边的记为-1.
像这样：

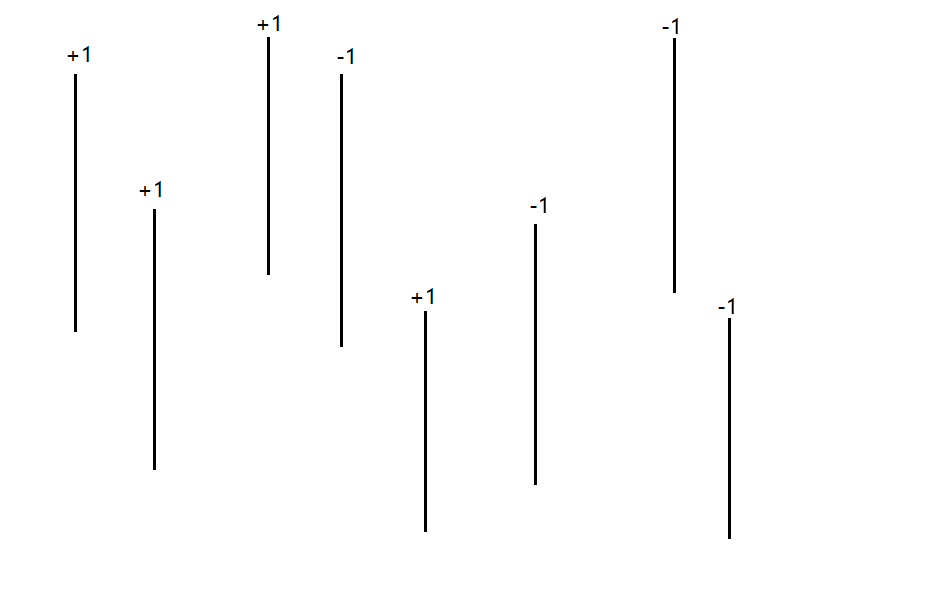
对于两两相邻的部分，我们可以分别计算面积，这样就得到了整个并集图形的面积。
怎么记录这一条条线段？
结构体。要存储的东西有：这条竖线段的横坐标，上下端点的竖坐标，以及1/-1（记录是左还是右）按照题目表述记为：{x,y1,y1,1/-1}
显然，我们只要把这些线的横坐标拿来排序，对于一次遍历来说，每对对应线段之间的距离是已知的，那么我们需要解决的问题只有纵坐标的影响范围。
不妨把所有纵坐标都取出来，离散化映射到[1,t]的区间中的t的整数值，并把这些纵坐标表示为t-1段，其中第i段表示第i个纵坐标和第i+1个纵坐标之间的部分，然后用c[i]表示第i段被覆盖的次数。
这样就可以计算面积并，算法流程大致是这样：

对于每一个线段，将其的k值累加到这个线段对应的若干个纵坐标区间
计算面积：所有T−1个纵坐标区间对应的c值大于零的就说明这些部分的区间还存在，将存在的区间的长度累加起来，乘上当前线段与下一条线段之间的横坐标之差就是这两条线段之间的面积。

---

显然，这里就需要用到区间求和的操作。
这种事情，就丢给线段树吧！

因为这道题中的区间修改都是成对出现的（+1/-1），所以不需要懒标记这个操作。只需要在线段树的每个端点多维护两个值：cnt和len，分别记这段区间被覆盖的次数以及当前区间的纵坐标长度。
算法也很清晰，如果cnt>0，即还有没被的左线段，就更新len为当前区间的纵坐标长度，反之len(k)=len(k2)+len(k2+1)（获取区间纵坐标长度和）。
CODE：

#include<bits/stdc++.h>
using namespace std;
unsigned long long n,t,T,ans,raw[100010<<2],val[100010<<1][2];
inline unsigned long long read()
{
   unsigned long long x=0,f=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){
       if(ch=='-')
           f=-1;
       ch=getchar();
   }
   while(ch>='0'&&ch<='9'){
       x=(x<<1)+(x<<3)+(ch^48);
       ch=getchar();
   }
   return x*f;
}
struct line
{
	unsigned long long x,d,u;
	unsigned long long flag;
	line(){};
	line(int xx,int dd,int uu,int ff)
	{
		x=xx,d=dd,u=uu,flag=ff;
	}
}a[100010<<1];
struct node
{
	unsigned long long l,r,cnt;
	unsigned long long len;
}v[100010<<3];
inline bool cmp(line p1,line p2)
{
	return p1.x<p2.x;
}
inline void input()
{
	unsigned long long x1,y1,x2,y2;
	for(unsigned long long i=1;i<=n;i++)
	{
		x1=read(),y1=read(),x2=read(),y2=read();
		a[2*i-1]=line(x1,y1,y2,1);
		a[2*i]=line(x2,y1,y2,-1);
		raw[++t]=y1,raw[++t]=y2;
	}
	sort(a+1,a+2*n+1,cmp);
	return;
}
inline void dis()
{
	sort(raw+1,raw+1+t);
	t=unique/*去重并返回最后一次去重后的位置*/(raw+1,raw+t+1)-(raw+1);
	for(unsigned long long i=1;i<=2*n;i++)
/*lower_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。*/
		val[i][0]=lower_bound(raw+1,raw+t+1,a[i].d)-raw,
		val[i][1]=lower_bound(raw+1,raw+t+1,a[i].u)-raw;
	return;
}
inline void ud(unsigned long long k)
{
	if(v[k].cnt>0)v[k].len=raw[v[k].r+1]-raw[v[k].l];
	else if(v[k].l==v[k].r)v[k].len=0;
	else v[k].len=v[k<<1].len+v[k<<1|1].len;
}
inline void build(unsigned long long k,unsigned long long l,unsigned long long r)
{
	v[k].l=l,v[k].r=r;
	if(l==r)
	{
		v[l].cnt=v[l].len=0;
		return;
	}
	unsigned long long m=l+(r-l)/2;
	build(k<<1,l,m);
	build(k<<1|1,m+1,r);
	return;
}
inline void modi(unsigned long long k,unsigned long long l,unsigned long long r,unsigned long long de)
{
	if(l<=v[k].l&&r>=v[k].r)
	{
		v[k].cnt+=de;
		ud(k);
		return;
	}
	unsigned long long m=v[k].l+(v[k].r-v[k].l)/2;
	if(l<=m)modi(k<<1,l,r,de);
	if(r>m)modi(k<<1|1,l,r,de);
	ud(k);
	return;
}
inline unsigned long long ask()
{
	return v[1].len;
}
inline void sol()
{
	for(unsigned long long i=1;i<=2*n;i++)
	{
		modi(1,val[i][0],val[i][1]-1,a[i].flag);
		ans+=(a[i+1].x-a[i].x)*ask();
	}
	return;
}
int main()
{
	cin>>n;
	ans=0,t=0;
	input();
	dis();
	build(1,1,t);
	sol();
	cout<<ans;
	return 0;
}