传娃娃
描述
学习空闲之余,小信经常带着同学们做游戏,最近小信发明了一个好玩的新游戏:n 位同学围成一个圈,同学 A 手里拿着一个布娃娃。小信喊游戏开始,每位手里拿着娃娃的同学可以选择将娃娃传给左边或者右边的同学,当小信喊游戏结束时,停止传娃娃。此时手里拿着娃娃的同学即是败者。
玩了几轮之后,小信想到一个问题:有多少种不同的方法,使得从同学 A 开始传娃娃,传了 m 次之后又回到了同学 A 手里。两种方法,如果接娃娃的同学不同,或者接娃娃的顺序不同均视为不同的方法。例如 1->2->3->1和 1->3->2->1 是两种不同的方法。
输入
输入一行,输入两个整数 n,m(3≤n≤30,1≤m≤30),表示一共有 n 位同学一起游戏,一共传 m 次娃娃。
输出
输出一行,输出一个整数,表示一共有多少种不同的传娃娃方法。
输入样例 1
3 3
输出样例 1
2
这道题初一看好像真的想不出该怎么做,但是在同机房大佬的提醒下 应该用DP!
然后就想状态转移方程。。这就炸了。实在想不出该咋玩。于是我试着去画图。(别嫌弃摸鱼酱的图丑)
就以n=6时为例。
初始状态: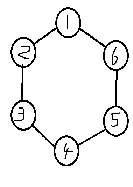
我们用dp[m][n]表示第m次传递后第n个小朋友的传娃娃方法数,很明显,我们需要求的即是dp[m][1]的值。找到边界值:dp[0][1]=1;然后可以发现,一个状态转移方程是无法解决这个比较复杂的dp的,需要添加if语句达到效果。
于是我开始讨论有哪些可能。因为这道题是直接用的dp,并没有构建环,所以这是需要特殊考虑的。然后,我们发现,第i次传递后的点k的方案数,只能由第i-1次传递后的点k的左右两人的方案数之和来得到!原理如下图!

但是如上所述,当这个点是1或n时需要特判,所以情况分为三种:
①这个点是1时:dp[i][j]=dp[i-1][j+1]+dp[i-1][n];
②这个点是n时:dp[i][j]=dp[i-1][j-1]+dp[i-1][1];
③这个点是普通点(非1非n时):dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1];
然后双重循环,外层1…->m,内层1…->n,完事输出dp[m][1]即可。
AC代码如下:
#include<bits/stdc++.h>
using namespace std;
int dp[31][31];
int main()
{
int n,m;
cin>>n>>m;
dp[0][1]=1;
for (int i=1;i<=m;i++)
{
for (int j=1;j<=n;j++)
{
if (j==n)
{
dp[i][j]=dp[i-1][j-1]+dp[i-1][1];
}
else if(j==1)
{
dp[i][j]=dp[i-1][j+1]+dp[i-1][n];
}
else
{
dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1];
}
}
}
cout<<dp[m][1]<<endl;
return 0;
}
ov.