魔法森林[NOI2014]

时间限制: 2 Sec  内存限制: 512 MB

题解

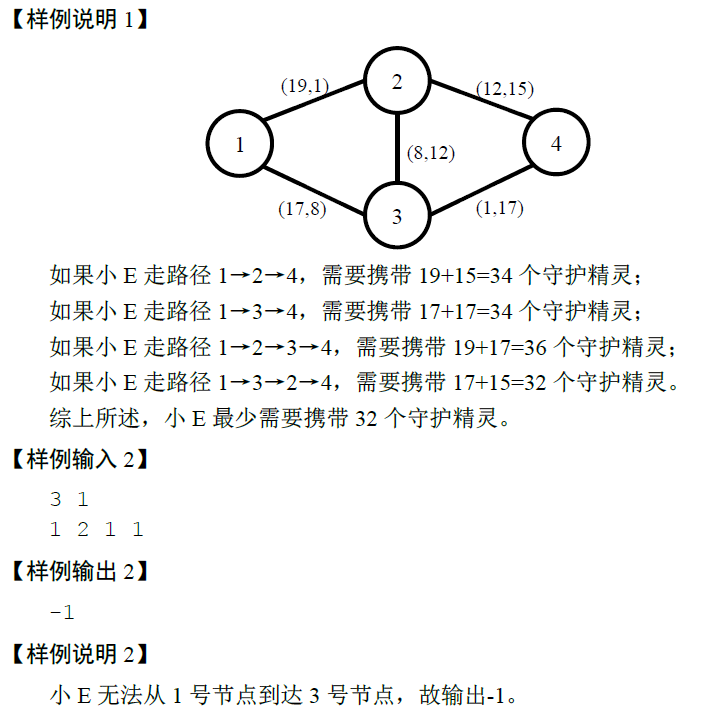
      对于NOI的题已经产生了一种崇敬……因为多半是很锻炼思维能力的题，想出来很困难，实现的过程却乐在其中。这道题大概可以看做最短路问题，但是麻烦之处在于有两个参数，而且要求的最值是两参数之和。据说正解是LCT？并没有学过，等将来有一天能学到的话再来补一发正解吧~

       有一种有理有据、非常可行的方法可以解决掉这道题。把它看做一个类似于生成树的问题来解决(就像前两天的考试题《tarvel》一样逐步建图)，先把边按照a的大小排序，每一次都把权值相等的边一起加入邻接表中，把边的两个端点放入队列。然后跑spfa，求到终点的路上b最大值的最小值（并没有什么不对2333），每一次终点的dis被更新都是因为当前新加入的边的缘故，所以比较刚刚加进去的边的权值+dis[n]与结果的大小，这样就能非常巧妙地解决问题了。

       实现的时候又因为一点边界问题卡了半天。如果每一次都按照这条边和上一条边是否相等来确定同一权值的边是否已经被加完的话，最后加入的一组边就被忽略了。这种小问题总是出错，必须要更细心些。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int sj=100010;
queue<int> q;
int n,m,h[sj>>1],e,dis[sj>>1],ans,tp;
bool r[sj>>1];
struct YB
{
    int xi,yi,ai,bi;
    inline void in()
    {
       scanf("%d%d%d%d",&xi,&yi,&ai,&bi);
    }
}yb[sj];
int comp(const YB&a,const YB&b)
{
    return a.ai<b.ai;
}
struct B
{
    int ne,v,w;
}b[sj*2];
void bj(int &x,int y)
{
     x=x<y?x:y;
}
int ma(int x,int y)
{
     return x>y?x:y;
}
void add(int x,int y,int z)
{
     b[e].v=y;
     b[e].w=z;
     b[e].ne=h[x];
     h[x]=e++;
}
void spfa()
{
     int st;
     while(!q.empty())
     {
        st=q.front();
        q.pop();
        r[st]=0;
        for(int i=h[st];i!=-1;i=b[i].ne)
           if(dis[b[i].v]>ma(b[i].w,dis[st]))
           {
             dis[b[i].v]=ma(b[i].w,dis[st]);
             if(!r[b[i].v])
             {
                q.push(b[i].v);
                r[b[i].v]=1;
             }
           }
     }
}
int main()
{
    scanf("%d%d",&n,&m);
    tp=1;
    for(int i=1;i<=m;i++)
    { 
       yb[tp].in();
       if(yb[tp].xi==yb[tp].yi) tp--;
       tp++;
    }
    m=tp-1;
    sort(yb+1,yb+m+1,comp);
    memset(dis,0x3f,sizeof(dis));
    dis[1]=0;
    ans=0x7fffffff;
    tp=ans;
    memset(h,-1,sizeof(h));
    for(int i=1;i<=m;i++)
    {
       if(yb[i].ai==yb[i-1].ai) continue;
       for(int j=i;j<=m;j++)
       {
          if(yb[i].ai==yb[j].ai)
          { 
             add(yb[j].xi,yb[j].yi,yb[j].bi);
             add(yb[j].yi,yb[j].xi,yb[j].bi);
             if(!r[yb[j].xi]) q.push(yb[j].xi),r[yb[j].xi]=1;
             if(!r[yb[j].yi]) q.push(yb[j].yi),r[yb[j].yi]=1;
          }
          else break; 
       }
       int temp=dis[n];
       spfa();
       if(dis[n]!=temp) bj(ans,dis[n]+yb[i].ai);
    }
    if(ans==tp) printf("-1
");
    else printf("%d",ans);
    return 0;
}