题目描述
1、 每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图6 到图7);如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图1 和图2);
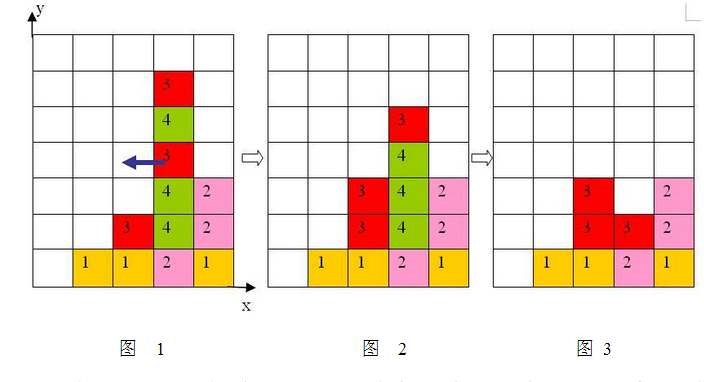
2、 任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图4,三个颜色为1 的方块和三个颜色为2 的方块会同时被消除,最后剩下一个颜色为2 的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,5 个方块会同时被消除)。

3、 方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图1 到图3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0, 0),将位于(3, 3)的方块向左移动之后,游戏界面从图1 变成图2 所示的状态,此时在一竖列上有连续三块颜色为4 的方块,满足消除条件,消除连续3 块颜色为4 的方块后,上方的颜色为3 的方块掉落,形成图3 所示的局面。
输入
第一行为一个正整数n,表示要求游戏通关的步数。
接下来的5 行,描述7*5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个0 结束,自下向上表示每竖列方块的颜色编号(颜色不多于10 种,从1 开始顺序编号,相同数字表示相同颜色)。
输入数据保证初始棋盘中没有可以消除的方块。
输出
如果没有解决方案,输出一行,包含一个整数-1。
样例输入
3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0
样例输出
2 1 1
3 1 1
3 0 1
提示
按箭头方向的顺序分别为图6 到图11
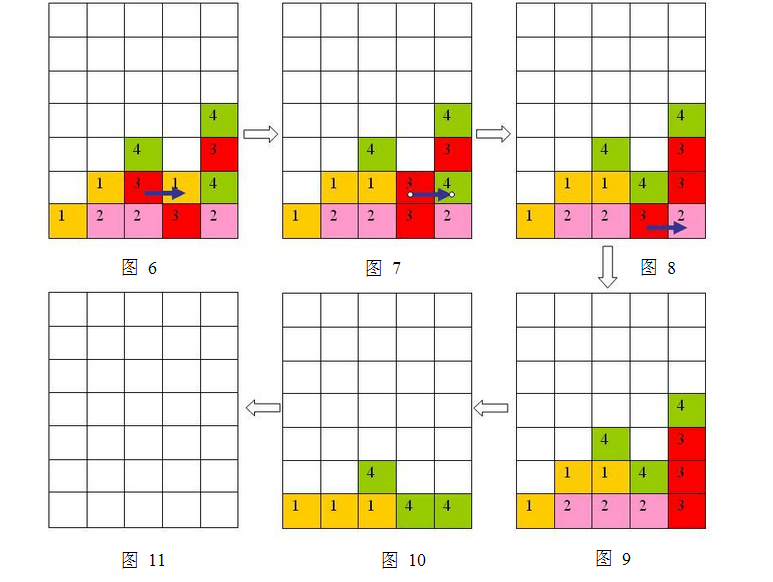
样例输入的游戏局面如上面第一个图片所示,依次移动的三步是:(2,1)处的方格向右移动,(3,1)处的方格向右移动,(3,0)处的方格向右移动,最后可以将棋盘上所有方块消除。
【数据范围】
对于30%的数据,初始棋盘上的方块都在棋盘的最下面一行;
对于100%的数据,0 < n≤5。
【题解】
昨天考试简直迷之做题状态啊。读完题,打了两个暴力,毫无预兆地开始肚子疼,几乎坐不住,趴了多半个上午,后来头晕,莫名还很困。还是不想弃疗,然后在演草纸上写来写去,也没打出什么名堂。然后挨到十二点多,非常万念俱灰地交了卷回宿舍躺着。一整天都难受。
玛雅游戏这题明显是个搜索了,但是一开始打算广搜。看图以为是俄罗斯方块,看题发现是开心消消乐= =,要模拟这么个游戏程序还真不容易。想了想像移动玩具那样,拿哈希什么的水一水,但是这道题并没有什么标准状态,存一下全空好像也没什么意义。好像过了很久才发现好像给出了步数,而且应该还是一定的,题目这是整个读错了呀这个。然后发现,好像有步数我也不会搜?终于彻底弃疗,迷失在传参中无法自拔。想象中这样一个程序应该是分区分功能明显,而且非常简洁的。
最后改过的代码,确实是各个部分功能清晰的。特别让我没想到的,是每次dfs之前复制矩阵,便于回溯。消除函数wipe,用bool型标记了全部可消去块之后一起消除,只要有消除块就要重新调用fall函数。下落函数fall,把所有空块下落之后再调用wipe函数。移动函数move,记录每次的移动操作并开始调用fall。深搜函数dfs,直接按规定的字典序从小到大枚举移动块调用move,每次dfs后还原矩阵。只要在dfs里搜到了一个可行解就直接exit(0)结束整个程序,第一个搜到的解就是最优解,最后都没搜到解就是无解了。
值得一提的是,考试时非常让我头疼的传参在这份代码里降到了最少,很麻烦的记录方案也因为dfs只记录当前解变得非常简单。改题的时候fall函数错过,还原矩阵不够及时,减少了枚举左移次数(左边有块的,左移当前块一定不如把左边的块右移优)和相同块次数(交换相同的好像没什么意义)解决了超时问题,最后居然因为从读入开始的边界问题卡了一个多小时(社会生产效率及其低下!),折腾到将近下晚三才改完。大搜索的第二题,感觉很有成就感,也很有意思。希望以后多调几道这样的题,如果比赛遇到搜索题也能有入手点。
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> using namespace std; int n,a[6][8],temp; bool xq[6][8]; void init() { scanf("%d",&n); for(int i=0;i<5;i++) for(int j=0;j<8;j++) { scanf("%d",&a[i][j]); if(a[i][j]==0) break; } } void wipe(); void fall() { for(int i=0;i<5;i++) for(int j=1;j<8;j++) { temp=j-1; while(temp>=0&&!a[i][temp]&&a[i][temp+1]) { a[i][temp]=a[i][temp+1]; a[i][temp+1]=0; temp--; } } wipe(); } bool bd,qk; void wipe() { for(int i=0;i<5;i++) for(int j=0;j<8;j++) if(a[i][j]) { if(i!=0&&i!=4) if(a[i-1][j]==a[i][j]&&a[i][j]==a[i+1][j]) xq[i-1][j]=xq[i][j]=xq[i+1][j]=1; if(j!=0&&j!=6) if(a[i][j-1]==a[i][j]&&a[i][j]==a[i][j+1]) xq[i][j-1]=xq[i][j]=xq[i][j+1]=1; } bd=0; for(int i=0;i<5;i++) for(int j=0;j<8;j++) if(xq[i][j]) a[i][j]=0,xq[i][j]=0,bd=1; if(bd) fall(); } int ax[6],ay[6],ad[6]; void move(int x,int y,int fx,int bs) { if(fx==1) { temp=a[x+1][y]; a[x+1][y]=a[x][y]; a[x][y]=temp; ax[bs]=x; ay[bs]=y; ad[bs]=fx; fall(); } if(fx==-1) { temp=a[x-1][y]; a[x-1][y]=a[x][y]; a[x][y]=temp; ax[bs]=x; ay[bs]=y; ad[bs]=fx; fall(); } } void dfs(int z) { if(z>n) return; if(z==n) { qk=1; for(int i=0;i<5;i++) for(int j=0;j<8;j++) if(a[i][j]) qk=0; if(qk) { for(int i=1;i<=n;i++) printf("%d %d %d ",ax[i],ay[i],ad[i]); exit(0); } return; } int ww[6][8]; memcpy(ww,a,sizeof(a)); for(int i=0;i<5;i++) for(int j=0;j<8;j++) { if(!a[i][j]) break; if(i!=4&&a[i+1][j]!=a[i][j]) { move(i,j,1,z+1); dfs(z+1); memcpy(a,ww,sizeof(ww)); } if(i!=0&&!a[i-1][j]) { move(i,j,-1,z+1); dfs(z+1); memcpy(a,ww,sizeof(ww)); } } } int main() { freopen("mayan.in","r",stdin); freopen("mayan.out","w",stdout); init(); dfs(0); printf("-1"); return 0; }