A. Maximum Square
Description
给出n个长不同,宽为1的矩形。问怎样能摆放出最大的正方形。
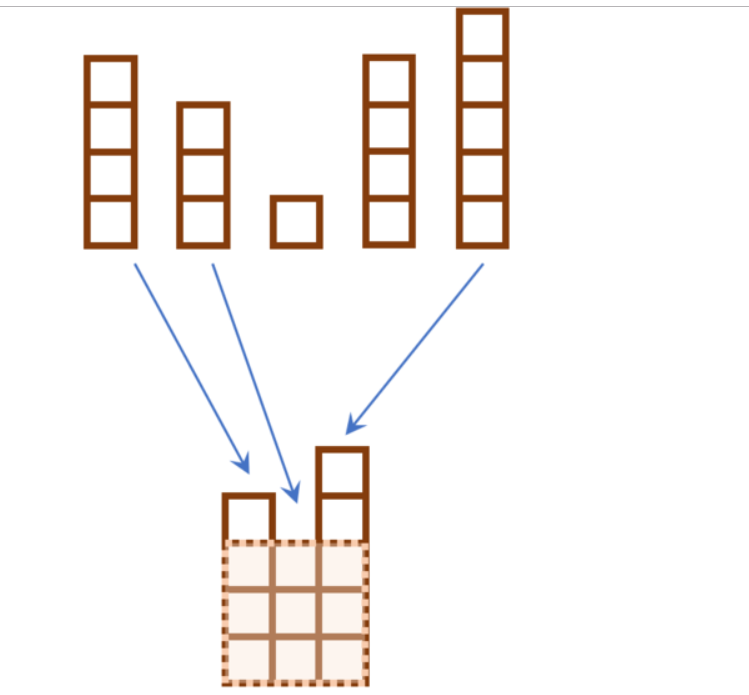
Solution
前缀和模拟求最大值。
B1. Character Swap (Easy Version)
给出两个等长字符串s,t。
可以进行一次操作,swap(s[i],t[j])。
问有无可能s,t相等。
Solution
找出不相等的位置。
如只有一个位置不等或者大于2个位置不等则不可能。
只有两个位置不同的情况特判同一个字符串两位置是否相等。

1 #include <algorithm> 2 #include <cctype> 3 #include <cmath> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <cstring> 7 #include <iostream> 8 #include <map> 9 #include <numeric> 10 #include <queue> 11 #include <set> 12 #include <stack> 13 #if __cplusplus >= 201103L 14 #include <unordered_map> 15 #include <unordered_set> 16 #endif 17 #include <vector> 18 #define lson rt << 1, l, mid 19 #define rson rt << 1 | 1, mid + 1, r 20 #define LONG_LONG_MAX 9223372036854775807LL 21 #define pblank putchar(' ') 22 #define ll LL 23 #define fastIO ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) 24 using namespace std; 25 typedef long long ll; 26 typedef long double ld; 27 typedef unsigned long long ull; 28 typedef pair<int, int> P; 29 int n, m, k; 30 const int maxn = 1e5 + 10; 31 template <class T> 32 inline T read() 33 { 34 int f = 1; 35 T ret = 0; 36 char ch = getchar(); 37 while (!isdigit(ch)) 38 { 39 if (ch == '-') 40 f = -1; 41 ch = getchar(); 42 } 43 while (isdigit(ch)) 44 { 45 ret = (ret << 1) + (ret << 3) + ch - '0'; 46 ch = getchar(); 47 } 48 ret *= f; 49 return ret; 50 } 51 template <class T> 52 inline void write(T n) 53 { 54 if (n < 0) 55 { 56 putchar('-'); 57 n = -n; 58 } 59 if (n >= 10) 60 { 61 write(n / 10); 62 } 63 putchar(n % 10 + '0'); 64 } 65 template <class T> 66 inline void writeln(const T &n) 67 { 68 write(n); 69 puts(""); 70 } 71 template <typename T> 72 void _write(const T &t) 73 { 74 write(t); 75 } 76 template <typename T, typename... Args> 77 void _write(const T &t, Args... args) 78 { 79 write(t), pblank; 80 _write(args...); 81 } 82 template <typename T, typename... Args> 83 inline void write_line(const T &t, const Args &... data) 84 { 85 _write(t, data...); 86 } 87 vector<int> pos; 88 int main(int argc, char const *argv[]) 89 { 90 #ifndef ONLINE_JUDGE 91 freopen("in.txt", "r", stdin); 92 // freopen("out.txt", "w", stdout); 93 #endif 94 fastIO; 95 int t; 96 cin >> t; 97 while (t--) 98 { 99 pos.clear(); 100 cin >> n; 101 string p, q; 102 cin >> p >> q; 103 for (int i = 0; i < n; i++) 104 if (p[i] != q[i]) 105 pos.emplace_back(i); 106 if (pos.size() > 2 || pos.size() == 1) 107 puts("No"); 108 else 109 { 110 int t1 = pos[0], t2 = pos[1]; 111 if (p[t1] == p[t2] && q[t1] == q[t2]) 112 puts("Yes"); 113 else 114 puts("No"); 115 } 116 } 117 return 0; 118 }
B2. Character Swap (Hard Version)
Description
和B1类似,不过最多可以$2n$次操作,如果使得$s=t$输出操作方案。
Solution
首先同一字符总和为偶数一定满足条件,难点只在构造方案。
想到了最多两次交换,没想到把最后位置作为中介,导致编程实现复杂度过高,憨批。
如上一句总结,从前往后扫一遍,如果有$s[i]!=t[i]$
1,在s[i]后面寻找一个位置j满足$s[j]=s[i]$,交换s[j],t[i],若不存在则第2步
2,在t[i]后面寻找一个位置j满足$t[j]=s[i]$,以s[n-1]为中介点,将t[j]交换到t[i]。

1 #include <algorithm> 2 #include <cctype> 3 #include <cmath> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <cstring> 7 #include <iostream> 8 #include <map> 9 #include <numeric> 10 #include <queue> 11 #include <set> 12 #include <stack> 13 #if __cplusplus >= 201103L 14 #include <unordered_map> 15 #include <unordered_set> 16 #endif 17 #include <vector> 18 #define lson rt << 1, l, mid 19 #define rson rt << 1 | 1, mid + 1, r 20 #define LONG_LONG_MAX 9223372036854775807LL 21 #define pblank putchar(' ') 22 #define ll LL 23 #define fastIO ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) 24 using namespace std; 25 typedef long long ll; 26 typedef long double ld; 27 typedef unsigned long long ull; 28 typedef pair<int, int> P; 29 int n, m, k; 30 const int maxn = 1e5 + 10; 31 template <class T> 32 inline T read() 33 { 34 int f = 1; 35 T ret = 0; 36 char ch = getchar(); 37 while (!isdigit(ch)) 38 { 39 if (ch == '-') 40 f = -1; 41 ch = getchar(); 42 } 43 while (isdigit(ch)) 44 { 45 ret = (ret << 1) + (ret << 3) + ch - '0'; 46 ch = getchar(); 47 } 48 ret *= f; 49 return ret; 50 } 51 template <class T> 52 inline void write(T n) 53 { 54 if (n < 0) 55 { 56 putchar('-'); 57 n = -n; 58 } 59 if (n >= 10) 60 { 61 write(n / 10); 62 } 63 putchar(n % 10 + '0'); 64 } 65 template <class T> 66 inline void writeln(const T &n) 67 { 68 write(n); 69 puts(""); 70 } 71 template <typename T> 72 void _write(const T &t) 73 { 74 write(t); 75 } 76 template <typename T, typename... Args> 77 void _write(const T &t, Args... args) 78 { 79 write(t), pblank; 80 _write(args...); 81 } 82 template <typename T, typename... Args> 83 inline void write_line(const T &t, const Args &... data) 84 { 85 _write(t, data...); 86 puts(""); 87 } 88 int a[26], b[26]; 89 string p, q; 90 int main(int argc, char const *argv[]) 91 { 92 #ifndef ONLINE_JUDGE 93 freopen("in.txt", "r", stdin); 94 // freopen("out.txt", "w", stdout); 95 #endif 96 fastIO; 97 int t; 98 cin >> t; 99 while (t--) 100 { 101 memset(a, 0, sizeof a); 102 memset(b, 0, sizeof b); 103 cin >> n; 104 cin >> p >> q; 105 for (int i = 0; i < n; i++) 106 ++a[p[i] - 'a'], ++b[q[i] - 'a']; 107 int f = 1; 108 for (int i = 0; i < 26 && f; i++) 109 if ((a[i] + b[i]) & 1) 110 f = 0; 111 if (f) 112 { 113 puts("Yes"); 114 vector<P> res(0); 115 for (int i = 0; i < n; i++) 116 if (p[i] != q[i]) 117 { 118 int pos = 0; 119 for (int j = i + 1; j < n && !pos; j++) 120 if (p[j] == p[i]) 121 pos = j; 122 if (pos) 123 { 124 res.emplace_back(pos, i); 125 swap(p[pos], q[i]); 126 } 127 else 128 { 129 int pos = 0; 130 for (int j = i + 1; j < n && !pos; j++) 131 if (q[j] == p[i]) 132 pos = j; 133 res.emplace_back(n - 1, pos); 134 res.emplace_back(n - 1, i); 135 swap(p[n - 1], q[pos]); 136 swap(p[n - 1], q[i]); 137 } 138 } 139 int sz = res.size(); 140 writeln(sz); 141 for (int i = 0; i < sz; i++) 142 write_line(res[i].first + 1, res[i].second + 1); 143 } 144 else 145 puts("No"); 146 } 147 return 0; 148 }
C. Tile Painting
Description

Solution
我也太憨了8,上上一场才有类似的唯一分解。
唯一分解后,如果素因子个数大于1则答案为1。
素因子个数等于1答案为素因子。
注意特判$n=1$
考虑n=10,素因子有2,5。
先安排到1,2时可以有两种颜色,但是到6这个点,$(6-4=2)|10,(4-2=2)|10,(6-1=5)|10, ightarrow 1=2=4=6$固只能有一种颜色。
因为$gcd(2,5)=1$,由裴属定理$gcd(a,b)=ax+by$存在整数解,也就是说只要$gcd(a,b)|m$,则m可以由$ax+by$表示。
而只要有两个以上素因子,gcd肯定为1,任意数都可以由素因子倍数表示,答案为1。

1 #include <algorithm> 2 #include <cctype> 3 #include <cmath> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <cstring> 7 #include <iostream> 8 #include <map> 9 #include <numeric> 10 #include <queue> 11 #include <set> 12 #include <stack> 13 #if __cplusplus >= 201103L 14 #include <unordered_map> 15 #include <unordered_set> 16 #endif 17 #include <vector> 18 #define lson rt << 1, l, mid 19 #define rson rt << 1 | 1, mid + 1, r 20 #define LONG_LONG_MAX 9223372036854775807LL 21 #define pblank putchar(' ') 22 #define ll LL 23 #define fastIO ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) 24 using namespace std; 25 typedef long long ll; 26 typedef long double ld; 27 typedef unsigned long long ull; 28 typedef pair<int, int> P; 29 int n, m, k; 30 const int maxn = 1e7 + 10; 31 template <class T> 32 inline T read() 33 { 34 int f = 1; 35 T ret = 0; 36 char ch = getchar(); 37 while (!isdigit(ch)) 38 { 39 if (ch == '-') 40 f = -1; 41 ch = getchar(); 42 } 43 while (isdigit(ch)) 44 { 45 ret = (ret << 1) + (ret << 3) + ch - '0'; 46 ch = getchar(); 47 } 48 ret *= f; 49 return ret; 50 } 51 template <class T> 52 inline void write(T n) 53 { 54 if (n < 0) 55 { 56 putchar('-'); 57 n = -n; 58 } 59 if (n >= 10) 60 { 61 write(n / 10); 62 } 63 putchar(n % 10 + '0'); 64 } 65 template <class T> 66 inline void writeln(const T &n) 67 { 68 write(n); 69 puts(""); 70 } 71 template <typename T> 72 void _write(const T &t) 73 { 74 write(t); 75 } 76 template <typename T, typename... Args> 77 void _write(const T &t, Args... args) 78 { 79 write(t), pblank; 80 _write(args...); 81 } 82 template <typename T, typename... Args> 83 inline void write_line(const T &t, const Args &... data) 84 { 85 _write(t, data...); 86 } 87 int pcnt, vis[maxn], prime[maxn]; 88 void init() 89 { 90 for (int i = 2; i < maxn; i++) 91 { 92 if (!vis[i]) 93 prime[pcnt++] = i; 94 for (int j = 0; j < pcnt && i * prime[j] < maxn; j++) 95 { 96 vis[i * prime[j]] = 1; 97 if (i % prime[j] == 0) 98 break; 99 } 100 } 101 } 102 int main(int argc, char const *argv[]) 103 { 104 #ifndef ONLINE_JUDGE 105 freopen("in.txt", "r", stdin); 106 // freopen("out.txt", "w", stdout); 107 #endif 108 init(); 109 ll n = read<ll>(); 110 if (n == 1) 111 { 112 writeln(1); 113 return 0; 114 } 115 ll res = n; 116 vector<ll> fac; 117 fac.clear(); 118 for (int i = 0; i < pcnt && prime[i] <= n; i++) 119 { 120 int cur = 0; 121 while (n % prime[i] == 0) 122 { 123 ++cur; 124 n /= prime[i]; 125 } 126 if (cur) 127 fac.emplace_back(prime[i]); 128 } 129 if (n > 1) 130 fac.emplace_back(n); 131 ll gcd = 0; 132 int sz = fac.size(); 133 for (int i = 0; i < sz; i++) 134 gcd = __gcd(fac[i], gcd); 135 writeln(gcd); 136 return 0; 137 }
D. 0-1 MST
Description
给出一个n个点的简单完全图。有m条边权值为1,其余边权值为0。
求最小生成树。
Solution
我们肯定得多选权值为0的边构成生成树。
从任一点开始搜索有边相连的权值为0的点,构成连通块。
将n个点缩为m个连通块后,可以知道这些全是权值为0的块。
由于是一个完全图,任意两点没有0边相连,必有1边相连,而连接m个连通块生成最小生成树的权值为m-1条边。
因此答案为m-1。
我用的set实现,在erase的时候注意更新迭代器,不然会re。

1 #include <algorithm> 2 #include <cctype> 3 #include <cmath> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <cstring> 7 #include <iostream> 8 #include <map> 9 #include <numeric> 10 #include <queue> 11 #include <set> 12 #include <stack> 13 #if __cplusplus >= 201103L 14 #include <unordered_map> 15 #include <unordered_set> 16 #endif 17 #include <vector> 18 #define lson rt << 1, l, mid 19 #define rson rt << 1 | 1, mid + 1, r 20 #define LONG_LONG_MAX 9223372036854775807LL 21 #define pblank putchar(' ') 22 #define ll LL 23 #define fastIO ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) 24 using namespace std; 25 typedef long long ll; 26 typedef long double ld; 27 typedef unsigned long long ull; 28 typedef pair<int, int> P; 29 int n, m, k; 30 const int maxn = 1e5 + 10; 31 template <class T> 32 inline T read() 33 { 34 int f = 1; 35 T ret = 0; 36 char ch = getchar(); 37 while (!isdigit(ch)) 38 { 39 if (ch == '-') 40 f = -1; 41 ch = getchar(); 42 } 43 while (isdigit(ch)) 44 { 45 ret = (ret << 1) + (ret << 3) + ch - '0'; 46 ch = getchar(); 47 } 48 ret *= f; 49 return ret; 50 } 51 template <class T> 52 inline void write(T n) 53 { 54 if (n < 0) 55 { 56 putchar('-'); 57 n = -n; 58 } 59 if (n >= 10) 60 { 61 write(n / 10); 62 } 63 putchar(n % 10 + '0'); 64 } 65 template <class T> 66 inline void writeln(const T &n) 67 { 68 write(n); 69 puts(""); 70 } 71 template <typename T> 72 void _write(const T &t) 73 { 74 write(t); 75 } 76 template <typename T, typename... Args> 77 void _write(const T &t, Args... args) 78 { 79 write(t), pblank; 80 _write(args...); 81 } 82 template <typename T, typename... Args> 83 inline void write_line(const T &t, const Args &... data) 84 { 85 _write(t, data...); 86 } 87 set<int> g[maxn], s; 88 int vis[maxn]; 89 void bfs(int x) 90 { 91 s.erase(x); 92 queue<int> q; 93 q.emplace(x); 94 while (!q.empty()) 95 { 96 int now = q.front(); 97 q.pop(); 98 if (vis[now]) 99 continue; 100 vis[now] = 1; 101 for (auto it = s.begin(); it != s.end();) 102 { 103 int v = *it; 104 int f = 1; 105 if (g[now].find(v) == g[now].end()) 106 q.emplace(v), it = s.erase(it), f = 0; 107 if (f) 108 ++it; 109 } 110 } 111 } 112 int main(int argc, char const *argv[]) 113 { 114 #ifndef ONLINE_JUDGE 115 freopen("in.txt", "r", stdin); 116 // freopen("out.txt", "w", stdout); 117 #endif 118 n = read<int>(), m = read<int>(); 119 for (int i = 1; i <= n; i++) 120 s.emplace(i); 121 for (int i = 0; i < m; i++) 122 { 123 int x = read<int>(), y = read<int>(); 124 g[x].emplace(y), g[y].emplace(x); 125 } 126 int res = 0; 127 for (int i = 1; i <= n; i++) 128 if (!vis[i]) 129 bfs(i), ++res; 130 writeln(res - 1); 131 return 0; 132 }
