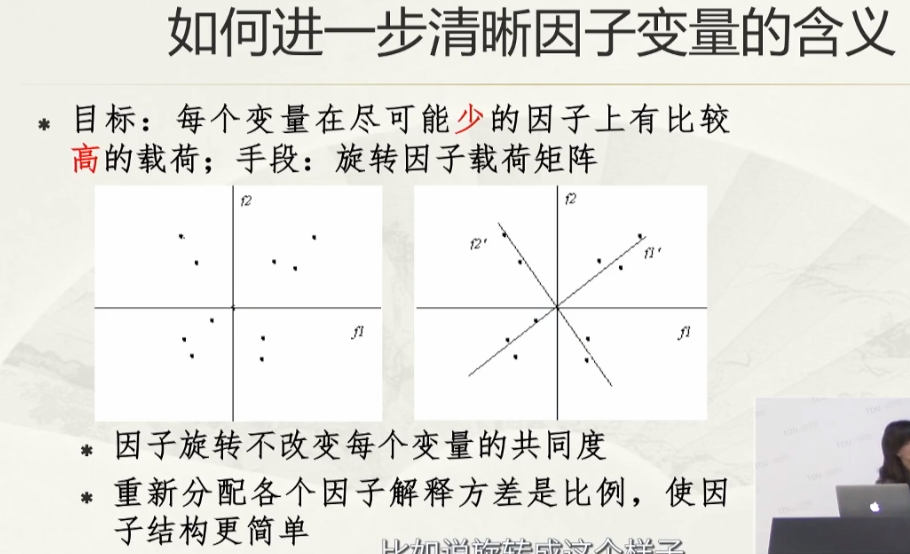
因子分析是将多个实测变量转换为少数几个综合指标(或称潜变量),主要用于寻找数据的内在逻辑和降维。在本课节中,老师从应用因子分析的情境出发,经过方差共同度分析、主成分分析,深入浅出地解析获取公因子的过程,拔高学员的数据处理能力。
本节课包括以下知识点:
-
何种情况进行特征提取
-
因子分析
-
方差共同度
-
主成分分析



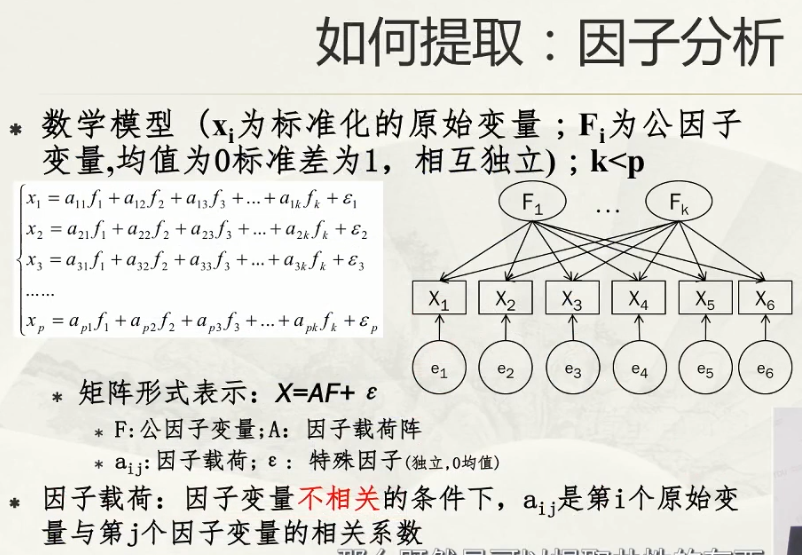
是否遗漏:是否有方差,是否有方差的丢失;
和的方差能够变为方差的和;


列项求和;
怎么去考察原有有没有丢失重要的变量:
一个是从变量的共同度的角度,变量的共同度越接近于1,说明它的方差丢失越少,重要的信息保留的越多;
二,全体变量丢失和保留的情况,可以通过所有变量共同度之和来做,也等价可以用因子变量它的方差贡献之和来做,更直观的方式是用总的方差贡献率来做,这个值越接近于1,说明原有变量它的方差的保留越多;
主成分分析:给因子分析做铺垫;
主成分分析的出现主要是为了降维——即将已知的所有变量只抽取重要的几个变量进行分析;

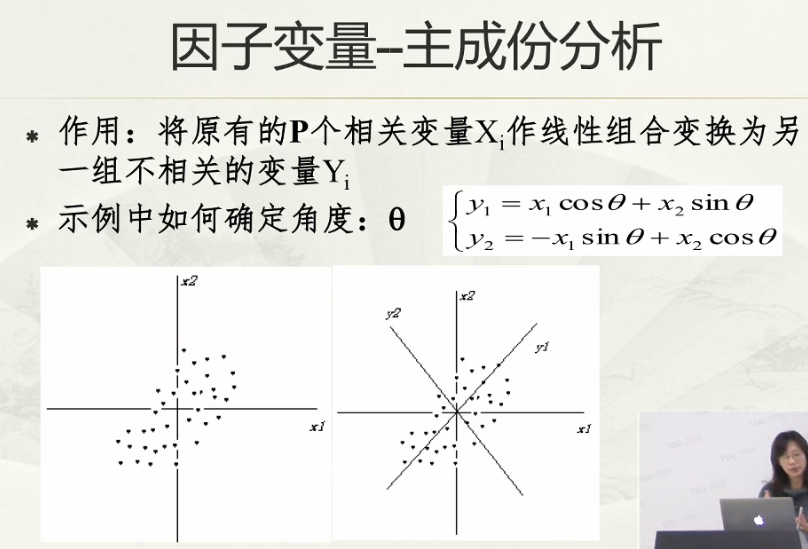
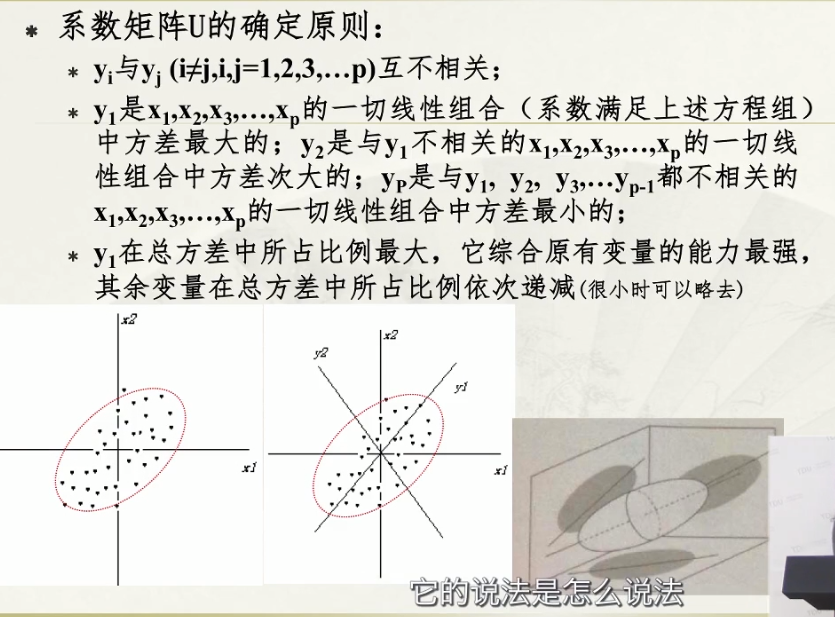
主成分分析中,y1到yp的方差是递减的,所以只需要留最大的几个y作为主成分即可;





只要降维,方差一定会丢失,但是一般都会保证方差贡献率在80%以上;