肉眼可见的 Z 变换性质

本文对双边 Z 变换的部分常见性质做了简要的剖析，希望能展示一种轻松的、形象的理解Z变换性质的方法。

背景

Z 变换究竟在做什么？(X(z)) 究竟代表了什么？

令 (z=re^{jomega})，是一个普普通通的伸扭，那么 (x(n)=z^n) 也就构成了一个基本的信号：每拍在之前一拍位移的基础上多做一个 (z) 的伸扭。显然，离散时间傅里叶变换是 (r=1) 的特例，此时只有伸缩而没有扭转。

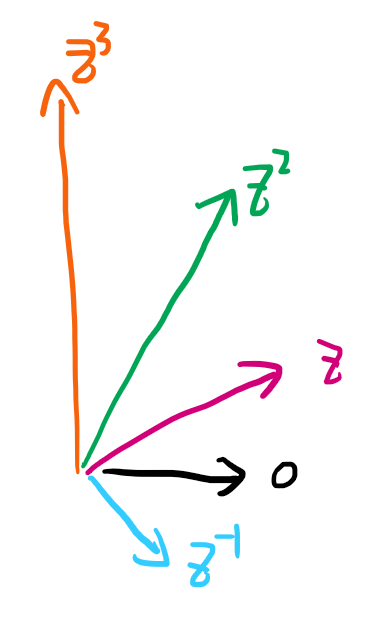
现在 Z 变换要做的事情，就是将一个复杂信号 (x(n))，分解成若干个 (z^n) 的线性组合的形式。其中，(z^n) 分量的多寡（准确还包括相位的偏移），我们用 (X(z)) 来表示，于是，你就得到了一个并不严格的抽象表达

[x(n)=sum_{z} X(z)cdot z^n ]

先不管这玩意怎么算。我们考虑如何求出 (X(z))，你仍然可以借助“投影”或者“相似度”的类比来理解 Z 变换的式子

[X(z)=sum_{n=-infty} ^ infty displaystyle frac {x(n)} {z^n} ]

言归正传，本文我们讨论 Z 变换的性质，也就是我们知道一个家伙的 Z 变换，我们想要轻松地推出一个和它长得很相似的家伙的 Z 变换。结合 Z 变换的意义，我们知道信号 (x(n)) 中任意 (z) 分量的含量（还包括相位偏移），想要推出另一个信号 (x_1(n)) 中任意 (z) 分量的含量。

因此，在形象理解 Z 变换性质的过程中，应当紧扣：信号 (x_1(n)) 中的 (z) 分量，对应着信号 (x(n)) 中的哪些分量？信号 (x(n)) 中的 (z) 分量，在经过一些小修改后，变成了信号 (x_1(n)) 中的什么？更确切地，一个基本单元 (z) 在经过那些小修改后，变成了什么？

时移性质

若 (x(n) leftrightarrow X(z))，则 (x(n-n_0) leftrightarrow displaystyle frac {X(z)} {z^{n_0}})

我们盯住 (x(n)) 中的一个 (z)，现在整个信号延迟了 (n_0) 拍，也就意味着 (x_1(n)=x(n-n_0))，相当于这个基本单元后退 (n_0) 拍，因此它按 (z) 倒转 (n_0) 次，即 (displaystyle frac {X(z)} {z^{n_0}})。

尺度变换/频移特性

因为这里的尺度变化和频移特性本质上是一回事，所以我们放在一起说，直接用一个复频移特性来代替。

若 (x(n) leftrightarrow X(z))，则 (z_0^n x(n) leftrightarrow X(displaystyle frac z {z_0}))

由于我们让整个信号每拍都多做一个 (z_0) 的伸扭，那么现在每拍做 (z) 伸扭的原来每拍做 (displaystyle frac z {z_0}) 的伸扭，所以现在的 (z) 对应着原来的 (displaystyle frac z {z_0})。太轻松了！

这里我们还需要关注这个性质的两个推论，分别是 (|z|=1) 和 (|z|=z) 时的情况，对应着的不妨称作纯频移特性和纯尺度变换特性。

若 (x(n) leftrightarrow X(z))，则 (e^{jomega_0 n} x(n) leftrightarrow X(displaystyle frac z {e^{jomega_0}}))

很简单，每拍多转一个 (omega_0)，对应着原来的就是 (z) 的扭度减少 (omega_0) 的分量。

若 (x(n) leftrightarrow X(z))，则 (r_0^n x(n) leftrightarrow X(displaystyle frac z {r_0}))

同理，每拍多伸展一个 (r_0) 倍，对应着原来的 (z) 的伸缩率减少 (r_0) 倍的分量。

时域反转

若 (x(n) leftrightarrow X(z))，则 (x(-n) leftrightarrow X(z^{-1}))

时域反转，那就让所有基本信号 (z) 反过来转，变成 (z^{-1})。

共轭对称性

若 (x(n) leftrightarrow X(z))，则 (x^*(n) leftrightarrow X^*(z^*))

时域取共轭，对于一个 (z) 来说，无非就是它的旋转方向变了，但是伸缩方向不变。同时，因为 (X(z)) 描述的伸扭代表了 (z) 的量和相，这个初相角，也受共轭影响而取反。因此，不仅需要对 (z) 取共轭，还需要对 (X) 取共轭。

时域内插

首先说说什么是时域内插，它定义为

[x_{(k)}(n) = [k|n]cdot x(frac n k) ]

考虑一个简单的栗子，(x(n)=[1,2,3,4,...])，做 (k=2) 的时域内插，变成 (x_{(2)}(n)=[1,0,2,0,3,0,4,0,...])。

若 (x(n) leftrightarrow X(z))，则 (x_{(k)}(n) leftrightarrow X(z^k))

唔，这个有点费劲。我是否可以模糊地说，一个 (z) 在经过时域内插后，变成了 (z^{frac 1 k})？

所以这里还是最好从式子上看一下，即

[X_k(z)=sum_{n=-infty}^{infty} x(frac n k) z^{-k}=sum_{n=-infty}^{infty} x(n)z^{-nk}=X(z^k) ]

时域卷积

若 (x_1(n)leftrightarrow X_1(n), x_2(n)leftrightarrow X_2(n))，则 (x_1(n) * x_2(n) leftrightarrow X_1(z) cdot X_2(z))

我们已经知道，两个系统的叠加作用在时域上表现为卷积的形式。那么在频域上呢？系统只是对一个基本信号 (z) 提供一个伸扭，那么自然，两个系统的合作用就是它们伸扭的叠加。

时域求和性质就是时域卷积性质的推论，在这里不做赘述。

z域微分特性

若 (x(n) leftrightarrow X(z))，则 (nx(n) leftrightarrow -z displaystyle frac {dX(z)} {dz})

这个真的不好说。只能大概说，对序列做 (n) 的线性加权后，频域中关于 (z) 的变化特性被凸显出来？

初值/终值定理

初值定理描述了对于因果序列，根据 Z 变换求时域初值的方式

若 (x(n) leftrightarrow X(z))，则 (x(0)=displaystyle lim_{z o infty} X(z))

初值定理是非常直观的，盯住 Z 变换的定义，

[X(z)=x(0)+sum_{n=1}^infty frac {x(n)} {z^n} ]

当 (z o infty) 后，只有 (n=0) 时我们才能取得对答案有贡献的值。

事实上，我们可以稍作修改，

[z(X(z)-x(0))=x(1) + zsum_{n=2}^infty frac {x(n)} {z^n} ]

类似这样，我们可以求出任意拍 (n) 时的 (x(n))，即

[x(n) = lim_{z o infty} z^n [X(z)-sum_{k=0}^{n-1} frac {x(k)} {z^k}] ]

类似初值定理，当 (x(n)) 的终止存在时，有终值定理

若 (x(n) leftrightarrow X(z))，则 (x(infty)=displaystyle lim_{z o1} [(z-1)X(z)])

上面我们省略了一些条件。在初值定理中要求极限存在。在终值定理中，要求 (X(z)) 除了 (z=1) 处最多有一个一阶极点，其他极点都必须在单位圆内。