为什么需要残差网络
退化问题
随着网络深度的增加,准确度变得饱和然后迅速退化。这种退化不是由过度拟合引起的,并且在适当的深度模型中添加更多层会导致更高的训练误差。

如下图所示
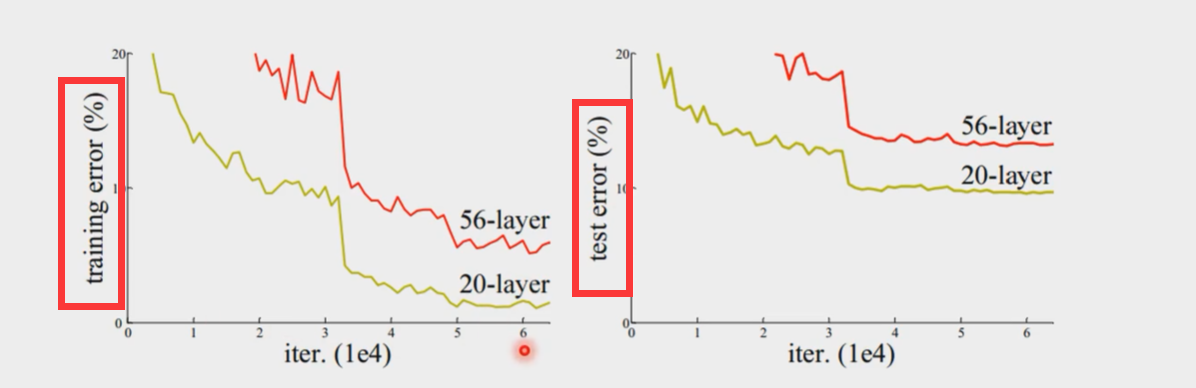
20层的神经网络不论是在训练还是测试中都比56层的错误率更低误差更低,且不是因为过拟合导致的问题
反向传播
反向传播(用于优化神网参数):根据损失函数计算的误差通过反向传播的方式,指导深度网络参数的更新优化。
采取反向传播的原因:首先,深层网络由许多线性层和非线性层堆叠而来,每一层非线性层都可以视为是一个非线性函数(非线性来自于非线性激活函数),因此整个深度网络可以视为是一个复合的非线性多元函数。
最终的目的是希望这个非线性函数很好的完成输入到输出之间的映射,也就是找到让损失函数取得极小值。所以最终的问题就变成了一个寻找函数最小值的问题,在数学上,很自然的就会想到使用梯度下降来解决。
梯度消失
当梯度消失发生时,接近于输出层的隐藏层由于其梯度相对正常,所以权值更新时也就相对正常,但是当越靠近输入层时,由于梯度消失现象,会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时,只等价于后面几层的浅层网络的学习。
通俗来说
在神经网络中,当前面隐藏层的学习速率低于后面隐藏层的学习速率,即随着隐藏层数目的增加,分类准确率反而下降了。
前面的隐藏层的学习速度要低于后面的隐藏层。这种现象普遍存在于神经网络之中叫做梯度消失
残差网络
跨层
跨过权重层和激活函数,直接跨层连接
x是输入(上一步模块的输出),H(X)是输出
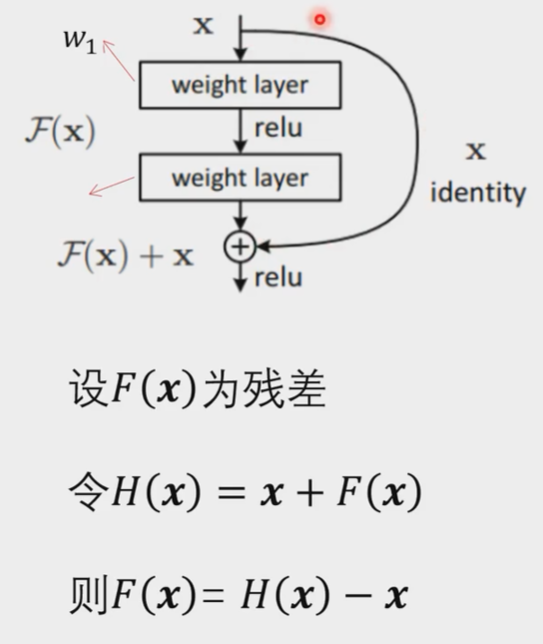
当输入维度和输出维度相同的时候,可跨层(如果权重影响不大的话)
当输入维度和输出维度不同的时候,做线性变换

资料来源
统计计算与机器学习6: 生成对抗网络GAN,残差网络Resnet,图卷积网络GCN_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili