【模板】三分查找

三分查找和二分查找差不多，就是把一段区间平均分成三段而不是两段。

三分查找适用于凸函数，即有一个顶点，顶点两边单调的函数（比如二次函数）。

对于一段l~r的区间，把它分成l~L，L~R，R~r三段。

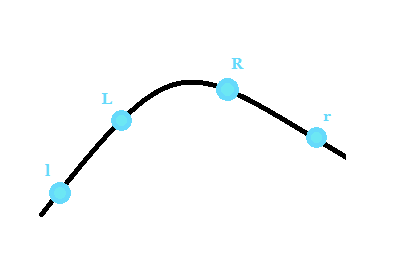
以顶点为最大值的情况为例，

若f(L)<f(R)，则最高点在L~R或R~r中。

若f(L)>f(R)，则最高点在l~L或L~R中，

while(r-l>=1e-6) {
    double k = (r-l)/3.0;
    double L = l+k;
    double R = r-k;
    if(f(L) < f(R)) l = L;
    else r = R;
}
printf("%.5lf",l);

例题：Luogu 3382 【模板】三分法

PS:关于多项式的求法，有一个简单算法叫秦九韶算法。

例子:

　$10x^5+9x^4+8x^3+7x^2+6x+5$

$=x(10x^4+9x^3+8x^2+7x+6)+5$

$=x(x(10x^3+9x^2+8x+7)+6)+5$

$=x(x(x(10x^2+9x+8)+7)+6)+5$

$=x(x(x(x(10x+9)+8)+7)+6)+5$

$=x(x(x(x(x(10)+9)+8)+7)+6)+5$

用代码写起来就是这样qwq

ans = 0;
for(int i = 0; i <= n; i++)
    ans = ans*x+a[i];

然后..这道题的完整代码如下

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#define MogeKo qwq
using namespace std;
int n;
double a[15],l,r;

double f(double x){
    double ret = 0;
    for(int i = 0;i <= n;i++)
        ret = ret*x+a[i];
    return ret;
}

int main(){
    scanf("%d%lf%lf",&n,&l,&r);
    for(int i = 0;i <= n;i++)
        scanf("%lf",&a[i]);
    while(r-l>=1e-6){
        double k = (r-l)/3.0;
        double L = l+k;
        double R = r-k;
        if(f(L) < f(R)) l = L;
        else r = R;
    }
    printf("%.5lf",l);
    return 0;
}