定义
栈是一种限定仅在表尾进行插入或删除操作的线性表。允许插入或删除的一端为栈顶,另一端为栈底。特点是先进后出( first in last out )。栈的插入操作叫做入栈,栈的删除操作叫做出栈。
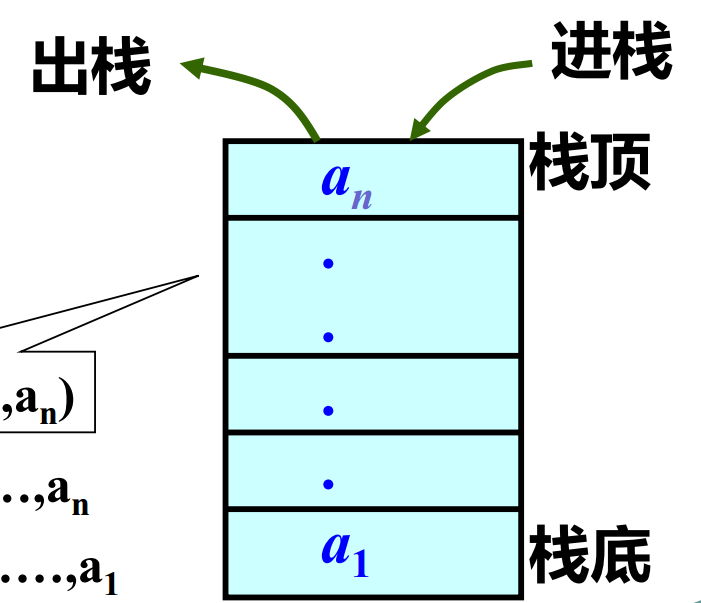
结构表示
typedef int Elemtype; typedef struct { Elemtype data[size]; int top; } Stack;
操作集及实现
/**
*C语言
*/
入栈
int push( Stack *s , Elemtype e ) { if( s->top == size - 1 ) { return 0; } s->top++; s->data[s->top] = e; return 1; }
把指针加1,接着给栈顶赋值。
出栈
int pop( Stack *s , Elemtype *e ) { if( s->top == -1 ) { return 0; } *e = s->data[s->top]; s->top--; return 1; }
指针减1,将栈顶元素出栈,本质上只是移动指针,并没有将栈顶元素销毁,而是会在入栈的时候将其内容覆盖。
遍历
void display( Stack *s ) { int i; for( i = 0 ; i <= s->top ; i++ ) { printf("%d ",s->data[i]); } printf(" "); }
全部代码
#include<stdio.h> #define size 20 //栈的结构 typedef int Elemtype; typedef struct { Elemtype data[size]; int top; } Stack; //操作集 //初始化 void init( Stack *s ) { s->top = -1; } //入栈操作 int push( Stack *s , Elemtype e ) { if( s->top == size - 1 ) { return 0; } s->top++; s->data[s->top] = e; return 1; } //出栈操作 int pop( Stack *s , Elemtype *e ) { if( s->top == -1 ) { return 0; } *e = s->data[s->top]; s->top--; return 1; } void display( Stack *s ) { int i; for( i = 0 ; i <= s->top ; i++ ) { printf("%d ",s->data[i]); } printf(" "); } int main() { Stack L; int n; init(&L); push(&L,5); push(&L,6); push(&L,7); display(&L); pop(&L,&n); display(&L); pop(&L,&n); display(&L); return 0; }