高等数理统计（三）

引言

　　【比较官方的简介】数理统计学是一门以概率论为基础，应用性很强的学科。它研究怎样以有效的方式收集、 整理和分析带有随机性的数据，以便对所考察的问题作出正确的推断和预测，为采取正确的决策和行动提供依据和建议。数理统计不同于一般的资料统计，它更侧重于应用随机现象本身的规律性进行资料的收集、整理和分析。

　　【简单的讲】，就是通过样本分析来推断整体。

　　【意义或者重要性】在这个大数据时代，数据是非常重要的。怎样挖掘数据内部的规律或者隐含的信息，变得尤为重要。当时我们是不可能获得整体的数据的，所以我们只能通过抽取样本，进而通过样本来推断整体的规律。

　　【目录】

　　第一章、样本与统计量

　　　　一、引言：

　　　　二、总体与样本：

　　　　三、统计量：

　　　　四、常用分布：

　　第二章、参数估计

　　　　一、引言：

　　　　二、点估计——矩估计法：

　　　　三、点估计——极大似然估计：

　　　　四、估计量的优良性准则

　　　　五、区间估计——正态分布

　　　　　　1、引入

　　　　　　2、单个正态总体参数的区间估计

　　　　　　3、两个正态总体的区间估计

　　　　六、区间估计——非正态分布：

　　　　　　1、大样本正态近似法

　　　　　　2、二项分布

　　　　　　3、泊松分布

　　第三章、假设检验

　　　　一、引言：

　　　　二、正态总体均值的假设检验

　　　　　　1、单正态总体 N(μ, σ²)均值 μ 的检验

　　　　　　　　（1） 双边检验 H₀: μ = μ₀；H₁: μ≠μ₀ 

　　　　　　　　（2） 单边检验 H₀: μ = μ₀；H₁: μ>μ₀

　　　　　　2、两个正态总体 N(μ₁, σ₁²) 和  N(μ₂, σ₂²)均值的比较

　　　　　　　　（1） 双边检验 H₀: μ₁ = μ₂；H₁: μ₁≠μ₂ 

 　　　　　　  　（2） 单边检验 H₀: μ₁ >= μ₂；H₁: μ₁<μ₂ 

　　　　　　　　（3） 单边检验 H₀: μ₁ <= μ₂；H₁: μ₁>μ₂ 

　　　　三、正态总体方差的检验

　　　　　　1、单个正态总体方差的 χ2 检验

　　　　　　　　（1） H₀: σ² =σ₀²；H₁: σ² ≠σ₀²

　　　　　　　　（2） H₀: σ² =σ₀²；H₁: σ² >σ₀²

　　　　　　　　（3)  H₀: σ² ≤σ₀²；H₁: σ² > σ₀² (同2.)

　　　　　　2、两正态总体方差比的 F 检验

　　　　　　　　　(1).  H₀: σ₁² = σ₂²；H₁: σ₁² ≠  σ₂².

　　　　　　　　 （2） H₀: σ₁² = σ₂²；H₁:    σ₁²> σ₂²

　　　　　　　　 （3） H₀: σ₁² ≤ σ₂²；H₁:    σ₁²> σ₂²

第三章、假设检验

　　一、引言：

　　下面，我们讨论不同于参数估计问题的另一类统计推断问题——根据样本提供的信息，检验总体的某个假设是否成立的问题。这类问题称为假设检验。

　　假设检验可分为两类：

　　1、参数检验：总体分布已知情形下，检验未知参数的某个假设。

　　2、非参数检验：总体分布未知情形下的假设检验问题。

　　先看一个例子：

　　【例1】某工厂生产 10 欧姆的电阻，根据以往生产的电阻实际情况，可以认为: 电阻值 X服从正态分布 N(μ, 0.1²)。现在随机抽取10个电阻, 测得它们的电阻值为:9.9, 10.1, 10.2, 9.7, 9.9, 9.9, 10.0, 10.5, 10.1, 10.2.问: 从样本看，能否认为该厂生产的电阻的平均值 μ = 10 欧姆?

　　I.  如何建立检验模型

　　●  确定总体：记 X 为该厂生产电阻的测值，则 ：X ～ N(μ, 0.1²)；

　　●  明确任务：通过样本推断 “X 的均值 μ 是否等于10欧姆”；

　　●  假设：上面的任务是要通过样本检验“X 的均值μ =10”这一假设是否成立。

　　在数理统计中，把 “ X 的均值 μ =10” 这样一个待检验的假设记为 “原假设” 或 “零假设”,记成 “ H₀：μ =10”。

　　原假设的对立面是 “ X  的均值   μ ≠10”，称为  “对立假设” 或 “备择假设”，记成   “ H₁:μ ≠10”。把原假设和对立假设合写在一起，就是:H₀：μ =10； H₁：μ≠10.

　　II.  解决问题的思路

　　　　

　　这里的问题是：如何确定常数 c 呢？细致地分析:根据中心极限定理，有

　　　　

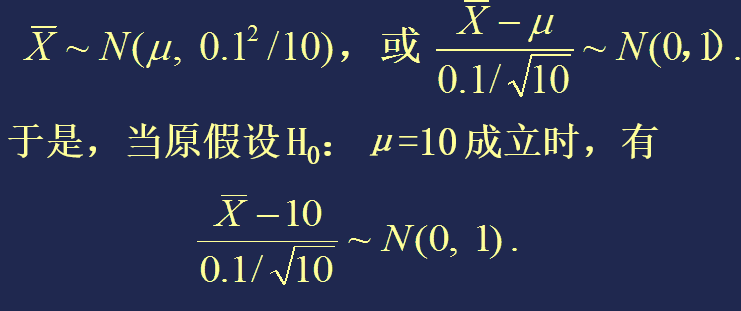
　　为确定常数 c，我们考虑一个很小的正数a， 如a = 0.05。当原假设 H₀: μ =10 成立时，有

　　　　

　　　　

　　　　

　　III.  方法原理：小概率发生（落入拒绝域），则拒绝。

　　　　

　　IV. 两类错误与显著性水平

　　当我们检验一个假设 H₀ 时，有可能犯以下两类错误之一：H₀ 是正确的，但被我们拒绝了，这就犯了“弃真”的错误，即抛弃了正确假设；H₀ 是不正确的，但被我们接受了，这就犯了“取伪”的错误，即采用了伪假设。

      因为检验统计量总是随机的，所以，我们总是以一定的概率犯以上两类错误。

　　通常用 α 和 β  记犯第一、第二类错误的概率，即 

　　α = P{ 拒绝H₀ | H₀ 为真 }

　　β = P{ 接受H₀ | H₀ 为假 }

　　在检验问题中，犯“弃真”和“取伪”两类错误都总是不可避免的，并且减少犯第一类错误的概率，就会增大犯第二类错误的概率;反之亦然。 所以，犯两类错误的概率不能同时得到控制。

　　在统计学中，通常控制犯第一类错误的概概率。一般事先选定一个数 a(0<a<1)，要求犯第一类错误的概率不超过 a。称 a 为假设检验的显著性水平，简称水平。犯第二类错误的概率的计算超出了课程的学习范围。因此，不作讨论。   

　　【例1(续)】分析该例的显著性水平。

　　　　

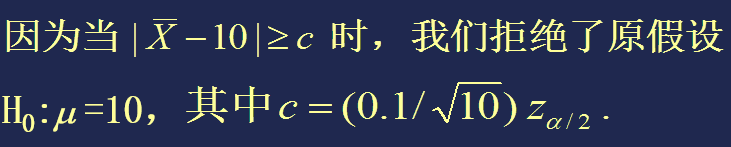
　　现在我们来分析一下：取上述  c  后，如果  H₀ 是正确的，却被我们拒绝了。这时，犯第一类错误的概率是多少呢？

　　　　

二、正态总体均值的假设检验

1、单正态总体 N(μ, σ²)均值 μ 的检验

（1） 双边检验 H₀: μ = μ₀；H₁: μ≠μ₀ 

　　假设 σ²已知，根据上节中的例1，当原假设 H₀:  μ = μ₀ 成立时，有 

　　　　

　　　　

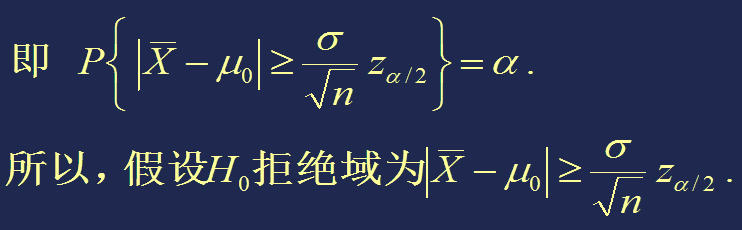
　　以上检验法称作 U 检验法。

　　在应用上，σ²未知的情况是常见的。此时，和前面不同的是：常用样本方差 S²代替未知的σ² 。

　　　　

　　此检验法称作  t  检验法。

　　　　

（2） 单边检验 H₀: μ = μ₀；H₁: μ>μ₀ 

　　上一段中， H₀:μ=μ₀ ;  H₁: μ≠μ₀ 的对立假设为 H₁: μ ≠μ₀ , 该假设称为双边对立假设。而现在要处理的对立假设为 H₁: μ >μ₀,  称为右边对立假设。

 　　类似地，H₀: μ =μ₀; H₁: μ <μ₀ 中的对立假设H₁: μ <μ₀，假设称为左边对立假设。右边对立假设和左边对立假设统称为单边对立假设，其检验为单边检验。

　　例如：工厂生产的某产品的数量指标服从正态分布，均值为 μ₀ ；采用新技术或新配方后，产品质量指标还服从正态分布，但均值为 μ。我们想了解 “μ是否显著地大于μ₀”,即产品的质量指标是否显著地增加了。

　　　　

　　　　

　　【例 2】某厂生产一种工业用绳,其质量指标是绳子所承受的最大拉力，假定该指标服从正态分布，且该厂原来生产的绳子指标均值 μ₀ =15公斤，采用一种新原材料后,厂方称这种原材料提高了绳子的质量，也就是说绳子所承受的最大拉力 μ 比15公斤增大了。

    为检验该厂的结论是否真实，从其新产品中随机抽取50件，测得它们所承受的最大拉力的平均值为15.8公斤，样本标准差S=0.5公斤。取显著性水平a =0.01。问从这些样本看：能否接受厂方的结论。

　　　　

2、两个正态总体 N(μ₁, σ₁²) 和  N(μ₂, σ₂²)均值的比较

　　在应用上，经常会遇到两个正态总体均值的比较问题。

　　例如：比较甲、乙两厂生产的某种产品的质量。将两厂生产的产品的质量指标分别看成正态总体 N(μ₁, σ₁²) 和 N(μ₂, σ₂²)。比较它们的产品质量指标的问题，就变为比较这两个正态总体的均值 μ₁和 μ₂的的问题。

　　又如：考察一项新技术对提高产品质量是否有效。将新技术实施前后生产的产品质量指标分别看成正态总体 N(μ₁, σ₁²) 和 N(μ₂, σ₂²)。这时，所考察的问题就归结为检验这两个正态总体的均值 μ₁和 μ₂是否相等的问题。   

　　　　

　　　　

　　　　

 　　　　

　　　　

【说明】

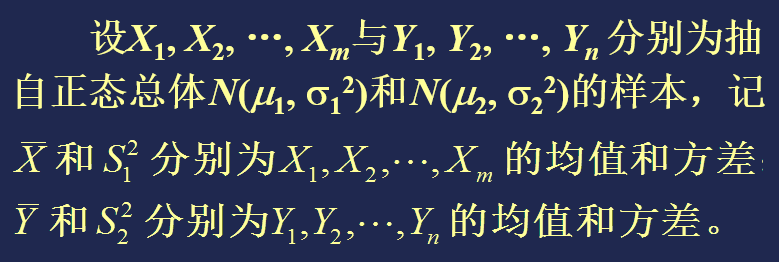
　　上面，我们假定 σ₁²=σ₂²。当然，这是个不得已而强加上去的条件，因为如果不加此条件，就无法使用简单易行的 t 检验。

      在实用中，只要我们有理由认为σ₁²和σ₂²相差不是太大，往往就可使用上述方法。通常是：如果方差比检验未被拒绝(见下节), 就认为σ₁²和σ₂²相差不是太大。

　　【例3】假设有A和B两种药，欲比较它们在服用2小时后在血液中的含量是否一样。对药品A，随机抽取8个病人服药，服药2小时后，测得8个病人血液中药物浓度(用适当的单位)分别为:

     1.23, 1.42, 1.41, 1.62, 1.55, 1.51, 1.60, 1.76.

　　对药品B，随机抽取6个病人服药，服药2小时后，测得血液中药的浓度分别为: 1.76, 1.41,  1.87, 1.49, 1.67, 1.81.

　　假定这两组观测值抽自具有共同方差的两个正态总体，在显著性水a=0.10下，检验病人血液中这两种药的浓度是否有显著不同?

　　　　

　　　　

　　　　

三、正态总体方差的检验

　　1、单个正态总体方差的 χ2 检验

　　设 X₁, X₂, …, X_n 为来自总体 N(μ , σ²) 的样本，μ  和 σ²未知，求下列假设的显著性水平为 a  的检验。

　　（1） H₀: σ² =σ₀²；H₁: σ² ≠σ₀²

　　【思路分析】利用样本方差 S²是 σ²的一个无偏估计，且 (n-1)S²/  σ² ~ χ²_n-1 的结论。

　　当原假设 H₀: σ² = σ₀²成立时，S²和σ₀²应该比较接近，即比值 S²/σ₀²应接近于1。所以,这个比值过大或过小 时，应拒绝原假设。

     合理的做法是:  找两个合适的界限 c₁ 和 c₂ ,

　　● 当 c₁<(n-1)S²/σ₀² < c₂ 时，接受H₀；

　　● 当 (n-1)S²/σ₀²≤c₁ 或 (n-1)S²/σ₀²≥c₂ 时,   拒绝 H₀ 。    

　　　　

　　（2） H₀: σ² =σ₀²；H₁: σ² >σ₀²

　　　　

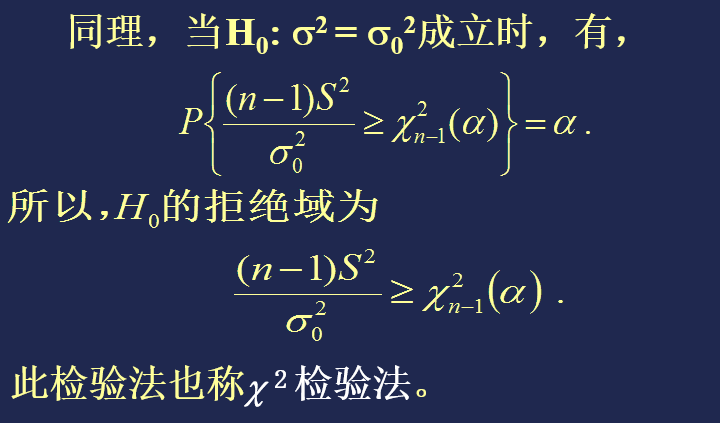
　　（3)  H₀: σ² ≤σ₀²；H₁: σ² > σ₀² (同2.)

 

　　【例1】某公司生产的发动机部件的直径 (单位: cm) 服从正态分布，并称其标准差 σ₀=0.048 。现随机抽取5个部件，测得它们的直径为 1.32, 1.55, 1.36, 1.40, 1.44.

取a=0.05，问:

　　(1). 能否认为该公司生产的发动机部件的直径的标准差确实为σ= σ₀?

　　(2). 能否认为σ ≤ σ₀?

　　解:  (1). 的问题就是检验H₀: σ² =σ₀²；H₁: σ² ≠σ₀². 其中，n=5，a =0.05，σ₀=0.048.

　　　　

　　(2).  的问题是检验H₀: σ² ≤σ₀²；H₁: σ² > σ₀².

　　　　

　　2、两正态总体方差比的 F 检验

　　设X₁, X₂, …, X_m和Y₁, Y₂, …, Y_n 分别为抽自正态总体 N(μ₁ , σ₁²)和 N(μ₂ , σ₂²)的样本,  欲检验

　　(1).  H₀: σ₁² = σ₂²；H₁: σ₁² ≠  σ₂².

　　该检验主要用于上节中实施两样本 t 检验之前，讨论  σ₁² = σ₂² 的假设是否合理。

【思路分析】

　　因两总体 N(μ₁ , σ₁²)和 N(μ₂ , σ₂²)的样本方差S₁²和S₂²分别为σ₁²和σ₂²的无偏估计。所以,直观上讲，S₁²/S₂² 是σ₁²/σ₂² 的一个好的估计。

　　当  H0:  σ₁² = σ₂² 成立时,  σ₁²/σ₂²=1,  作为其估计，S₁²/S₂²也应与 1 相差不大。当该值过分地大或过分地小时，都应拒绝原假设成立。

    合理的思路是：找两个界限c₁和c₂,

　　　　● 当 c₁< S₁²/S₂² < c₂ 时，接受H₀；

　　　　● 当 S₁²/S₂² ≤ c₁, 或 S₁²/S₂² ≥ c₂ 时,  拒绝H₀ 。

　　　　

　　　　

　　（2） H₀: σ₁² = σ₂²；H₁:    σ₁²> σ₂²

　　　　

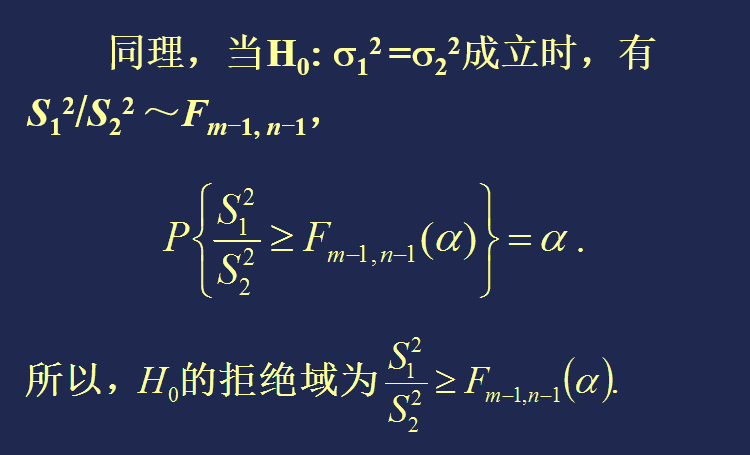
　　（3） H₀: σ₁² ≤ σ₂²；H₁:    σ₁²> σ₂²

　　　　结论同 2。

　　【例2】甲乙两厂生产同一种电阻，现从甲乙两厂的产品中分别随机地抽取12个和10个样品,测得它们的电阻值后，计算出样本方差分别为S₁²=1.40，S₂²=4.38。假设两厂生产的电阻的电阻的阻值分别服从正态分布   N(μ₁ , σ₁²)和 N(μ₂ , σ₂²)。在显著性水平 a = 0.10下, 是否可接受：   (l).σ₁² =σ2²；(2).σ₁²≤σ2².