Counting Stars
http://acm.hdu.edu.cn/showproblem.php?pid=6184
题意:求这样图形的个数。
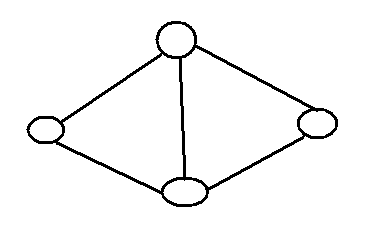
分析:
三元环计数。
两个三元环可以组成一个那样的图形。于是直接枚举一条边,然后求这条边所能构成的三元环。
代码:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<cmath> 5 #include<iostream> 6 #include<cctype> 7 #include<set> 8 #include<vector> 9 #include<queue> 10 #include<map> 11 #define fi(s) freopen(s,"r",stdin); 12 #define fo(s) freopen(s,"w",stdout); 13 using namespace std; 14 typedef long long LL; 15 16 inline int read() { 17 int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1; 18 for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';return x*f; 19 } 20 21 const int N = 100005; 22 23 vector<int>e[N]; 24 set<LL> s; 25 int A[N], B[N], deg[N], Link[N]; 26 bool vis[N]; 27 28 int main() { 29 int n, m; 30 while (~scanf("%d%d",&n, &m)) { 31 int Size = sqrt(m); 32 s.clear(); 33 for (int i = 1; i <= n; ++i) Link[i] = deg[i] = 0, vis[i] = false, e[i].clear(); 34 for (int i = 1; i <= m; ++i) { 35 int u = read(), v = read(); 36 deg[u] ++, deg[v] ++; 37 e[u].push_back(v), e[v].push_back(u); 38 s.insert(1ll * u * n + v), s.insert(1ll * v * n + u); 39 } 40 LL Ans = 0; 41 for (int u = 1; u <= n; ++u) { 42 vis[u] = true; // 如果没有vis,Ans需要/2 43 for (int i = 0; i < e[u].size(); ++i) Link[e[u][i]] = u; 44 for (int i = 0; i < e[u].size(); ++i) { 45 int v = e[u][i], cnt = 0; 46 if (vis[v]) continue; 47 if (deg[v] <= Size) { 48 for (int j = 0; j < e[v].size(); ++j) 49 if (Link[e[v][j]] == u) cnt ++; 50 } 51 else { 52 for (int j = 0; j < e[u].size(); ++j) 53 if (s.find(1ll * e[u][j] * n + v) != s.end()) cnt ++; 54 } 55 Ans += (1ll * cnt * (cnt - 1) / 2); 56 } 57 } 58 printf("%lld ",Ans); 59 } 60 return 0; 61 }