
rt。用(LaTeX)整理了公式。
之前那篇很混乱而且咕咕咕到现在的随笔:st表、树状数组与线段树 笔记与思路整理
一、构成方式
树状数组是一种树状的结构(废话),但是只需要 $ O(n)$ 的空间复杂度。区间查询和单一修改时间复杂度都为 (O(log n)) ,利用差分区间修改也可以达到 (O(log n)) ,但此时不能区间查询。通过维护两个数组可以达到 (O(log n)) 的区间修改与查询。
树状数组是基于一棵二叉树,为便于思想上向数组转化,这里稍微变形:(Excel绘图23333)
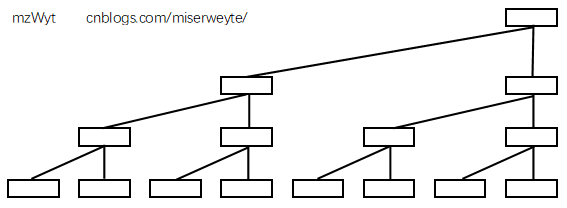
如果要在一棵树上存储一个数组并且便于求和,我们可以想到让每个父节点存储其两个子节点的和。(就决定是你啦!线段树!)
为了达到 (O(n)) 的空间复杂度,删去一些节点(放弃线段树)后如下:
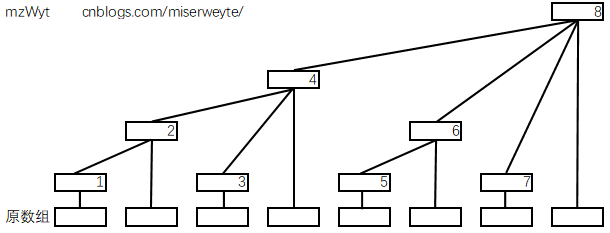
标有序号的节点为树状数组,序号从左向右增大。
二、运算规律
观察上一节的图可得,每个树状数组的节点都储存了(2^k)个原数组节点的数据((k)为节点深度)。也就是说,在上面的图中:
t[1] = a[1];
t[2] = a[1] + a[2];
t[3] = a[3];
t[4] = a[1] + a[2] + a[3] + a[4];
t[5] = a[5];
t[6] = a[5] + a[6];
t[7] = a[7];
t[8] = a[1] + a[2] + a[3] + a[4] + a[5] + a[6] + a[7] + a[8];
所以说,这棵树的(不是我自己推出来的)规律是:
//(k)为(i)的二进制中从最低位到高位连续零的长度
将(2^k)称为(lowbit(i)),则代码如下:
void add(int pos, int val){ //将节点pos增加val
for(int i=pos; i<=n; i+=lowbit(i)){
t[i] += val;
}
}
int ask(int pos){ //求节点pos前缀和
int ans = 0;
for(int i=pos; i>0; i-=lowbit(i)){
ans += t[i];
}
return ans;
}
int query_sum(int l, int r){ //利用前缀和求[l, r]总和
return ask(r) - ask(l);
}
那么问题来了,怎么求这个 (2^k) 呢?
有一个巧妙的(我自己也没推出来的)算法是:
抄一段证明如下:
这里利用的负数的存储特性,负数是以补码存储的,对于整数运算 (x&(-x))有
● 当(x)为(0)时,即 (0 & 0),结果为(0);//因此实际运算的时候如果真的出现了(lowbit(0))会卡死,要从(1)开始存储
●当(x)为奇数时,最后一个比特位为(1),取反加(1)没有进位,故(x)和(-x)除最后一位外前面的位正好相反,按位与结果为(0)。结果为(1)。
●当(x)为偶数,且为(2^m)时,(x)的二进制表示中只有一位是(1)(从右往左的第(m+1)位),其右边有(m)位(0),故(x)取反加(1)后,从右到左第有(m)个(0),第(m+1)位及其左边全是(1)。这样,(x& (-x)) 得到的就是(x)。
●当(x)为偶数,却不为(2^m)的形式时,可以写作(x= y imes (2^k)) 。其中,(y)的最低位为(1)。实际上就是把(x)用一个奇数左移(k)位来表示。这时,(x)的二进制表示最右边有(k)个(0),从右往左第(k+1)位为(1)。当对x取反时,最右边的(k)位(0)变成(1),第(k+1)位变为(0);再加(1),最右边的(k)位就又变成了(0),第(k+1)位因为进位的关系变成了(1)。左边的位因为没有进位,正好和(x)原来对应的位上的值相反。二者按位与,得到:第(k+1)位上为(1),左边右边都为(0)。结果为(2^k)。
总结一下:(x&(-x)),当(x)为(0)时结果为(0);(x)为奇数时,结果为(1);(x)为偶数时,结果为(x)中(2)的最大次方的因子。
三、具体操作
1.区间查询单点修改
如上文所说,使用循环维护一条树上路径即可。
模板题: 洛谷 P3374
查看源码
#include "bits/stdc++.h"
using namespace std;
int a[500010], t[500010];
int n, m;
int lowbit(int x){
return x & (-x);
}
void add(int pos, int val){
for(int i=pos; i<=n; i+=lowbit(i)){
t[i] += val;
}
}
int query_node(int pos){
int ans = 0;
for(int i=pos; i>0; i-=lowbit(i)){
ans += t[i];
}
return ans;
}
int query_range(int l, int r){
return query_node(r) - query_node(l-1);
}
int main(){
cin >> n >> m;
int opt, pos, l, r, num;
for(int i=1; i<=n; i++){
scanf("%d", &a[i]);
add_node(i, a[i]);
}
while(m--){
scanf("%d", &opt);
if(opt == 1){
scanf("%d%d", &pos, &num);
add_node(pos, num);
}
if(opt == 2){
scanf("%d%d", &l, &r);
printf("%d
", query_range(l, r));
}
}
return 0;
}2.单点查询区间修改
利用差分的思想,设数组(b[i]=a[i]-a[i-1]),用树状数组(t[~])表示(b[~])。(这里默认(a[0]=b[0]=0))
来一组样例:
(a[~]={1,~5,~4,~2,~3,~1,~2,~5})
(b[ ] = { 1, 4, -1, -2, 1, -2, 1, 3})
处理区间([1, 5]),将其中所有元素+1:
(a[~]={1,~{color{red}{6,~5,~3,~4,~2,}}~2,~5})
(b[ ] = { 1, {color{red}5,} -1, -2, 1, -2, {color{red}0,} 3 })
可以看到,只有 (b[1]) 和 (b[6]) 发生了变化。(即更改区间([l, r])时的节点(l)与节点(r+1))因此,以 (b[ ]) 为原数组的 (t[ ]) 只需要执行两次 (add()) 即可。但是,在查询 (a[i]) 的时候就需要查询 (b[1...i]) 之和,在 (log n) 时间里只能查询单个节点的值。
模板题:洛谷 P3368
查看源码
#include "bits/stdc++.h"
using namespace std;
int a[500010], t[500010];
int n, m;
int lowbit(int x){
return x & (-x);
}
void add_node(int pos, int val){
for(int i=pos; i<=n; i+=lowbit(i)){
t[i] += val;
}
}
void add_range(int l, int r, int val){
add_node(l, val);
add_node(r+1, -val);
}
int query_node(int pos){
int ans = 0;
for(int i=pos; i>0; i-=lowbit(i)){
ans += t[i];
}
return ans;
}
int main(){
cin >> n >> m;
int opt, pos, l, r, num;
for(int i=1; i<=n; i++){
scanf("%d", &a[i]);
add_node(i, a[i] - a[i-1]);
}
while(m--){
scanf("%d", &opt);
if(opt == 1){
scanf("%d%d%d", &l, &r, &num);
add_range(l, r, num);
}
if(opt == 2){
scanf("%d", &pos);
printf("%d
", query_node(pos));
}
}
return 0;
}3.区间查询区间修改
关于区间查询与区间修改的操作,考虑维护两个树状数组来优化差分:
(本段参考了xenny的博客)
(sum_{i=1}^{n}a[i] =sum_{i=1}^n sum_{j=1}^it[j])
则
所以上式可以变为(∑^n_{i = 1}a[i] = n∑^n_{i = 1}t[i] - ∑^n_{i = 1}( t[i] * (i - 1) ))
因此,实现了区间查询与区间修改之后可以实现线段树的某些功能。但这种实现方式与线段树还有所差异,详情见下一节“优势与局限”。
模板题:洛谷 P3372 (线段树模板1)
查看源码
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
ll a[500010], t1[500010], t2[500010];
int n, m;
int lowbit(int x){
return x & (-x);
}
void add_node(int pos, ll val){
for(int i=pos; i<=n; i+=lowbit(i)){
t1[i] += val;
t2[i] += val * (pos-1);
}
}
void add_range(int l, int r, int val){
add_node(l, val);
add_node(r+1, -val);
}
ll quary_node(int pos){
ll ans = 0;
for(int i=pos; i>0; i-=lowbit(i)){
ans += pos * t1[i] - t2[i];
}
return ans;
}
ll quary_range(int l, int r){
return quary_node(r) - quary_node(l-1);
}
int main(){
cin >> n >> m;
int opt, pos, l, r;
ll num;
for(int i=1; i<=n; i++){
scanf("%d", &a[i]);
add_node(i, a[i] - a[i-1]);
}
while(m--){
scanf("%d", &opt);
if(opt == 1){
scanf("%d%d%lld", &l, &r, &num);
add_range(l, r, num);
}
if(opt == 2){
scanf("%d %d", &l, &r);
printf("%lld
", quary_range(l, r));
}
}
return 0;
}四、优势与局限
很显然,在相同的实现下(区间查询、区间修改),树状数组的码量要小于线段树等,运行时的常数与占用空间也较小。
但实际上,树状数组只能维护前缀操作和(前缀和,前缀积,前缀最大最小),而线段树可以维护区间操作和。
使用树状数组来“维护区间操作和”的实现,本质上是取右端点的前缀和,然后对左端点左边的前缀和的逆元做一次操作。因此,如果不存在逆元的操作(乘法(P.s.:模不为质数)、区间最值等)就无法用树状数组完成。