所谓的二分图,就是指图中的所有顶点可以分为两个集合A和B,并且图中的每条边的两个顶点都是一个在A,一个在B,则该图是一个二分图。
下面我们来解释几个关于二分图的一些相关概念。
(1)最大匹配
在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题,最大匹配的边数称为最大匹配数.如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
(2)最优匹配
最优匹配又称为带权最大匹配,是指在带有权值边的二分图中,求一个匹配使得匹配边上的权值和最大。一般A和B集合顶点个数相同,最优匹配也是一个完备匹配,即每个顶点都被匹配。如果个数不相等,可以通过补点加0边实现转化。一般使用KM算法解决该问题。
(3)最小覆盖
二分图的最小覆盖分为最小顶点覆盖和最小路径覆盖:
①最小顶点覆盖是指最少的顶点数使得二分图G中的每条边都至少与其中一个点相关联,二分图的最小顶点覆盖数=二分图的最大匹配数;
②最小路径覆盖也称为最小边覆盖,是指用尽量少的不相交简单路径覆盖二分图中的所有顶点。二分图的最小路径覆盖数=|V|-二分图的最大匹配数;
(4)最大独立集
最大独立集是指寻找一个点集,使得其中任意两点在图中无对应边。对于一般图来说,最大独立集是一个NP完全问题,对于二分图来说最大独立集=|V|-二分图的最大匹配数。如下图中黑色点即为一个最大独立集:
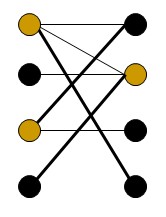
我们可以看到二分图的一些性质。
(1)二分图中的所有回路的边数都是偶数。
(2)二分图的独立数等于顶点数减去最大匹配数
(3)DAG的最小路径覆盖,将每个点拆点后作最大匹配,结果为n-m,求具体路径的时候顺着匹配边走就可以,匹配边i→j',j→k',k→l'....构成一条有向路径。
(4)最大匹配数=左边匹配点+右边未匹配点。因为在最大匹配集中的任意一条边,如果他的左边没标记,右边被标记了,那么我们就可找到一条新的增广路,所以每一条边都至少被一个点覆盖。
(5)最小边覆盖=图中点的个数-最大匹配数=最大独立集。
关于二分图求最大匹配(匈牙利算法)详见https://blog.csdn.net/thundermrbird/article/details/52231639