算法分析
Introduction
有各种原因要求我们分析算法,像预测算法性能,比较不同算法优劣等,其中很实际的一条原因是为了避免性能错误,要对自己算法的性能有个概念。
科学方法(scientific method)也适用于算法分析,它提供了一个预测性能和比较算法的框架:
- Observe 观察真实世界的某些特征
- Hypothesize 根据观察结果提出假设模型
- Predict 用模型预测未来的事件
- Verify 继续观察来核实预测的准确性
- Validate 重复直到预测和观察一致
此外还有两条原则:
- reproduceible 实验得是别人可以重现的
- falsifiable 假设可以被实验证伪
Observations
先给出一个例子,叫 3-sum 问题,即给定一组数,问三数之和为零的有哪些组合,据说在计算几何中很有用。暴力求解的算法很简单,三个 for 循环。
3-Sum Brute-Force Algorithm
public class ThreeSum {
public static int count(int[] a) {
int N = a.length;
int count = 0;
for (int i = 0; i < N; i++)
for (int j = i + 1; j < N; j++)
for (int k = j + 1; k < N; k++)
if (a[i] + a[j] + a[k] == 0)
count++;
return count;
}
public static void main(String[] args) {
int[] a = In.readInts(args[0]);
StdOut.println(count(a));
}
}
分析算法时的观测即是看程序的运行时间,你可以用秒表计时,或是使用 java 中计时的类。
public static void main(String[] args) {
int[] a = In.readInts(args[0]);
Stopwatch stopwatch = new Stopwatch();
StdOut.println(ThreeSum.conut(a));
double time = stopwatch.elapsedTime();
}
运行这个程序,就可以知道上述暴力算法的运行时间。

有了这些数据,我们可以画出运行时间和输入数据规模 N 的函数图像。
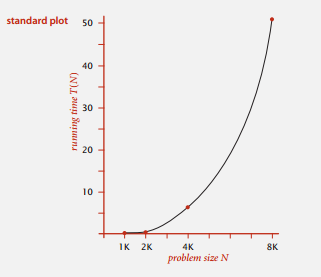
这个不好求二者关系,我们还可以画成双对数的形式。
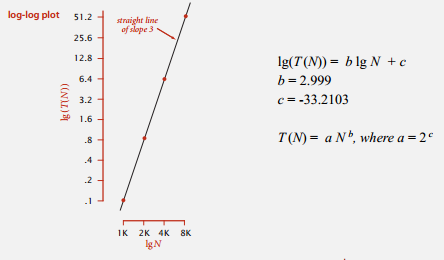
这张图看起来好求些,但其实我们都不用画图。
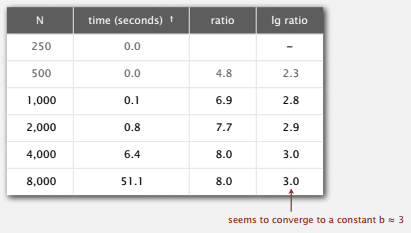
每次运行将数据规模翻倍,由式子 (aN^{b}) ,前后运行时间之比即为 (2^{b}) ,再取 (lg) ,就可大致知道 b 的级别。知道 b 再随便带入一点计算,即可得到 a 。求出 a 和 b 就可以用输入数据规模 N 来预测运行时间了。
b 由算法和输入数据决定,a 则还会受到软硬件等各方面的影响,所以我们很难得到准确的测量。但比起其他科学,我们的实验成本很低,可以进行大量的实验。
Mathematical Models
原则上我们仍然可能构造出一个数学模型来描述任意程序的运行时间,总运行时间即为每个操作的耗时和频率乘积的总和。耗时和计算机硬件,Java 编译器,操作系统等有关,后者则取决于算法和输入。
但我们不是理论家,不需要这么精确,可以简化计算,粗略的估计依然很有用。
Simplification 1: Cost Model
成本模型,用开销最大的或执行次数最多的基本操作来估计运行时间,这里选取访问数组这个操作。

Simplification 2: Tilde Notation
忽略式子中的低阶项,当 N 很大的时候,低阶项并没有什么影响,N 很小时的情况我们并不关心。

f(N)~g(N) 代表着 (limlimits_{x ightarrow 0} frac{f(N)}{g(N)}) (附:LaTeX)。
Order-of-Growth Classifications
增长数量级的分类,我们在实现算法时使用了几种结构性的原语,像循环,嵌套语句,所以成本增长的数量级一般都是问题规模 N 的若干函数之一。
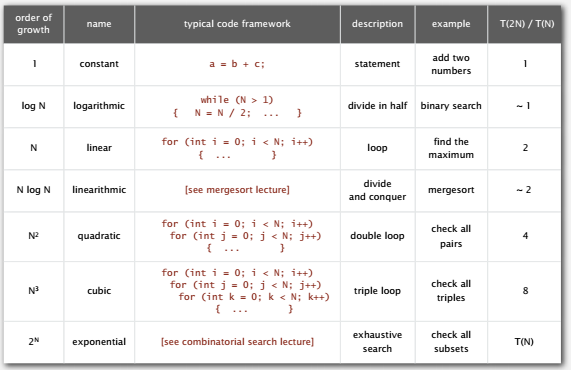
从双对数图更能说明平方级别和立方级别的算法对于大规模的问题是不可用的。

因此,我们自然希望为各种基础问题找到对数级别、线性级别或是线性对数级别的算法。
上面提到的 3-Sum 问题,暴力求解是立方级别,我们可以用二分查找对其做些改进。
Binary Search
public static int binarySearch(int[] a, int key) {
int lo = 0, hi = a.length-1;
while (lo <= hi) {
int mid = lo + (hi - lo) / 2;
if (key < a[mid]) hi = mid - 1;
else if (key > a[mid]) lo = mid + 1;
else return mid;
}
return -1;
}
二分查找在大小为 N 的有序数组中最多只要进行 (1 + lgN) 次比较,也就是对数级别。
可以递推地证明这一结论。

于是我们第一步要对数组进行排序,随便来个平方级别的插入排序,然后对数组中每一对 a[i] 和 a[j] ,二分查找 -(a[i] + a[j]) ,这是 (N^{2}logN) 级别,总的来说这算法是 (N^{2}logN) 级别的。
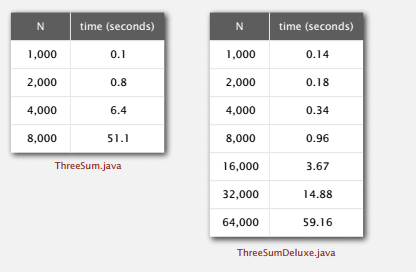
可以看出这样也比原来立方的级别好很多,更好的数量级,更好的性能表现。
Theory of Algorithms
而实际情况会比上面的例子复杂些,事实是对不同的输入,算法会有不同的性能表现。像二分查找,其实最好的情况是常数级别的。所以针对不同的输入,我们经常需要从不同的角度来分析问题,可分为最好、最差和平均三种类型。但实际的数据不会简单的就是这三种情况,更一般地做法是我们按最坏情况设计算法或是考虑随机情况下某种概率的性能保证。
在算法理论中,我们想要知道问题有多困难,解决它的最佳算法是什么。在分析中,我们希望去掉尽可能多的细节,将分析做到只差一个常数倍数的精度,增长阶数分析可以做到。我们还想做到不用考虑输入情况,所以将重点放在针对最坏情况的算法设计,然后就可以只用增长阶数来讨论算法性能。
为了描述性能的界限,有一些常用的记号。
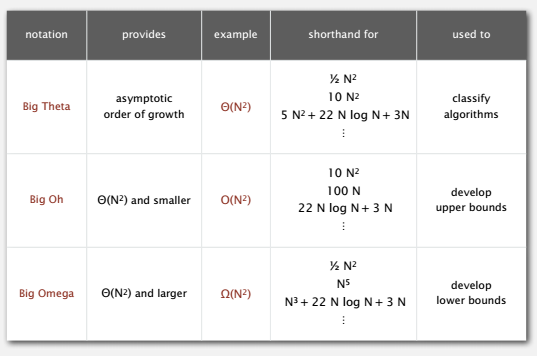
举例来说,1-Sum 问题要找到数组中零元素的个数,我们想要知道问题的难度和最佳算法。暴力求解需要检查数组的每个元素,运行时间是 (O(N)),这为最佳算法提供了一个上界。而其实为了确定数组里有几个零也必须检查数组的每个空,所以解决这个问题的最佳算法的下界也很好确定为 (Omega(N))。除去常数,上下界吻合,暴力算法就是 1-Sum 的最佳算法,运行时间为 (Theta(N))。对于这个简单的问题,找到最佳算法很简单。
对于更复杂的问题,确定上下界就更困难,更别说找到吻合的上下界了。再举例来看3-Sum问题,暴力算法的运行时间是 (O(N^{3})),用二分查找改进的算法则是 (O(N^{2}logN)),这是一个更好的上界。下界按上一个例子的想法可以为 (Omega(N))。上下界之间存在间隔,我们就不知道求解 3-Sum 问题的难度,也不知道最优算法是什么,这是个开放问题。我们寻找新的能够降低上界的算法或者寻找提高下界的方法,以此来了解问题的计算难度,找到最佳算法,这是一个富有魅力的研究领域,很多问题上下界之间仍有间隔。
但关注最坏情况对我们来说可能有些过于悲观,还是留给算法理论学家们吧。而且真的要预测性能和比较算法时,需要比常数因子级误差更准确的分析。所以我们讲了波浪(~)记号,以及在算法理论中使用的常用记号。需要注意的是,很多人错把 (O) 分析的结果当作运行时间的近似模型,其实应该是问题更好的上界,这门课中,我们使用波浪记号来表示近似模型。
Memory
内存的使用和具体的机器实现相关,我们用 典型 这个词暗示和机器相关的值。
典型的 Java 实现用 1 字节表示一个 boolean 值,因为计算机访问内存的方式都是一次 1 字节。同时,我们假设表示机器地址需要 8 字节,这是现在广泛使用的 64 位架构中典型表示方式,许多老式的 32 位架构只使用 4 字节表示机器地址。
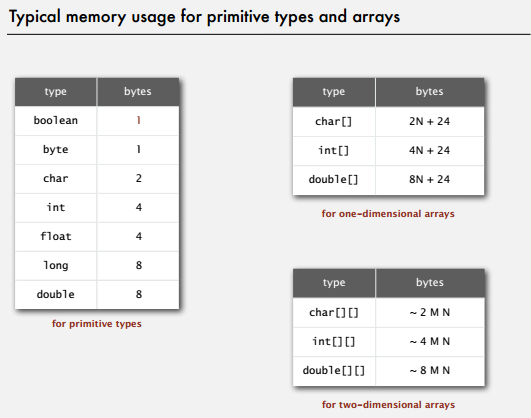
要知道一个对象所使用的内存量,需要将所有实例变量使用的内存与对象本身的开销(一般是 16 字节)相加。这些开销包括一个指向对象的类的引用、垃圾收集信息以及同步信息。另外,一般内存的使用都会被填充为 8 字节( 64 位计算机中的机器字)的倍数。
Java 中数组被实现为对象,它们一般都会因为记录长度而需要额外的内存。一个原始数据类型的数组一般需要 24 字节的头信息( 16 字节的对象开销, 4 字节用于保存长度以及 4 填充字节)再加上保存值所需的内存。
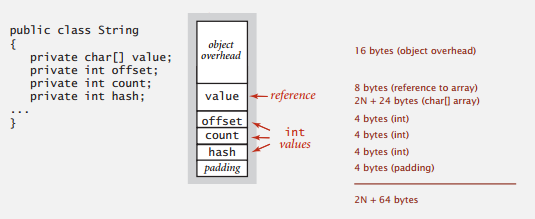
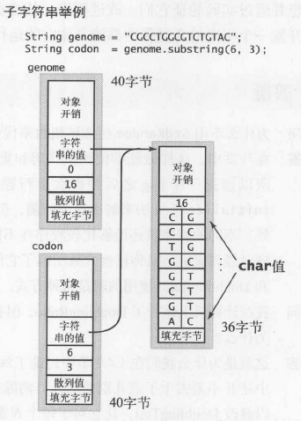
String 的标准实现含有 4 个实例变量:一个指向字符数组的引用( 8 字节)和三个 int 值(各 4 字节)。第一个 int 值描述的是字符数组中的偏移量,第二个 int 值是一个计数器(字符串的长度),这个 String 对象所表示的字符串由 value[offset] 到 value[offset + count - 1] 中的字符组成。String 对象中的第三个 int 值是一个散列值,表示这个对象的哈希码。
字符串处理经常会和子字符串打交道,所以 Java 对字符串的表示希望能够避免复制字符串中的字符。当你调用 substring() 方法时,就创建了一个新的 String 对象( 40 字节),但它仍然重用了相同的 value[] 数组,因此该字符串只会使用 40 字节的内存。含有原始字符串的字符数组的别名存在于子字符串中,子字符串对象的偏移量和长度域标记了子字符串的位置。换句话说,一个子字符串所需的额外内存是一个常数,构造一个子字符串所需时间也是常数,即使字符串和子字符串的长度极大也是这样。
这些基础机制能够有效帮助我们估计大量程序对内存的使用情况,但许多复杂的因素仍然会是这个任务变得更加困难。当涉及函数调用时,内存的消耗就变成了一个复杂的动态过程,这种动态过程使准确估计一个程序内存使用变得极为困难。