Symbol Table Applications

符号表应用

在计算机发展的早期，符号表帮助程序员从使用机器语言的数字地址进化到在汇编语言中使用符号名称；在现代应用程序中，符号名称的含义能够通行于跨域全球的计算机网络。快速查找算法曾经并继续在计算机领域中扮演着重要角色。符号表的现代应用包括科学数据的组织，例如在基因组数据中寻找分子标记或模式从而绘制全基因组图谱；网络信息的组织，从搜索在线贸易到数字图书馆；以及物联网基础架构的实现，例如包在网络节点中的路由、共享文件系统和流媒体等。高效的查找算法确保了这些以及无数其他重要的应用程序成为可能。在本节中我们会考察几个有代表性的例子。

sets

某些符号表的用例不需要处理值，它们只需要能够将键插入表中并检测一个键在表中是否存在。因为我们不允许重复的键，这些操作对应着下面这组 API，它们只处理表中所有键的集合，和相应的值无关。

只要忽略键关联的值或者使用一个简单的类进行封装，你就可以将任何符号表的实现变成一个 SET 类的实现。为了演示 SET 的使用方法，我们来看一组过滤器（filter）实现，它会从标准输入读取一组字符串并将其中一些写入标准输出。经典应用是用一个文件中保存的键来判定输入流中的哪些键可以被传递到输出流。

public class WhiteFilter {
    public static void main(String[] args) {
        HashSET<String> set;
        set = new HashSET<String>();
        In in = new In(args[0]);
        while (!in.isEmpty())
            set.add(in.readString());
        while (!StdIn.isEmpty()) {
            String word = StdIn.readString();
            if (set.contains(word))
                StdOut.println(word);
        }
    }
}

上面是白名单过滤器，输出的 if 语句判断里加个 ! 就可以变成黑名单过滤器。

dictionary clients

符号表使用最简单的情况就是用连续的 put() 操作构造一张符号表以备 get() 查询。许多应用程序都将符号表看做一个可以方便地查询并更新其中信息的动态字典。作为一个具体的例子，我们来看看一个从文件或者网页中提取由逗号分隔的信息（.csv 文件格式）的程序。这种格式存储的列表的信息不需要任何专用的程序就可以读取：数据都是文本，每行中各项均由逗号隔开。

public class LookupCSV {
    public static void main(String[] args) {
        In in = new In(args[0]);
        int keyField = Integer.parseInt(args[1]);
        int valField = Integer.parseInt(args[2]);
        ST<String, String> st = new ST<String, String>();
        while (in.hasNextLine()) {
            String line = in.readLine();
            String[] tokens = line.split(",");
            String key = tokens[keyField];
            String val = tokens[valField];
            st.put(key, val);
        }

        while (!StdIn.isEmpty()) {
            String query = StdIn.readString();
            if (st.contains(query))
                StdOut.println(st.get(query));
        }
    }
}

indexing clients

字典的主要特点是每个键都有一个与之关联的值，因此基于关联型抽象数组来为一个键指定一个值的符号表数据类型正合适。但一般来说，一个给定的键当然有可能和多个值相关联，我们使用索引来描述一个键和多个值相关联的符号表。

下面的 FileIndex 从命令行接受多个文件名，将任意文件中的任意一个单词和一个出现过这个单词的所有文件的文件名构成的 SET 对象关联起来。在接受标准输入的查询时，输出单词对应的文件列表。

import java.io.file;
public class FileIndex {
    public static void main(String[] args) {
        ST<String, SET<File>> st = new ST<String, SET<File>>();
        for (String filename : args) {
            File file = new File(filename);
            In in = new In(file);
            while (!in.isEmpty()) {
                String word = in.readString();
                if (!st.contains(word))
                    st.put(word, new SET<File>());
                SET<File> set = st.get(word);
                set.add(file);
            }
        }

        while (!StdIn.isEmpty()) {
            String query = StdIn.readString();
            if (st.contains(query))
                for (File file : st.get(query))
                    StdOut.println(" " + file.getName());
        }
    }
}

sparse vectors

下面这个例子展示的是符号表在科学和数学计算领域所起到的重要作用。我们要考察的简单计算就是矩阵和向量的乘法：给定一个矩阵和一个向量并计算结果向量，其中第 i 项的值为矩阵的第 i 行和给定的向量的点乘。为了简化问题，我们只考虑 N 行 N 列的方阵，向量的大小也为 N。在 Java 中，用代码实现这种操作非常简单，但所需的时间和 (N^{2}) 成正比，因为 N 维结果向量中每一项都需要计算 N 次乘法。因为需要存储整个矩阵，计算所需的空间也和 (N^{2}) 成正比。

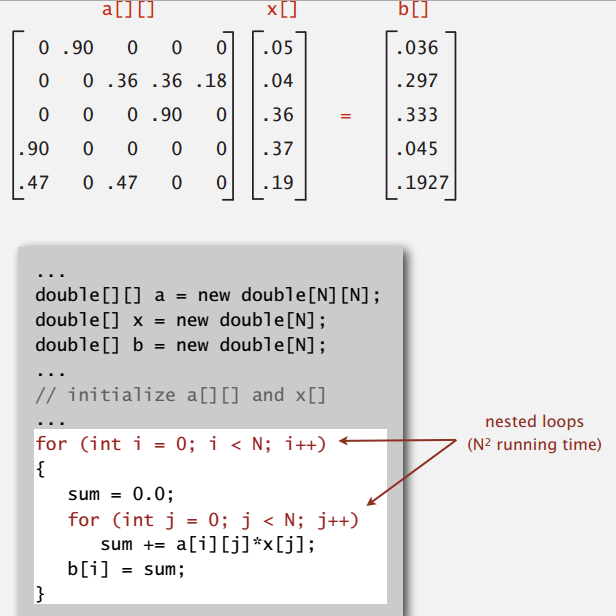
但是在实际应用中，N 往往非常大，而且很多项都是 0，即所谓稀疏矩阵。我们可以将这个矩阵表示为由稀疏向量组成的一个数组，而稀疏向量可以用符号表来高效的表示。

public class SparseVector {
    private HashST<Integer, Double> st;
    public SparseVector() {
        st = new HashST<Integer, Double>();
    }
    public int size() {
        return st.size();
    }
    public void put(int i, double x) {
        st.put(i, x);
    }
    public double get(int i) {
        if (!st.contains(i)) return 0.0;
        else return st.get(i);
    }
    public double dot(double[] that) {
        double sum = 0.0;
        for (int i : st.keys())
            sum += that[i] *this.get(i);
        return sum;
    }
}

稀疏向量的符号表表示中只保存非零项的索引和值，能更高效地完成点乘操作，需要的存储空间也更少。

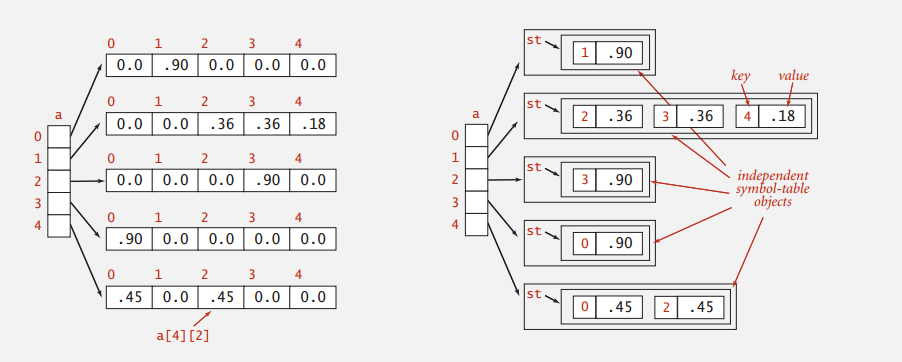
虽然对于较小或是不那么稀疏的矩阵，使用符号表的代价可能会非常高昂但你应该理解它对于巨型稀疏矩阵的意义。