OpenCV学习(5) Mat的基本操作(2)

      本章我们学习一下Mat中的常用操作，因为在后面其它的教程中，我们经常要对图像进行各种处理，也要使用这些操作。

一、 Mat的复制，就是从一个矩阵A，生成相关的另一个矩阵B。

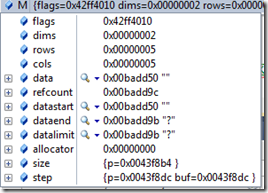
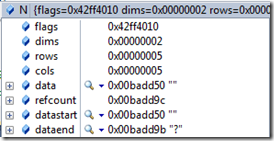
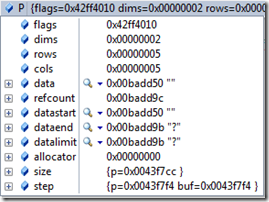
(1)使用赋值的方法，比如通过构造函数生成矩阵N，通过复制生成矩阵P

cv::Mat N(M);
cv::Mat P;
P=M;

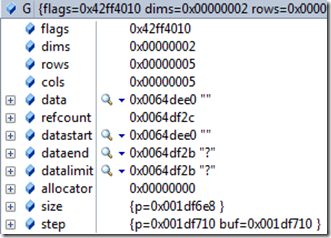
     这样生成的矩阵，只是新生成一个矩阵头，它的data依然指向矩阵M的data，类似C++中的浅拷贝，比如矩阵M，N，P它们的data都指向地址0x00badd50

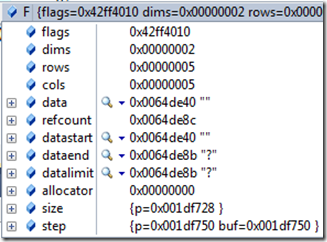
(2) 使用copyTo和clone函数

cv::Mat F = M.clone();
cv::Mat G;
F.copyTo(G);

      这样可以生成一个全新的矩阵，不但复制矩阵的头信息，而且会生成一个data的拷贝。比如矩阵F和M，它们的data指针地址和F是不同的。

      注意：copyTo函数，它还可以带有掩码矩阵copyTo(G, maskImage), maskImage是一个单通道的矩阵，值为0的位置，在拷贝时候并不会拷贝。

二、Mat中常用的几个函数

1. convertTo(OutputArray m, int rtype, double alpha=1, double beta=0 )

生成一个新矩阵，矩阵的中值为原矩阵中的值乘以alpha，然后再加上beta

imageMask.convertTo(mark1,CV_8U);

2. Mat::reshape(int cn)，改变矩阵的维数，比如把二维矩阵改变成一维矩阵。这个操作只是改变矩阵的头信息，比如在没有padding数据情况下，便于数据处理，有时候我们会把二维矩阵变成一维矩阵。

imageMask.reshape(1)；

3. isContinous，检测矩阵是否有padding数据。

double sum=0;
int cols = M.cols, rows = M.rows;
if(M.isContinuous())
{
    cols *= rows;
    rows = 1;
}
for(int i = 0; i < rows; i++)
{
    const double* Mi = M.ptr<double>(i);
    for(int j = 0; j < cols; j++)
        sum += std::max(Mi[j], 0.0);
}

4. 用下面的代码，可以取出矩阵的某个ROI区域，以便进行处理。

cv::Rect rect(100, 100, 100, 100); 

srcImage(rect).copyTo(roiImage); 

5.下面的代码，实现一个矩阵的子矩阵赋值，矩阵roi的data指针会指向result1的data的50行，70列处。

cv::Mat result1= cv::Mat(image1.rows, image1.cols,CV_8UC1, cv::Scalar(cv::GC_BGD));
//注意给子矩阵赋值的方法
cv::Mat roi(result1, cv::Rect(50,70,result1.cols-150,result.rows-180));
roi = cv::Scalar(cv::GC_PR_FGD);

三、简单的三维矩阵示例

//创建一个3维矩阵，每维都是长度为2
int sz[3] = {3,3,3};
cv::Mat L(3,sz, CV_8UC(1), cv::Scalar::all(1));

//打印多维数组
for(i=0; i< 3; i++)
    {
    for(j=0; j<3; j++)
        {
          for(k=0; k<3; k++)
              {
               // printf("%d ", L.data[i*3*3 + j*3 +k]);
              }
        }
    }

四、稀疏矩阵

      有时候，我们需要使用多维矩阵存储一些值，比如三维BGR图像的直方图，由于每维的索引数都是256，所以矩阵元素数量达到256*256*256，如果用普通矩阵存储，需要分配很大的空间，这时候，最好使用稀疏矩阵sparseMat，因为在稀疏矩阵中只保存非零的值。

下面是使用稀疏矩阵的简单例子：

//稀疏矩阵的操作
//创建一个三维的稀疏矩阵
const int dims = 3;
int size[] = {256, 256, 256};
SparseMat sparse_mat(dims, size, CV_32F);
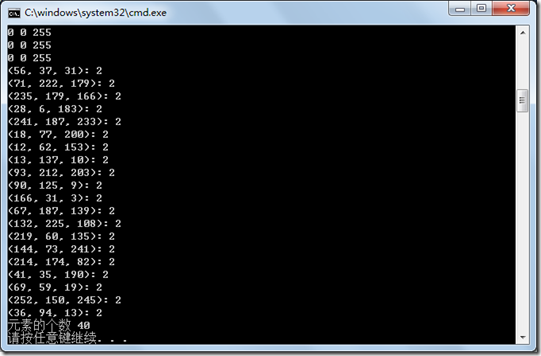
//20个非0的值，注意：稀疏矩阵保存非零的值
for(int i = 0; i < 20; i++)
    {
    int idx[dims];
    for(int k = 0; k < dims; k++)
        idx[k] = rand()%256;
    sparse_mat.ref<float>(idx) = 2.f;
    }

//显示稀疏矩阵的结果
SparseMatConstIterator_<float> it1 = sparse_mat.begin<float>(),    it_end = sparse_mat.end<float>();
double s = 0;
int dims1 = sparse_mat.dims();
for(; it1 != it_end; ++it1)
    {
    // 打印索引和元素的值
    const SparseMat::Node* n = it1.node();
    printf("(");
    for(int i = 0; i < dims1; i++)
        printf("%d%s", n->idx[i], i < dims-1 ? ", " : ")");
    printf(": %g ", it1.value<float>());
    s += *it1;
    }
printf("元素的个数 %g ", s);

程序运行的结果：

源文件：工程FirstOpenCV2。