两个一位的二进制数x,y相加,假设和为s,进位为cout,其真值表为:
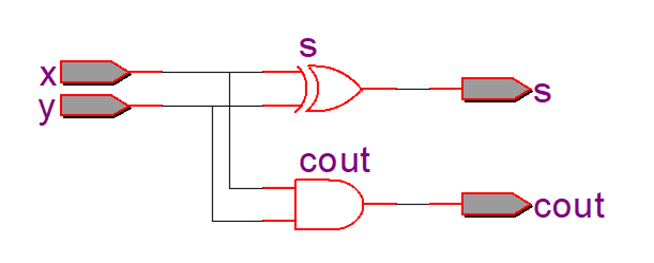
从真值表中,我们可以得到:s = x^y, cout = x&y,实现两个一位数相加的逻辑电路称为半加器。
实现该电路的verilog代码如下:

module halfadd(x,y,s,cout); input x; input y; output s; output cout; assign s = x^y; assign cout = x&y; endmodule
相对应的testbench文件如下代码。在代码中,我们采用系统函数$random来产生随机激励。半加器电路中并没有使用时钟,但在testbench中,产生了时钟信号,主要是为了功能验证时候,有一个时间单位信号,便于检查结果。

`timescale 1ns/1ns
`define clock_period 20
module halfadd_tb;
reg x,y;
wire cout;
wire s;
reg clk;
halfadd halfadd_0(
.x(x),
.y(y),
.s(s),
.cout(cout)
);
initial clk = 0;
always #(`clock_period/2) clk = ~clk;
initial begin
x = 0;
repeat(20)
#(`clock_period) x = $random;
end
initial begin
y = 0;
repeat(20)
#(`clock_period) y = $random;
end
initial begin
#(`clock_period*20)
$stop;
end
endmodule
在quartus II中,分析与综合后,用rtl view 可以得到 halfadd的电路如下,和我们预想的一样。
功能仿真结果如下,从波形中可以看到结果正确。
全编译后,在Cyclone IV E-EP4CE10F17C8中的门级仿真结果如下,输入和输出之间,会有几ns的时延。
通常,我们更感兴趣的是多位二进制数的相加,在多位二进制数相加时,对每一位而言,除了考虑相加的两位数(第i位),还要考虑来自低位(i-1位)的进位。实现带低位进位的两个一位数相加的逻辑电路,称为全加器。
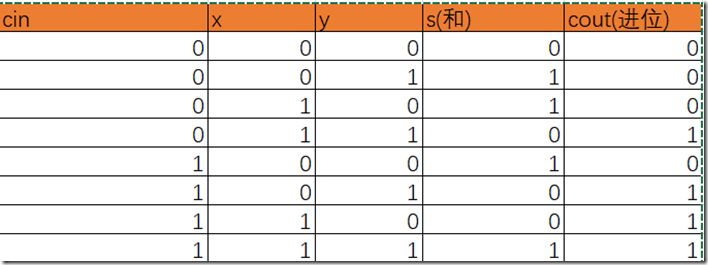
它的真值表如下:
从真值表中,我们可以得知:s = ~x & y & ~cin + x&~y&~cin+~x&~y&cin+x&y&cin = (~x&y+x&~y)&~cin+(~x&~y+x&y)&cin=(x^y)&~cin+~(x^y)&cin=x^y^cin,
这儿我们用~表示非,+表示或。cout = x&y+x&cin+y&cin
全加器verilog代码如下:

module fulladd(cin,x,y,s,cout); input cin; input x; input y; output s; output cout; assign s = x^y^cin; assign cout = (x&y)|(x&cin)|(y&cin); endmodule
对应的testbench代码如下:

`timescale 1ns/1ns
`define clock_period 20
module fulladd_tb;
reg cin,x,y;
wire cout;
wire s;
reg clk;
fulladd fulladd_0(
.cin(cin),
.x(x),
.y(y),
.s(s),
.cout(cout)
);
initial clk = 0;
always #(`clock_period/2) clk = ~clk;
initial begin
x = 0;
repeat(20)
#(`clock_period) x = $random;
end
initial begin
y = 0;
repeat(20)
#(`clock_period) y = $random;
end
initial begin
cin = 0;
repeat(2)
#(`clock_period*10) cin = {$random};
end
initial begin
#(`clock_period*20)
$stop;
end
endmodule
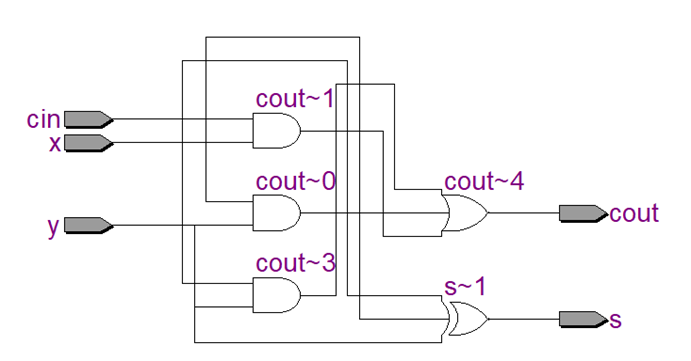
从rtl view中,可以看到全加器逻辑电路图如下:包括3个与门,一个三输入的异或门,一个三输入的或门。
功能仿真和门级仿真的波形如下,信号符合预期。