1.引言
k近邻法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一种基本分类与回归方法。KNN 模型可以获得精确的推荐结果并为结果给出合理的解释,它们是CF 推荐系统中最早被使用也是直至目前最流行的一类模型。
2.KNN算法模型
2.1算法模型图示
它的工作原理是:
存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。

2.2KNN算法思想
在训练集中数据和标签已知的情况下,输入测试数据,将测试数据的特征与训练集中对应的特征进行相互比较,
找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类,
其算法的描述为:
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。
2.3算法实现步骤
为了获得用户对产品的评分预测值,kNN 模型一般包括以下三步:
1. 计算相似度
这步中计算每对产品之间的相似度(similarity)。一些被广泛使用的相似度
测度包括:
欧氏距离:

n:电影分类中的n个特征
p,q:两个样本点
Pearson correlation:


为了预测用户u 对电影m 的评分值,我们首先从Pu 中选取与电影m有最高相似度的特定数量的电影,这些电影形成u−m 对的邻居(neighborhood),记为N(m; u) 。
3. 产生预测值
用户u 对电影m 的评分预测为上步获得的邻居N(m; u) 中评分的加权平均值:


3.实例测试
k-近邻算法的一般流程:
收集数据:可以使用爬虫进行数据的收集,也可以使用第三方提供的免费或收费的数据。一般来讲,数据放在txt文本文件中,按照一定的格式进行存储,便于解析及处理。
准备数据:使用Python解析、预处理数据。
分析数据:可以使用很多方法对数据进行分析,例如使用Matplotlib将数据可视化。
测试算法:计算错误率。
使用算法:错误率在可接受范围内,就可以运行k-近邻算法进行分类。
##3.1 实战背景
海伦女士一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的任选,但她并不是喜欢每一个人。经过一番总结,她发现自己交往过的人可以进行如下分类:
(1)不喜欢的人
(2)魅力一般的人
(3)极具魅力的人
海伦收集约会数据已经有了一段时间,她把这些数据存放在文本文件datingTestSet.txt中,每个样本数据占据一行,总共有1000行。
海伦收集的样本数据主要包含以下3种特征:
每年获得的飞行常客里程数
玩视频游戏所消耗时间百分比
每周消费的冰淇淋公升数
##3.2 准备数据:数据解析
在将上述特征数据输入到分类器前,必须将待处理的数据的格式改变为分类器可以接收的格式。要将数据分类两部分,即特征矩阵和对应的分类标签向量。
数据解析结果如图:

可以看到,我们已经顺利导入数据,并对数据进行解析,格式化为分类器需要的数据格式。接着我们需要了解数据的真正含义。可以通过友好、直观的图形化的方式观察数据。
##3.3 分析数据:数据可视化
可视化结果如图:
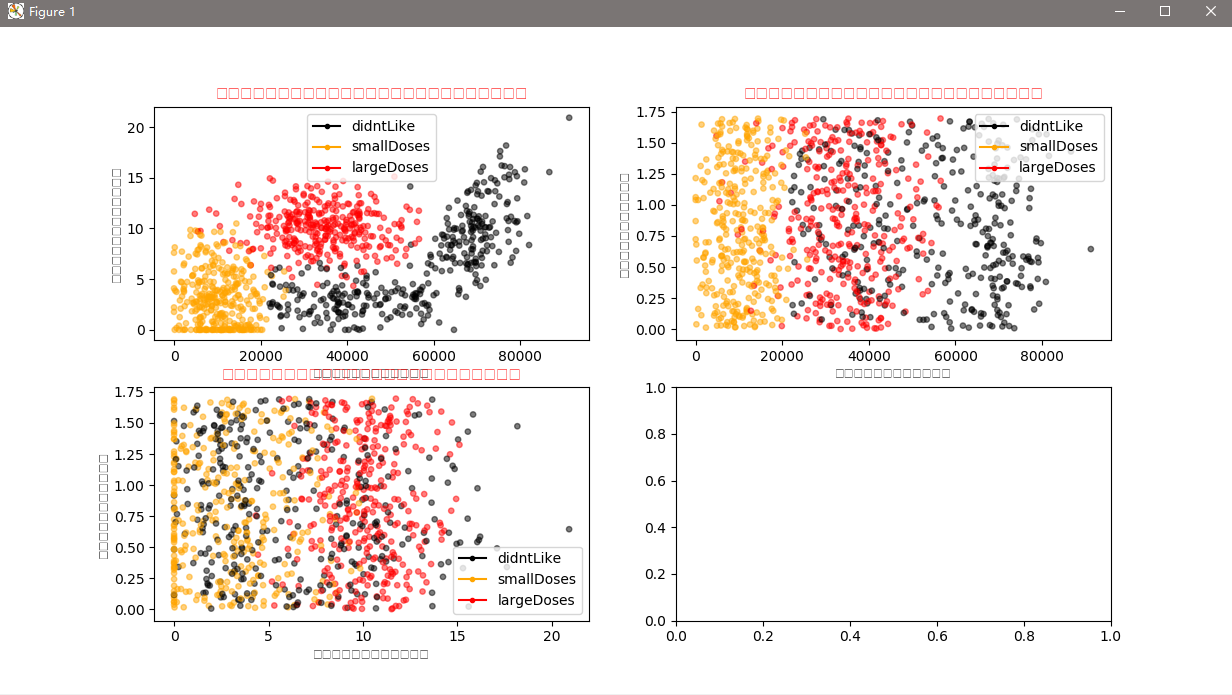
通过数据可以很直观的发现数据的规律,比如以玩游戏所消耗时间占比与每年获得的飞行常客里程数,只考虑这二维的特征信息,给我的感觉就是海伦喜欢有生活质量的男人。为什么这么说呢?每年获得的飞行常客里程数表明,海伦喜欢能享受飞行常客奖励计划的男人,但是不能经常坐飞机,疲于奔波,满世界飞。同时,这个男人也要玩视频游戏,并且占一定时间比例。能到处飞,又能经常玩游戏的男人是什么样的男人?很显然,有生活质量,并且生活悠闲的人。我的分析,仅仅是通过可视化的数据总结的个人看法。我想,每个人的感受应该也是不尽相同。
##2.4 准备数据:数据归一化
归一化后的数据为:

从图2.5的运行结果可以看到,我们已经顺利将数据归一化了,并且求出了数据的取值范围和数据的最小值,这两个值是在分类的时候需要用到的,直接先求解出来,也算是对数据预处理了。
##3.5 测试算法:验证分类器
结果如图:
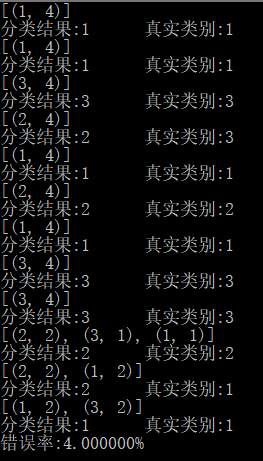
从图2.6验证分类器结果中可以看出,错误率是3%,这是一个想当不错的结果。
##3.6 使用算法:构建完整可用系统
我们可以给海伦一个小段程序,通过该程序海伦会在约会网站上找到某个人并输入他的信息。程序会给出她对男方喜欢程度的预测值。
运行程序,并输入数据(12,44000,0.5),预测结果是"你可能有些喜欢这个人",也就是这个人极具魅力。一共有三个档次:讨厌、有些喜欢、非常喜欢,对应着不喜欢的人、魅力一般的人、极具魅力的人。结果如图2.7所示。
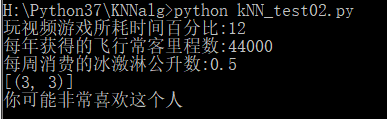
4.总结
kNN算法的优缺点
优点
简单好用,容易理解,精度高,理论成熟,既可以用来做分类也可以用来做回归;
可用于数值型数据和离散型数据;
训练时间复杂度为O(n);无数据输入假定;
对异常值不敏感。
缺点:
计算复杂性高;空间复杂性高;
样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少);
一般数值很大的时候不用这个,计算量太大。但是单个样本又不能太少,否则容易发生误分。
最大的缺点是无法给出数据的内在含义。
