Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).
You are given a target value to search. If found in the array return its index, otherwise return -1.
You may assume no duplicate exists in the array.
Your algorithm's runtime complexity must be in the order of O(log n).
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3 Output: -1
思考:一开始先熟悉题目,目的有两个:1、搞清楚题目;2、看看这样的数组有没有什么特征;
我看到题目上要求时间复杂O(logn),联想到经典问题“在有序数组里寻找指定元素”,二分法解决这个问题的本质是通过一次比较,将搜索的范围减去一半。那我可不可以用在这里呢?
当然是可以的,只不过,考虑的情况多一点点。方法如下:

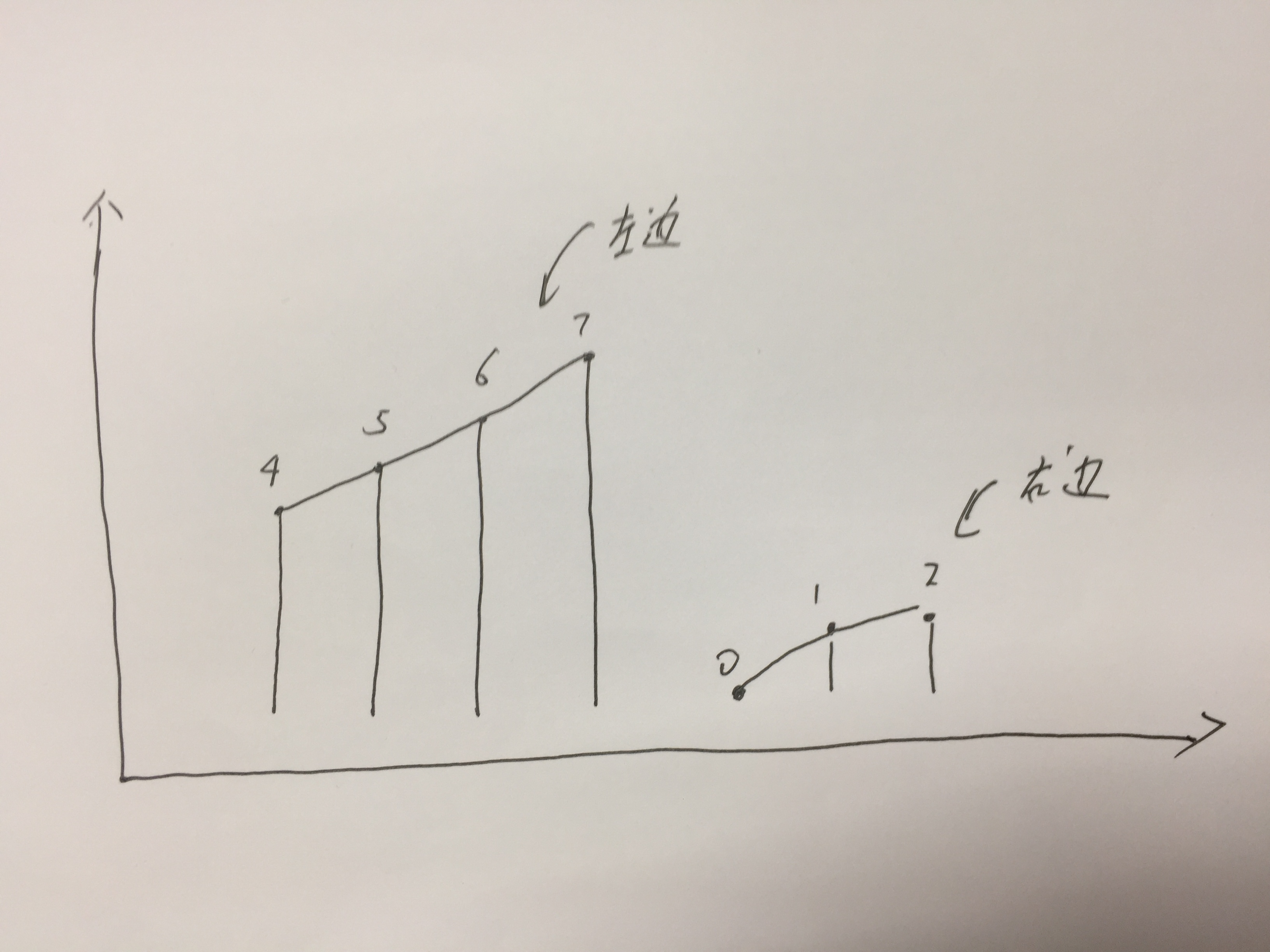
根据左边界,右边界计算出中间的值。
1、如果中间的值小于等于右边界的值,说明mid在右边
1.1 如果target等于nums[mid],直接返回
1.2 如果target大于nums[mid]并且小于等于右边界,说明target在闭区间[mid+1,右边界]
1.3 如果target大于nums[mid]并且大于右边界,说明target在闭区间[左边界,mid-1]
2、如果中间的值大于右边界的值,说明mid在左边
1.1 如果target等于nums[mid],直接返回
2.2 如果target大于nums[mid],说明target在闭区间[mid+1,右边界]
2.3 如果target小于nums[mid]并且大于等于左边界,说明target在[左边界,mid-1]
最后再考虑下特殊情况,数组长度为2,为1。总之就是不断的缩小搜索的范围。代码如下
1 class Solution { 2 public: 3 int search(vector<int>& nums, int target) { 4 5 int pre = 0; 6 int last = nums.size() - 1; 7 int mid; 8 9 while(pre<=last) { 10 mid = (pre + last) / 2; 11 if(target == nums[mid]) return mid; 12 13 if(nums[mid]<=nums[last]) { 14 //reach here means mid is in right. 15 16 if(target<nums[mid]) { 17 last = mid - 1; 18 }else { 19 if(target > nums[last]) { 20 last = mid - 1; 21 }else { 22 pre = mid + 1; 23 } 24 } 25 }else { 26 //reach here means mid is in left. 27 28 if(target > nums[mid]) { 29 pre = mid + 1; 30 }else { 31 if(target < nums[pre]) { 32 pre = mid + 1; 33 }else { 34 last = mid - 1; 35 } 36 } 37 } 38 } 39 40 return -1; 41 } 42 };