一、关于聚类及相似度、距离的知识点
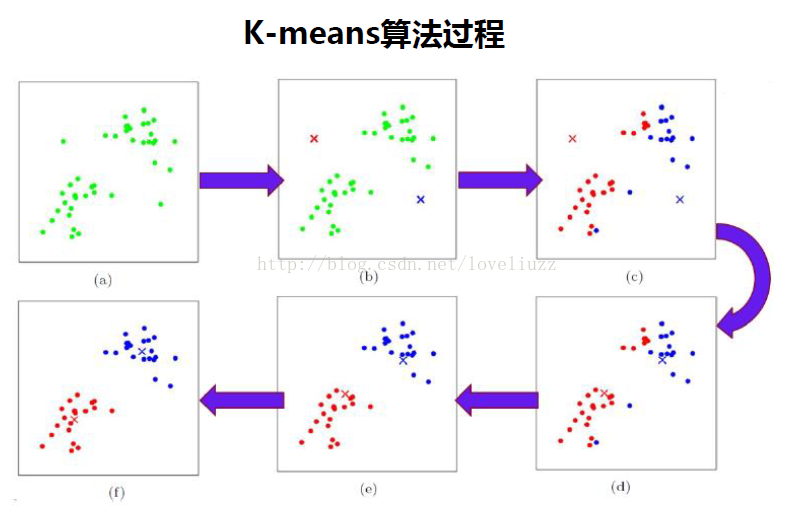
二、k-means算法思想与流程
三、sklearn中对于kmeans算法的参数
四、代码示例以及应用的知识点简介
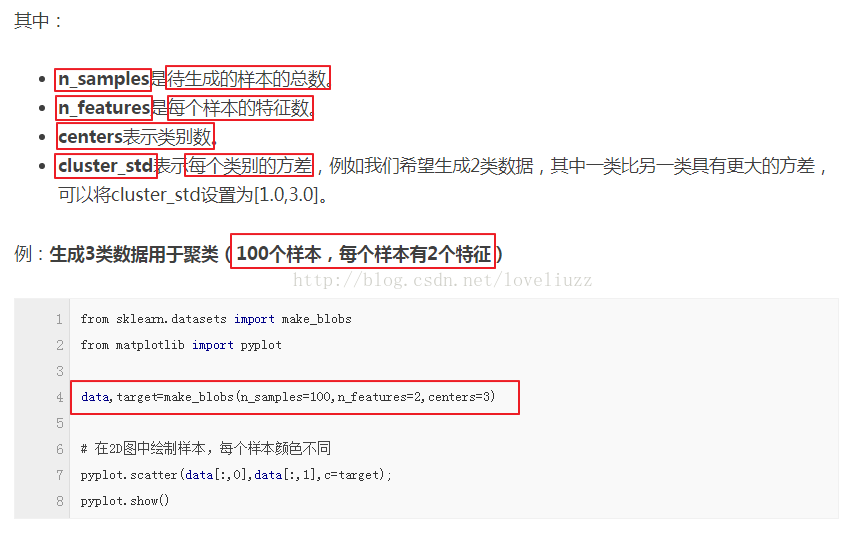
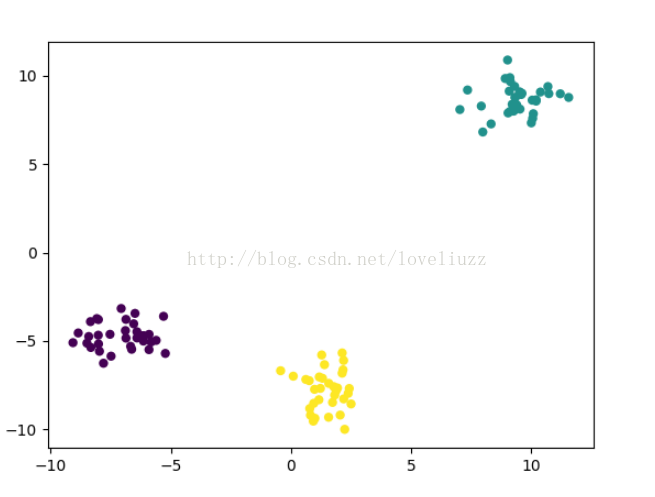
(1)make_blobs:聚类数据生成器
sklearn.datasets.make_blobs(n_samples=100, n_features=2,centers=3, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None)[source]
返回值为:
(2)np.vstack方法作用——堆叠数组
详细介绍参照博客链接:http://blog.csdn.net/csdn15698845876/article/details/73380803
- #!/usr/bin/env python
- # -*- coding:utf-8 -*-
- # Author:ZhengzhengLiu
- #k-means聚类算法
- import numpy as np
- import pandas as pd
- import matplotlib as mpl
- import matplotlib.pyplot as plt
- import matplotlib.colors
- import sklearn.datasets as ds
- from sklearn.cluster import KMeans #引入kmeans
- #解决中文显示问题
- mpl.rcParams['font.sans-serif'] = [u'SimHei']
- mpl.rcParams['axes.unicode_minus'] = False
- #产生模拟数据
- N = 1500
- centers = 4
- #make_blobs:聚类数据生成器
- data,y = ds.make_blobs(N,n_features=2,centers=centers,random_state=28)
- data2,y2 = ds.make_blobs(N,n_features=2,centers=centers,random_state=28)
- data3 = np.vstack((data[y==0][:200],data[y==1][:100],data[y==2][:10],data[y==3][:50]))
- y3 = np.array([0]*200+[1]*100+[2]*10+[3]*50)
- #模型的构建
- km = KMeans(n_clusters=centers,random_state=28)
- km.fit(data,y)
- y_hat = km.predict(data)
- print("所有样本距离聚簇中心点的总距离和:",km.inertia_)
- print("距离聚簇中心点的平均距离:",(km.inertia_/N))
- print("聚簇中心点:",km.cluster_centers_)
- y_hat2 = km.fit_predict(data2)
- y_hat3 = km.fit_predict(data3)
- def expandBorder(a, b):
- d = (b - a) * 0.1
- return a-d, b+d
- #画图
- cm = mpl.colors.ListedColormap(list("rgbmyc"))
- plt.figure(figsize=(15,9),facecolor="w")
- plt.subplot(241)
- plt.scatter(data[:,0],data[:,1],c=y,s=30,cmap=cm,edgecolors="none")
- x1_min,x2_min = np.min(data,axis=0)
- x1_max,x2_max = np.max(data,axis=0)
- x1_min,x1_max = expandBorder(x1_min,x1_max)
- x2_min,x2_max = expandBorder(x2_min,x2_max)
- plt.xlim((x1_min,x1_max))
- plt.ylim((x2_min,x2_max))
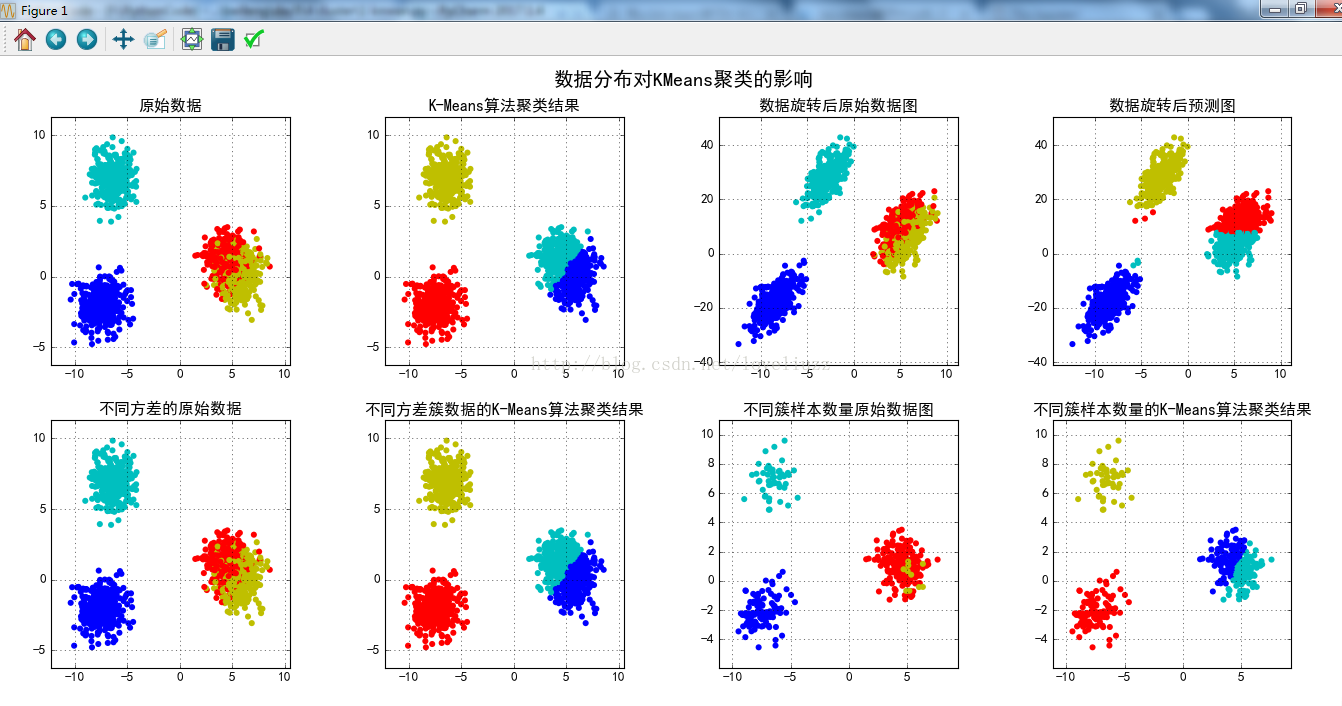
- plt.title("原始数据")
- plt.grid(True)
- plt.subplot(242)
- plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none')
- plt.xlim((x1_min, x1_max))
- plt.ylim((x2_min, x2_max))
- plt.title(u'K-Means算法聚类结果')
- plt.grid(True)
- m = np.array(((1, 1), (0.5, 5)))
- data_r = data.dot(m)
- y_r_hat = km.fit_predict(data_r)
- plt.subplot(243)
- plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
- x1_min, x2_min = np.min(data_r, axis=0)
- x1_max, x2_max = np.max(data_r, axis=0)
- x1_min, x1_max = expandBorder(x1_min, x1_max)
- x2_min, x2_max = expandBorder(x2_min, x2_max)
- plt.xlim((x1_min, x1_max))
- plt.ylim((x2_min, x2_max))
- plt.title(u'数据旋转后原始数据图')
- plt.grid(True)
- plt.subplot(244)
- plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none')
- plt.xlim((x1_min, x1_max))
- plt.ylim((x2_min, x2_max))
- plt.title(u'数据旋转后预测图')
- plt.grid(True)
- plt.subplot(245)
- plt.scatter(data2[:, 0], data2[:, 1], c=y2, s=30, cmap=cm, edgecolors='none')
- x1_min, x2_min = np.min(data2, axis=0)
- x1_max, x2_max = np.max(data2, axis=0)
- x1_min, x1_max = expandBorder(x1_min, x1_max)
- x2_min, x2_max = expandBorder(x2_min, x2_max)
- plt.xlim((x1_min, x1_max))
- plt.ylim((x2_min, x2_max))
- plt.title(u'不同方差的原始数据')
- plt.grid(True)
- plt.subplot(246)
- plt.scatter(data2[:, 0], data2[:, 1], c=y_hat2, s=30, cmap=cm, edgecolors='none')
- plt.xlim((x1_min, x1_max))
- plt.ylim((x2_min, x2_max))
- plt.title(u'不同方差簇数据的K-Means算法聚类结果')
- plt.grid(True)
- plt.subplot(247)
- plt.scatter(data3[:, 0], data3[:, 1], c=y3, s=30, cmap=cm, edgecolors='none')
- x1_min, x2_min = np.min(data3, axis=0)
- x1_max, x2_max = np.max(data3, axis=0)
- x1_min, x1_max = expandBorder(x1_min, x1_max)
- x2_min, x2_max = expandBorder(x2_min, x2_max)
- plt.xlim((x1_min, x1_max))
- plt.ylim((x2_min, x2_max))
- plt.title(u'不同簇样本数量原始数据图')
- plt.grid(True)
- plt.subplot(248)
- plt.scatter(data3[:, 0], data3[:, 1], c=y_hat3, s=30, cmap=cm, edgecolors='none')
- plt.xlim((x1_min, x1_max))
- plt.ylim((x2_min, x2_max))
- plt.title(u'不同簇样本数量的K-Means算法聚类结果')
- plt.grid(True)
- plt.tight_layout(2, rect=(0, 0, 1, 0.97))
- plt.suptitle(u'数据分布对KMeans聚类的影响', fontsize=18)
- plt.savefig("k-means聚类算法.png")
- plt.show()
- #运行结果:
- 所有样本距离聚簇中心点的总距离和: 2592.9990199
- 距离聚簇中心点的平均距离: 1.72866601327
- 聚簇中心点: [[ -7.44342199e+00 -2.00152176e+00]
- [ 5.80338598e+00 2.75272962e-03]
- [ -6.36176159e+00 6.94997331e+00]
- [ 4.34372837e+00 1.33977807e+00]]
代码中用到的知识点:
- #!/usr/bin/env python
- # -*- coding:utf-8 -*-
- # Author:ZhengzhengLiu
- #kmean与mini batch kmeans 算法的比较
- import time
- import numpy as np
- import matplotlib as mpl
- import matplotlib.pyplot as plt
- import matplotlib.colors
- from sklearn.cluster import KMeans,MiniBatchKMeans
- from sklearn.datasets.samples_generator import make_blobs
- from sklearn.metrics.pairwise import pairwise_distances_argmin
- #解决中文显示问题
- mpl.rcParams['font.sans-serif'] = [u'SimHei']
- mpl.rcParams['axes.unicode_minus'] = False
- #初始化三个中心
- centers = [[1,1],[-1,-1],[1,-1]]
- clusters = len(centers) #聚类数目为3
- #产生3000组二维数据样本,三个中心点,标准差是0.7
- X,Y = make_blobs(n_samples=300,centers=centers,cluster_std=0.7,random_state=28)
- #构建kmeans算法
- k_means = KMeans(init="k-means++",n_clusters=clusters,random_state=28)
- t0 = time.time()
- k_means.fit(X) #模型训练
- km_batch = time.time()-t0 #使用kmeans训练数据消耗的时间
- print("K-Means算法模型训练消耗时间:%.4fs"%km_batch)
- #构建mini batch kmeans算法
- batch_size = 100 #采样集的大小
- mbk = MiniBatchKMeans(init="k-means++",n_clusters=clusters,batch_size=batch_size,random_state=28)
- t0 = time.time()
- mbk.fit(X)
- mbk_batch = time.time()-t0
- print("Mini Batch K-Means算法模型训练消耗时间:%.4fs"%mbk_batch)
- #预测结果
- km_y_hat = k_means.predict(X)
- mbk_y_hat = mbk.predict(X)
- #获取聚类中心点并对其排序
- k_means_cluster_center = k_means.cluster_centers_
- mbk_cluster_center = mbk.cluster_centers_
- print("K-Means算法聚类中心点: center=",k_means_cluster_center)
- print("Mini Batch K-Means算法聚类中心点: center=",mbk_cluster_center)
- order = pairwise_distances_argmin(k_means_cluster_center,mbk_cluster_center)
- #画图
- plt.figure(figsize=(12,6),facecolor="w")
- plt.subplots_adjust(left=0.05,right=0.95,bottom=0.05,top=0.9)
- cm = mpl.colors.ListedColormap(['#FFC2CC', '#C2FFCC', '#CCC2FF'])
- cm2 = mpl.colors.ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
- #子图1——原始数据
- plt.subplot(221)
- plt.scatter(X[:,0],X[:,1],c=Y,s=6,cmap=cm,edgecolors="none")
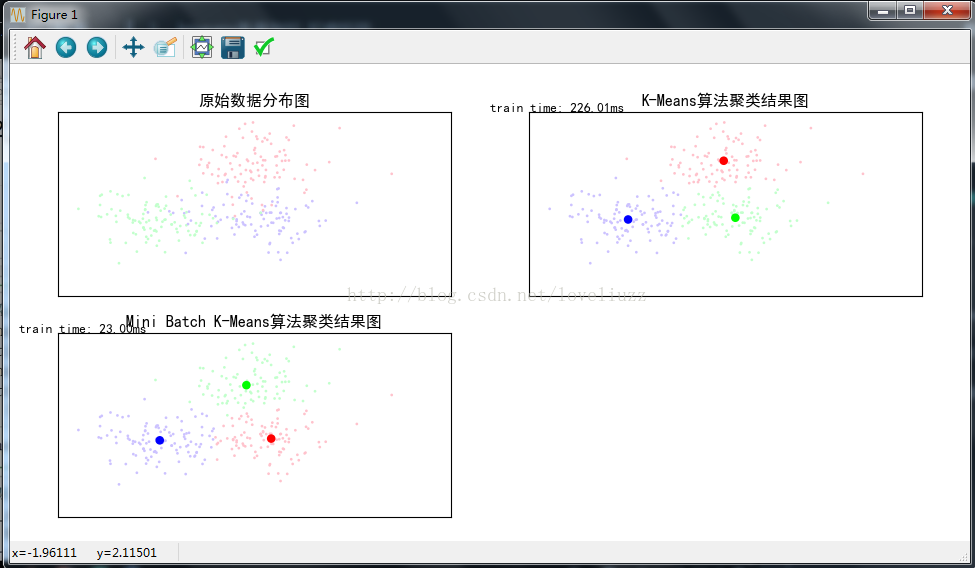
- plt.title(u"原始数据分布图")
- plt.xticks(())
- plt.yticks(())
- plt.grid(True)
- #子图2:K-Means算法聚类结果图
- plt.subplot(222)
- plt.scatter(X[:,0], X[:,1], c=km_y_hat, s=6, cmap=cm,edgecolors='none')
- plt.scatter(k_means_cluster_center[:,0], k_means_cluster_center[:,1],c=range(clusters),s=60,cmap=cm2,edgecolors='none')
- plt.title(u'K-Means算法聚类结果图')
- plt.xticks(())
- plt.yticks(())
- plt.text(-3.8, 3, 'train time: %.2fms' % (km_batch*1000))
- plt.grid(True)
- #子图三Mini Batch K-Means算法聚类结果图
- plt.subplot(223)
- plt.scatter(X[:,0], X[:,1], c=mbk_y_hat, s=6, cmap=cm,edgecolors='none')
- plt.scatter(mbk_cluster_center[:,0], mbk_cluster_center[:,1],c=range(clusters),s=60,cmap=cm2,edgecolors='none')
- plt.title(u'Mini Batch K-Means算法聚类结果图')
- plt.xticks(())
- plt.yticks(())
- plt.text(-3.8, 3, 'train time: %.2fms' % (mbk_batch*1000))
- plt.grid(True)
- plt.savefig("kmean与mini batch kmeans 算法的比较.png")
- plt.show()
- #运行结果:
- K-Means算法模型训练消耗时间:0.2260s
- Mini Batch K-Means算法模型训练消耗时间:0.0230s
- K-Means算法聚类中心点:
- center= [[ 0.96091862 1.13741775]
- [ 1.1979318 -1.02783007]
- [-0.98673669 -1.09398768]]
- Mini Batch K-Means算法聚类中心点:
- center= [[ 1.34304199 -1.01641075]
- [ 0.83760683 1.01229021]
- [-0.92702179 -1.08205992]]
五、聚类算法的衡量指标
- #!/usr/bin/env python
- # -*- coding:utf-8 -*-
- # Author:ZhengzhengLiu
- #聚类算法评估
- import time
- import numpy as np
- import matplotlib as mpl
- import matplotlib.pyplot as plt
- import matplotlib.colors
- from sklearn.cluster import KMeans,MiniBatchKMeans
- from sklearn import metrics
- from sklearn.metrics.pairwise import pairwise_distances_argmin
- from sklearn.datasets.samples_generator import make_blobs
- #解决中文显示问题
- mpl.rcParams['font.sans-serif'] = [u'SimHei']
- mpl.rcParams['axes.unicode_minus'] = False
- #初始化三个中心
- centers = [[1,1],[-1,-1],[1,-1]]
- clusters = len(centers) #聚类数目为3
- #产生3000组二维数据样本,三个中心点,标准差是0.7
- X,Y = make_blobs(n_samples=300,centers=centers,cluster_std=0.7,random_state=28)
- #构建kmeans算法
- k_means = KMeans(init="k-means++",n_clusters=clusters,random_state=28)
- t0 = time.time()
- k_means.fit(X) #模型训练
- km_batch = time.time()-t0 #使用kmeans训练数据消耗的时间
- print("K-Means算法模型训练消耗时间:%.4fs"%km_batch)
- #构建mini batch kmeans算法
- batch_size = 100 #采样集的大小
- mbk = MiniBatchKMeans(init="k-means++",n_clusters=clusters,batch_size=batch_size,random_state=28)
- t0 = time.time()
- mbk.fit(X)
- mbk_batch = time.time()-t0
- print("Mini Batch K-Means算法模型训练消耗时间:%.4fs"%mbk_batch)
- km_y_hat = k_means.labels_
- mbkm_y_hat = mbk.labels_
- k_means_cluster_centers = k_means.cluster_centers_
- mbk_means_cluster_centers = mbk.cluster_centers_
- print ("K-Means算法聚类中心点: center=", k_means_cluster_centers)
- print ("Mini Batch K-Means算法聚类中心点: center=", mbk_means_cluster_centers)
- order = pairwise_distances_argmin(k_means_cluster_centers,
- mbk_means_cluster_centers)
- #效果评估
- ### 效果评估
- score_funcs = [
- metrics.adjusted_rand_score, #ARI(调整兰德指数)
- metrics.v_measure_score, #均一性与完整性的加权平均
- metrics.adjusted_mutual_info_score, #AMI(调整互信息)
- metrics.mutual_info_score, #互信息
- ]
- ## 2. 迭代对每个评估函数进行评估操作
- for score_func in score_funcs:
- t0 = time.time()
- km_scores = score_func(Y, km_y_hat)
- print("K-Means算法:%s评估函数计算结果值:%.5f;计算消耗时间:%0.3fs" % (score_func.__name__, km_scores, time.time() - t0))
- t0 = time.time()
- mbkm_scores = score_func(Y, mbkm_y_hat)
- print("Mini Batch K-Means算法:%s评估函数计算结果值:%.5f;计算消耗时间:%0.3fs " % (score_func.__name__, mbkm_scores, time.time() - t0))
- #运行结果:
- K-Means算法模型训练消耗时间:0.6350s
- Mini Batch K-Means算法模型训练消耗时间:0.0900s
- K-Means算法聚类中心点:
- center= [[ 0.96091862 1.13741775]
- [ 1.1979318 -1.02783007]
- [-0.98673669 -1.09398768]]
- Mini Batch K-Means算法聚类中心点:
- center= [[ 1.34304199 -1.01641075]
- [ 0.83760683 1.01229021]
- [-0.92702179 -1.08205992]]
- K-Means算法:adjusted_rand_score评估函数计算结果值:0.72566;计算消耗时间:0.071s
- Mini Batch K-Means算法:adjusted_rand_score评估函数计算结果值:0.69544;计算消耗时间:0.001s
- K-Means算法:v_measure_score评估函数计算结果值:0.67529;计算消耗时间:0.004s
- Mini Batch K-Means算法:v_measure_score评估函数计算结果值:0.65055;计算消耗时间:0.004s
- K-Means算法:adjusted_mutual_info_score评估函数计算结果值:0.67263;计算消耗时间:0.006s
- Mini Batch K-Means算法:adjusted_mutual_info_score评估函数计算结果值:0.64731;计算消耗时间:0.005s
- K-Means算法:mutual_info_score评估函数计算结果值:0.74116;计算消耗时间:0.002s
- Mini Batch K-Means算法:mutual_info_score评估函数计算结果值:0.71351;计算消耗时间:0.001s