目录
举例
在Inception module上的应用
参考资料
可以减少计算量,可以增加非线性判别能力
|
举例 |
假设有1个高为30、宽为40,深度为200的三维张量与55个高为5、宽为5、深度为200的卷积核same卷积,步长=1,则结果是高为30、宽为40、深度为55的三维张量,如图所示:

该卷积过程的乘法计算量大约为5*5*200*30*40*55=330000000,这个计算量很大。
接着,我们可以考虑第二种卷积过程,先利用1*1的卷积核在深度上降维,然后升维:
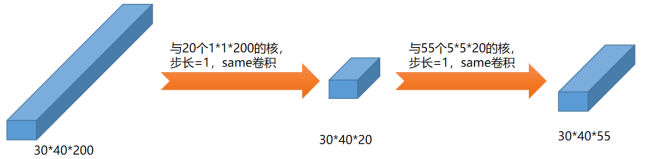
上述卷积过程的计算量大约为:
第一步:1*1*200*30*40*20=4800000
第二步:5*5*20*30*40*55=33000000
总的乘法计算量大约为:37800000
显然,得到同样的最终的结果,采用第二种方式,即首先在深度方向上降维,第二种的计算量是第一种的37800000/330000000=0.11。
第二步中的中间层也可以叫做瓶颈层,因为他是整个网络中最小的,你可能会问:你这样大幅地缩小模型的规模会不会影响到网络的性能?事实证明只要合理构建瓶颈层,你既可以显著缩小瓶颈层规模,又不会降低网络性能,从而大量减少了计算。
另外,因为又引入了一层结构,激活函数可以引入额外的非线性能力.
|
在Inception module上的应用 |
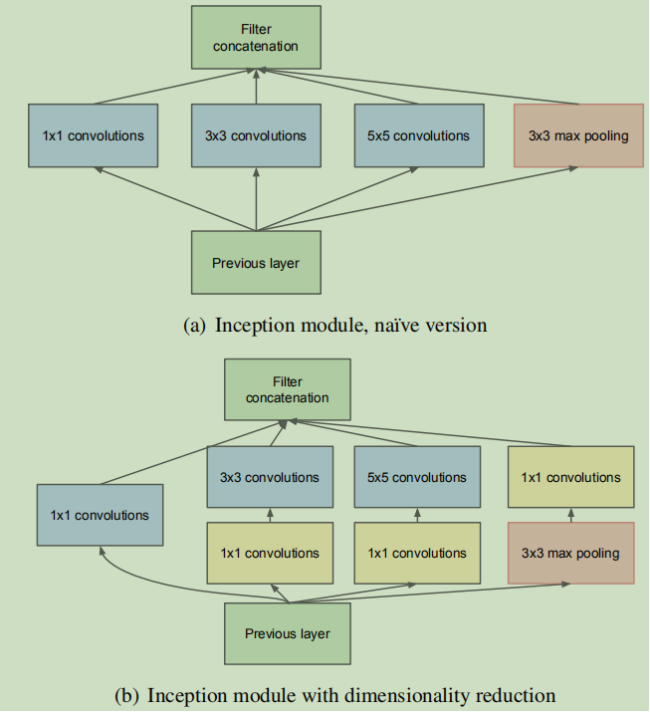
在googlenet中的inception module中就使用了这种1*1的卷积核做降维,以减少计算量和增加非线性判别能力
|
参考资料 |
《图解深度学习与神经网络:从张量到TensorFlow实现》_张平
inceptionV1-Going Deeper with Convolutions
《深-度-学-习-核-心-技-术-与-实-践》
吴恩达深度学习