目录
一元线性回归模型
一元线性回归代价函数图像
梯度下降求解
SGD、BGD、Mini-batchGD的特点
参考资料
在《深度学习面试题03改进版梯度下降法Adagrad、RMSprop、Momentum、Adam》中讲到了多种改进的梯度下降公式。而这篇文章和03篇描述的不是一个事情,我们从一个例子说起,就知道改良的GD算法和本节介绍的GD算法的不同点了。
|
一元线性回归模型 |
举例:以房屋面积预测房屋价格
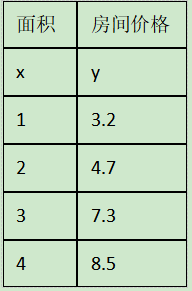
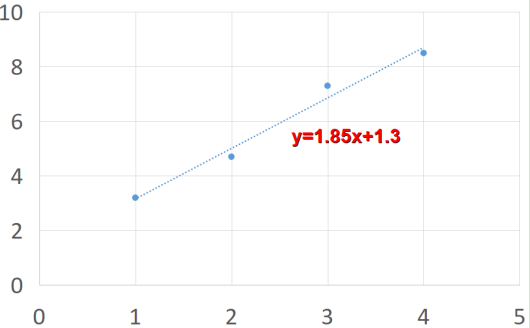
假设函数可以设置为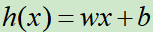
|
一元线性回归代价函数图像 |
每一个预测值都与真实值存在一个差距,差距的平方和就可以作为一个代价函数。
因此代价函数为:
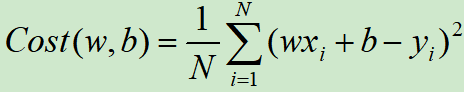
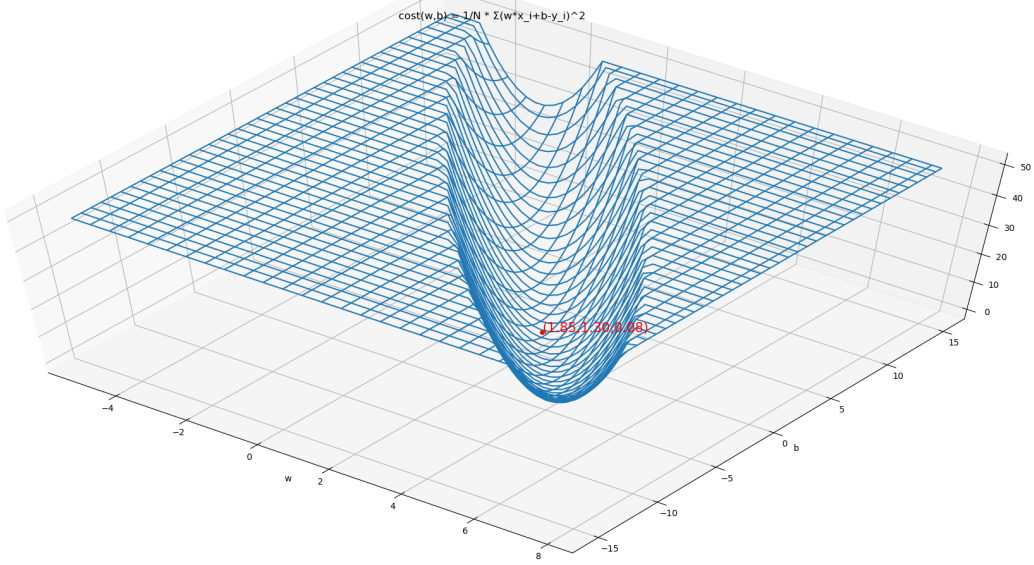
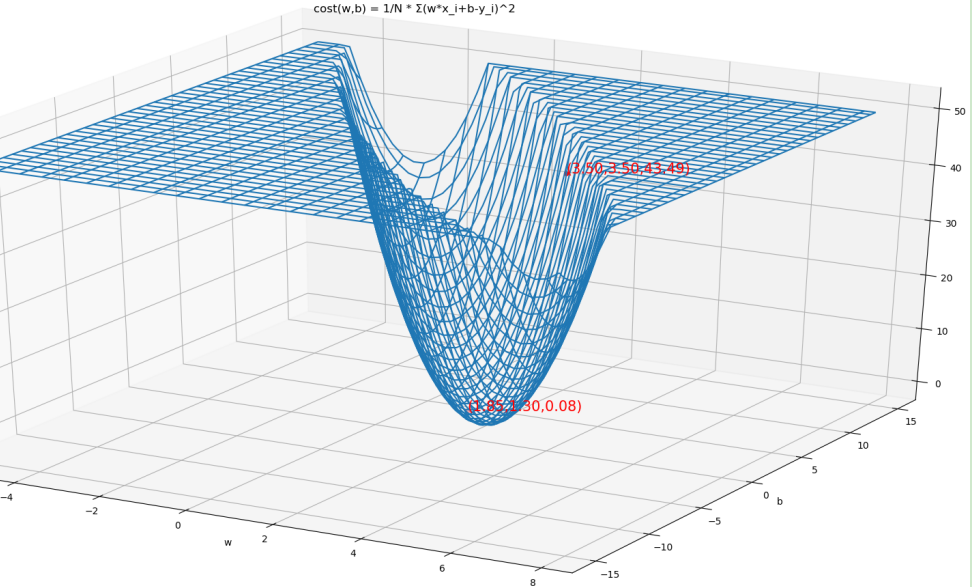
如下图所示(为方便观察,做了一个截断)

代码为:
 View Code
View Code|
梯度下降求解 |
当使用梯度下降法求解时,假设初始化(w,b)=(3.5,3.5)
代价函数关于w和b的偏导数为:
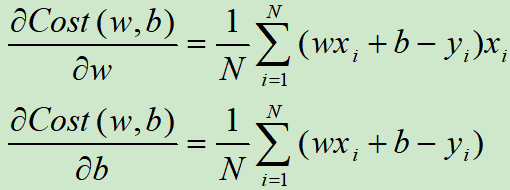
重点来了:Adagrad、RMSprop、Adam等算法都是建立在偏导数之上的,他们并不关心上式中N的取值,N取1,取100,还是取N,Adagrad、RMSprop、Adam等算法都可以运行。
而随机梯度下降法(Stochastic Gradient Descent,SGD),批量梯度下降法(Batch Gradient Descent,BGD),小批量梯度下降法(Mini-batch Gradient Descent,Mini-batchGD)则是研究这里的N的大小的。
如果N=1,此时为SGD,计算代价函数梯度的时候只考虑一个样本;
如果N=样本容量,此时为BGD,计算代价函数梯度的时候考虑全部样本;
如果N=m,1<m<N,此时为Mini-batchGD,计算代价函数梯度的时候考虑一小批样本。
|
SGD、BGD、Mini-batchGD的特点 |
SGD计算根据随机一个样本构造出来的代价函数的梯度,这与计算根据全部样本构造出来的代价函数的梯度肯定有偏差,也许是一个不好的梯度方向,下降时候并不沿着最有的方向下降,但是优点是可以快速的计算一个近似梯度,因为计算量缩减到原来的1/N。
BGD计算根据全部样本的构造出来的代价函数的梯度,方向肯定是沿着当前最优的下降方向,但是计算代价较高,当数据集较大时,相当耗时。
Mini-batchGD就不用说了,是前两者的折中
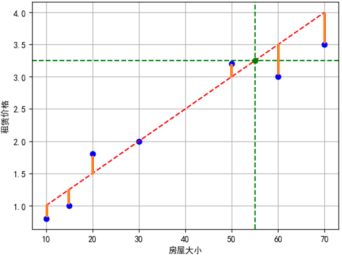
下面用图像演示一下BGD和SGD下降的过程
BGD效果如下
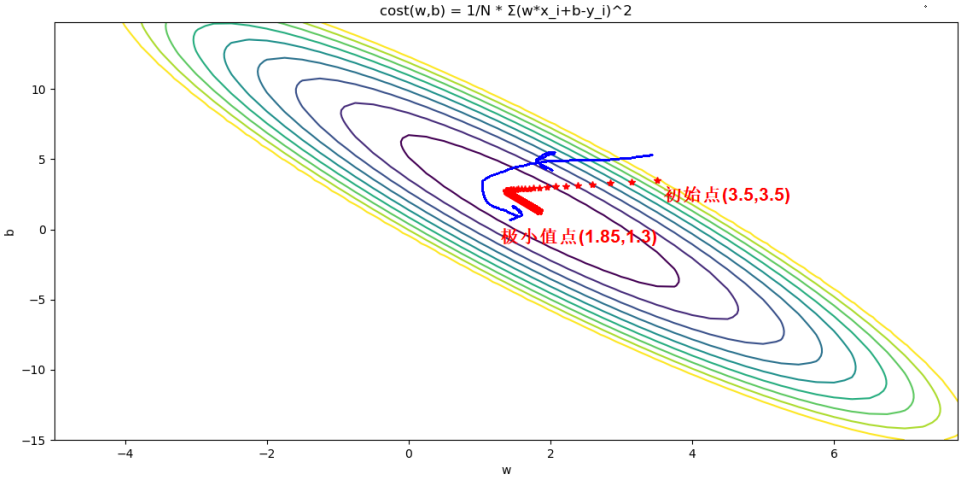
BGD代码如下:
 View Code
View CodeSGD效果如下:
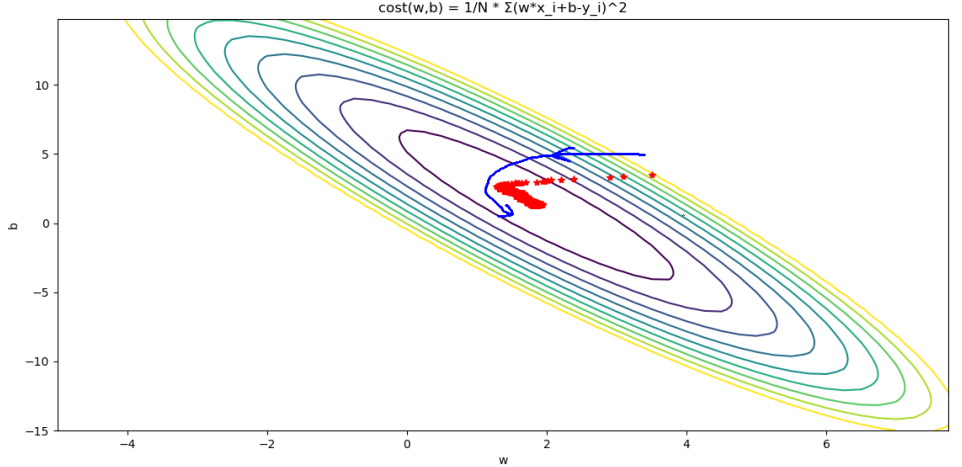
很明显SGD在下降过程中存在方向不稳定的情况,但是最终还是能收敛到最优点
SGD代码如下:
 View Code
View Code|
参考资料 |
《图解深度学习与神经网络:从张量到TensorFlow实现》_张平