Java后缀数组-求sa数组

后缀数组的一些基本概念请自行百度,简单来说后缀数组就是一个字符串所有后缀大小排序后的一个集合，然后我们根据后缀数组的一些性质就可以实现各种需求。

public class MySuffixArrayTest {

    public char[] suffix;//原始字符串

    public int n;//字符串长度

    public int[] rank;// Suffix[i]在所有后缀中的排名

    public int[] sa;// 满足Suffix[SA[1]] < Suffix[SA[2]] …… < Suffix[SA[Len]],即排名为i的后缀为Suffix[SA[i]]
                    // (与Rank是互逆运算)

    public int[] height;// 表示Suffix[SA[i]]和Suffix[SA[i - 1]]的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀

    public int[] h;// 等于Height[Rank[i]]，也就是后缀Suffix[i]和它前一名的后缀的最长公共前缀

    public int[] ws;// 计数排序辅助数组

    public int[] y;// 第二关键字rank数组

    public int[] x;// rank的辅助数组
｝

以下的讲解都以"aabaaaab"这个字符串为例，先展示一下结果，请参考这个结果进行理解分析（这个结果图我复制别人的，请各位默认下标减1，因为我的数组从下标0开始的）

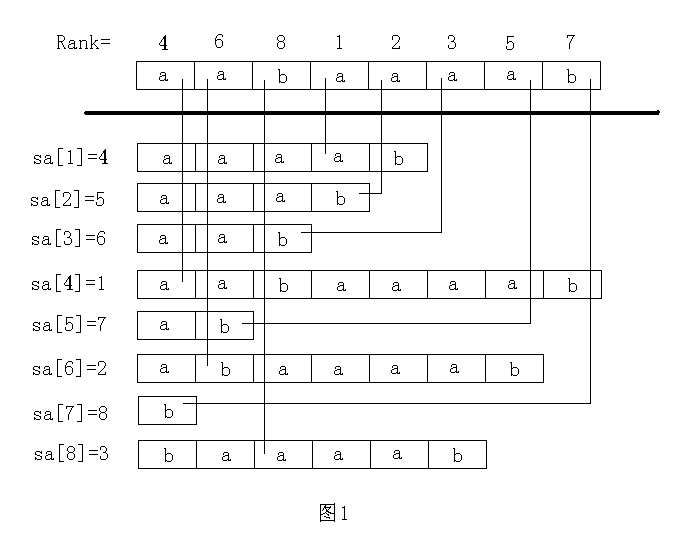
suffix：原始字符串数组  假设原始字符串是"aabaaaab"  那这个数组对应的值应该是{'a','a','b','a','a','a','a','b'}
n：字符串长度　这里n是8
rank: 后缀数组的名次数组  相当于存的是第i个后缀对应的名次是多少  比如rank[0]就是指"aabaaaab"这个后缀的名次  rank[1]指"abaaaab"这个后缀的名次
sa: 这个是和rank数组互逆的一个数组  存的是第x名的是哪个后缀  还是举例子来说明  sa[0]指的是排名第一的后缀数组即为3  也就是"aaaab"这个数组  他对应的rank[3]就是0。 sa[rank[i]]=i 这个式子请务必理解，理解了这个sa和rank的关系你应该也搞懂了  
height: height[i]就是sa[i]后缀数组和sa[i-1]后缀数组的最大公共前缀的长度  height[1]指的是排名第2和排名第1的最大公共前缀 sa[1]与sa[0]即"aaab"与"aaaab"的最大公共前缀 自然一眼看出 height[1]=3
h: h[i]指的是第i个后缀与他前一名的最大公共前缀  h[0]指的就是第一个后缀数组即"aabaaaab"与他前一名即"aab"的最大公共前缀 也就是height[rank[0]]=height[3]=3 这个有点不好理解 可以暂时不理解 继续往下看
ws: 没什么好说的，计数排序的辅助数组
y: 存的是第二关键字排序  相当于第二关键字的sa数组
x: 你可以理解为rank数组的备份，他最开始是rank数组备份，之后记录每次循环后的rank数组

首先来看下求sa数组的代码，我会一段一段的说明代码作用并在后面附上总代码

        rank = new int[n];
        sa = new int[n];
        ws = new int[255];
        y = new int[n];
        x = new int[n];
        // 循环原字符串转换int值放入rank数组
        for (int i = 0; i < n; i++) {
            rank[i] = (int) suffix[i];
        }         

上面这段代码的作用就是初始化数组以及进行第一次计数排序，第一次循环是对rank数组赋初值，执行完后rank数组对应值为{97,97,98,97,97,97,97,98},大家应该看得出来rank数组的初值就是字母对应的ascii码。

接下来的三段循环就是第一次计数排序了，不理解计数排序的请百度。我说下这三段循环运行的过程

for (int i = 0; i < n; i++) {
            ws[rank[i]]++;
            x[i] = rank[i];
        }
for (int i = 1; i < ws.length; i++) {
            ws[i] += ws[i - 1];
        }

这两段循环做的是对所有出现值计数，并备份rank数组至x数组，第一个循环运行完后ws[97]=6,ws[98]=2，第二个循环运行完后ws[97]=6,ws[98]=8

for (int i = n - 1; i >= 0; i--) {
            sa[--ws[rank[i]]] = i;
        }

上面这段就是具体的计数排序求sa数组的代码，大家第一次看的时候肯定是蒙的，这怎么就求出了sa呢。我第一次也是蒙的，但请保持耐心，仔细理解这段代码。还记得前面说的公式吗 sa[rank[i]]=i  举个例子对于后缀"b"我们求他的sa  即sa[rank[7]]=sa[98]=7，显然sa[98]不存在， 但我们将98出现的次数已经记录在ws数组了 (请务必先理解计数排序，否则这里以及之后你都会看不明白)，那么ws[98]应该就是"b"对应的名次了  ，注意不要忘记计数减1  ，就变成了 sa[--ws[rank[i]]] = i(我这里是先减，这也是我的下标比图上少1的原因)。至于为什么要从后向前遍历，这里你需要仔细理解一下，否则后面根据第二关键字进行排序的方式你肯定会完全蒙蔽。如果有两个rank值相同的你怎么排序呢？肯定是先出现的后缀在sa数组的前面，仔细思考这个循环以及ws数组值的变化，你会明白，for循环的顺序实际上代表了rank值相同时的排列顺序。从后向前遍历代表了rank值相同时靠后的后缀排名也靠后。

以上只是第一次计数排序，相当于只比较每个后缀数组的首字母求出了一个sa,对应的结果如下图

// 循环组合排序
        for (int j = 1, p = 0; j <= n; j = j << 1) {
            // 需要补位的先加入排序数组y
            p = 0;
            for (int i = n - j; i < n; i++) {
                y[p++] = i;
            }
            // 根据第一关键字sa排出第二关键字
            for (int i = 0; i < n; i++) {
                if (sa[i] >= j) {
                    y[p++] = sa[i] - j;
                }
            }

            // 合并两个关键字的排序
            for (int i = 0; i < ws.length; i++) {
                ws[i] = 0;
            }
            for (int i : x) {
                ws[i]++;
            }
            for (int i = 1; i < ws.length; i++) {
                ws[i] += ws[i - 1];
            }
            for (int i = n - 1; i >= 0; i--) {
                sa[--ws[x[y[i]]]] = y[i];
                y[i] = 0;
            }

            // 根据sa算出rank数组
            int xb[] = new int[n];// x数组备份
            for (int i = 0; i < n; i++) {
                xb[i] = x[i];
            }
            int number = 1;
            x[sa[0]] = 1;
            for (int i = 1; i < n; i++) {
                if (xb[sa[i]] != xb[sa[i - 1]]) {
                    x[sa[i]] = ++number;
                } else if (sa[i] + j >= n && sa[i - 1] + j >= n) {
                    x[sa[i]] = number;
                } else if (sa[i] + j < n && sa[i - 1] + j >= n) {
                    x[sa[i]] = ++number;
                } else if (xb[sa[i] + j] != xb[sa[i - 1] + j]) {
                    x[sa[i]] = ++number;
                } else {
                    x[sa[i]] = number;
                }
                if (number >= n)
                    break;
            }
        }

上面的代码是循环组合排序，这是求sa数组最难以理解的一段代码，首先大家需要理解一下倍增算法的思路。第一次计数排序后我们是不是已经知道了所有后缀数组第一个首字母的排序，既然我们知道了第一个首字母的排序那是不是相当于我们也知道了他第二个字母的顺序(注意排序和顺序的区别，排序是我们知道他固定的排在第几名，顺序是我们只知道他出现的次序，但并不知道他具体排第几名)，这是当然的,因为他们本来就是出自一个字符串，对于每个后缀他同时也可以作为他之前后缀的后缀。说起来绕口，举个例子，比如对于"baaaab"他首字母的顺序是不是对应"abaaaab"的第二关键字顺序。我们有了第一关键字的排序和第二关键字的排序就能求出两个关键字的组合排序，跟据组合排序的结果我们还是可以延用之前的想法，对于"baaaab"第一次组合排序后我们排出来他头两个字母"ba"的排序，那么他同时他也可以作为"aabaaaab"的第二关键字的顺序。大家应该能看出每次循环关键字都是乘2的关系，这就是倍增算法。整个排序的逻辑参考下图

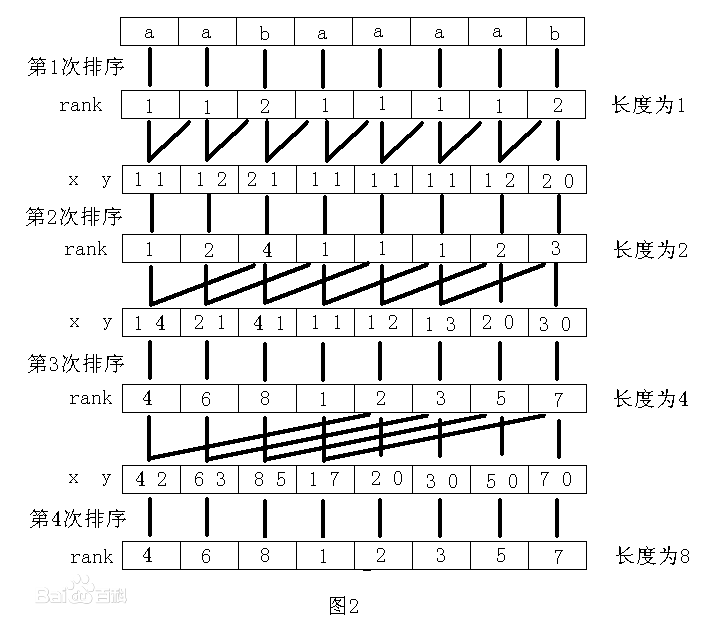
然后我们来分段的分析代码

for (int i = n - j; i < n; i++) {
                y[p++] = i;
            }
            // 根据第一关键字sa排出第二关键字
for (int i = 0; i < n; i++) {
                if (sa[i] >= j) {
                    y[p++] = sa[i] - j;
                }
            }

以上代码就是求第二关键字的sa也就是y数组，p初始值为0，第一段循环是将需要补位的后缀排在数组最前面。这是当然的，需要补位意味着没有第二关键字，自然排在前几名，比如第一次循环时，y[0]=7，也就是第二关键字的第一名是后缀"b"，显而易见，"b"的第二关键字没有所以排在前面。

第二个循环的逻辑你需要结合前面的逻辑图进行理解了，我们对第一关键字的排序结果sa进行遍历(想一下我们为什么对sa进行遍历？sa是已排好的第一关键字排序，遍历他并根据每一个后缀求出他对应的作为第二关键字的后缀自然肯定也是有序的)，if(sa[i] >=j )判断该后缀能否作为其他后缀的第二关键字，以第一次循环j=1为例，当sa[i]=0时代表后缀数组"aabaaaab"，显然它无法作为其他后缀的第二关键字。对于可以作为其他后缀第二关键字的，他sa的顺序就是对应的第二关键字的顺序，sa[i] - j 求出他作为第二关键字的后缀放在y数组下，并且p++。这里你需要慢慢理解。

// 合并两个关键字的排序
            for (int i = 0; i < ws.length; i++) {
                ws[i] = 0;
            }
            for (int i : x) {
                ws[i]++;
            }
            for (int i = 1; i < ws.length; i++) {
                ws[i] += ws[i - 1];
            }
            for (int i = n - 1; i >= 0; i--) {
                sa[--ws[x[y[i]]]] = y[i];
                y[i] = 0;
            }

以上是根据第一关键字排序sa和第二关键字排序y求出其组合排序，这段代码相当的晦涩难懂。我们可以先不理解代码，先理解一个思路，对于两个关键字排序，实际规则和两个数字排序差不多，比如11和12比较大小，10位就是第一关键字，个位就是第二关键字，比较完10位我们求得11=12，再比较个位我们知道11<12，10位相同的话其个位的顺序就是大小顺序。我上面第一次计数排序时说过，计数排序for循环的顺序实际上代表了rank值相同时的排列顺序，那么这里我们怎么一次计数排序就求出两个关键字合并后的顺序呢？我说下我的理解，一次计数排序实际上包含了两次排序，一次是数值的排序，一次是出现次序的排序，其规则就相当于前面11和12比较的例子，数值的排序是10位，出现次序的排序是个位。到这里我们就有思路了，数值的排序用第一关键字的排序，出现次序的排序用第二关键字的排序，这样就能一次计数排序求得两个关键字合并后的排序。上面的代码就是这个思路的实现。x数组就是第一关键字的rank数组，对x数组计数的过程就是对数值的排序。

for (int i = n - 1; i >= 0; i--) {
                sa[--ws[x[y[i]]]] = y[i];
                y[i] = 0;
            }

这第三段循环是上面思路实现的精髓，我们对第二关键字数组y从后进行遍历，这就相当于是出现次序的排序，对于y[i]我们求出他第一关键字的计数排名，这个第一关键字的计数排名就是y[i]的排名，最后计数减1。合并关键字的排序成功求出。

相信你如果理解了上面所有的代码后肯定会拍案叫绝，我本人在一遍遍琢磨这段代码时也是热血澎湃，简直拜服了。这就是算法的魅力吧。

有了sa数组我们就可以求rank数组，这并不难，也就不讲解了。下面附上求sa的所有代码。之后我还会写一篇求height数组的讲解以及后缀数组的一些简单应用。

public static void main(String[] args) {
        String str = "aabaaaab";
        MySuffixArrayTest arrayTest = new MySuffixArrayTest(str.toString());
        arrayTest.initSa();// 求sa数组
    }

    public void initSa() {
        rank = new int[n];
        sa = new int[n];
        ws = new int[255];
        y = new int[n];
        x = new int[n];
        // 循环原字符串转换int值放入rank数组
        for (int i = 0; i < n; i++) {
            rank[i] = (int) suffix[i];
        }
        // 第一次计数排序
        for (int i = 0; i < n; i++) {
            ws[rank[i]]++;
            x[i] = rank[i];
        }
        for (int i = 1; i < ws.length; i++) {
            ws[i] += ws[i - 1];
        }
        for (int i = n - 1; i >= 0; i--) {
            sa[--ws[rank[i]]] = i;
        }
        // 循环组合排序
        for (int j = 1, p = 0; j <= n; j = j << 1) {
            // 需要补位的先加入排序数组y
            p = 0;
            for (int i = n - j; i < n; i++) {
                y[p++] = i;
            }
            // 根据第一关键字sa排出第二关键字
            for (int i = 0; i < n; i++) {
                if (sa[i] >= j) {
                    y[p++] = sa[i] - j;
                }
            }

            // 合并两个关键字的排序
            for (int i = 0; i < ws.length; i++) {
                ws[i] = 0;
            }
            for (int i : x) {
                ws[i]++;
            }
            for (int i = 1; i < ws.length; i++) {
                ws[i] += ws[i - 1];
            }
            for (int i = n - 1; i >= 0; i--) {
                sa[--ws[x[y[i]]]] = y[i];
                y[i] = 0;
            }

            // 根据sa算出rank数组
            int xb[] = new int[n];// x数组备份
            for (int i = 0; i < n; i++) {
                xb[i] = x[i];
            }
            int number = 1;
            x[sa[0]] = 1;
            for (int i = 1; i < n; i++) {
                if (xb[sa[i]] != xb[sa[i - 1]]) {
                    x[sa[i]] = ++number;
                } else if (sa[i] + j >= n && sa[i - 1] + j >= n) {
                    x[sa[i]] = number;
                } else if (sa[i] + j < n && sa[i - 1] + j >= n) {
                    x[sa[i]] = ++number;
                } else if (xb[sa[i] + j] != xb[sa[i - 1] + j]) {
                    x[sa[i]] = ++number;
                } else {
                    x[sa[i]] = number;
                }
                if (number >= n)
                    break;
            }
        }
    }