堆排序的时间复杂度是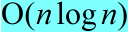 ,具有空间原址性,即任何时候都只需要常数个额外的元素空间存储临时数据。
,具有空间原址性,即任何时候都只需要常数个额外的元素空间存储临时数据。
一、堆
二叉堆是一个数组,可看成一个近似的完全二叉树,树上的每个结点对应数组中的一个元素。除了最底层外,该树是完全充满的,而且是从左到右填充。

二叉堆可以分为两种形式:最大堆和最小堆。在最大堆中除根节点外所有结点i都要满足: ,即某个结点的值至多与其父结点一样大。在最小堆中除根节点外所有结点i都要满足:
,即某个结点的值至多与其父结点一样大。在最小堆中除根节点外所有结点i都要满足: 。
。
说明:堆排序中,我们使用最大堆,最小堆通常用于构造优先队列。
二、维护堆的性质
函数MAX-HEAPIFY的输入为一个数组A和下标i,假定根节点为LEFT(i)和RIGHT(i)的二叉树都是最大堆,通过让A[i]的值在最大堆中逐级下降,从而使得以下标i为根结点的子树为最大堆。
函数MAX-HEAPIFY的时间代价包括:调整A[i]、A[LEFT[i]]和A[RIGHT[i]]关系的时间代价 ,加上以一颗i的一个孩子为根结点的子树上运行MAX-HEAPIFY的时间代价(假设递归调用会发生)。
,加上以一颗i的一个孩子为根结点的子树上运行MAX-HEAPIFY的时间代价(假设递归调用会发生)。
下面首先证明每个子树的大小至多为2n/3。
证明:设堆的高度为h,最后一层结点个数为m,则整个堆的结点总数为: 。
。
根结点的左子树结点总数为: ,
,
根结点的右子树结点总数为: ,其中
,其中 。
。
当最底层恰好半满的时候, ,则
,则 ,
, 。
。
解出: ,
, 。
。
因此,每个子树的大小至多为2n/3(最坏情况发生在树的最底层恰好半满的时候),MAX-HEAPIFY的运行时间为:
 ,解出
,解出 。
。
三、建堆
可以利用自底向上的方法利用MAX-HEAPIFY把一个大小为n的数组转换为最大堆,子数组A[n/2+1…n]中的元素都是叶子结点,每个叶子结点可看成只包含一个元素的堆。
可以简单估算函数BUILD-MAX-HEAP运行时间的上界。每次调用MAX-HEAPIFY的时间复杂度是 ,BUILD-MAX-HEAP需要
,BUILD-MAX-HEAP需要 次这样的调用,因此总的时间复杂度是
次这样的调用,因此总的时间复杂度是 。
。
说明:
(1)这个上界虽然正确,但不是渐进准确的。因为不同结点运行MAX-HEAPIFY的时间与该结点的高度有关,且大部分结点高度都很小。可以证明能够在线性时间内 ,把一个无序数组构造成为一个最大堆。
,把一个无序数组构造成为一个最大堆。
(2)也可以通过调用BUILD-MIN-HEAP在线性时间内,把一个无序数组构造成为一个最小堆。BUILD-MIN-HEAP与BUILD-MAX-HEAP完全相同。
(3)因为有n个结点,最后一个元素序号为n,那么它的parent结点应该是序号最大的parent结点,那么这个parent结点就为[n/2],其之后都是叶子结点,为[n/2] + 1, [n/2] + 2, ..., n。
四、堆排序算法
思路:初始时,利用BUILD-MAX-HEAP将数组A[1…n]建成最大堆。因为数组中最大元素总在根结点A[1]中,通过它与A[n]进行互换,可让最大元素放到正确的位置。然后,从堆中去掉结点n,剩余结点中,原来根的孩子结点仍然是最大堆,新的根结点可能会违背最大堆的性质。为了维护最大堆的性质,调用MAX-HEAPIFY(A,1),从而在A[1…n-1]上构造一个新的最大堆。堆排序算法会不断重复这个过程,直到堆的大小由n-1降为2。
HEAPSORT过程的时间复杂度是 ,因为每次调用BUILD-MAX-HEAP的时间复杂度是
,因为每次调用BUILD-MAX-HEAP的时间复杂度是 ,而n-1次调用
,而n-1次调用
MAX-HEAPIFY,每次的时间为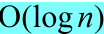 。
。
下面给出堆排序算法的参考程序:
1 #include <iostream> 2 using namespace std; 3 4 #define LEFT(i) 2 * i 5 #define RIGHT(i) 2 * i + 1 6 7 class MaxHeap 8 { 9 public: 10 void BuildMaxHeap(int *A, int len); 11 void MaxHeapfy(int *A, int i, int len); 12 void HeapSort(int *A, int len); 13 }; 14 15 void MaxHeap::MaxHeapfy(int *A, int i, int len) 16 { 17 int left = LEFT(i); 18 int right = RIGHT(i); 19 int large; 20 21 if (left <= len && A[left - 1] > A[i - 1]) 22 { 23 large = left; 24 } 25 else 26 { 27 large = i; 28 } 29 30 if (right <= len && A[right - 1] > A[large - 1]) 31 { 32 large = right; 33 } 34 35 if (i != large) 36 { 37 int tmp = A[i - 1]; 38 A[i - 1] = A[large - 1]; 39 A[large - 1] = tmp; 40 41 MaxHeapfy(A, large, len); 42 } 43 } 44 45 void MaxHeap::BuildMaxHeap(int *A, int len) 46 { 47 for (int i = len / 2; i > 0; --i) 48 { 49 MaxHeapfy(A, i, len); 50 } 51 } 52 53 void MaxHeap::HeapSort(int *A, int len) 54 { 55 BuildMaxHeap(A, len); 56 57 for (int i = len; i > 1; --i) 58 { 59 int tmp = A[0]; 60 A[0] = A[i - 1]; 61 A[i - 1] = tmp; 62 63 MaxHeapfy(A, 1, i - 1); 64 } 65 } 66 67 //Test 68 int main() 69 { 70 MaxHeap Test; 71 int A[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}; 72 73 Test.HeapSort(A, 10); 74 for (int i = 0; i < 10; ++i) 75 { 76 cout << A[i] << " "; 77 } 78 cout << endl; 79 80 return 0; 81 }