神经网络学习之----单层感知器

神经元：通常是由一个神经细胞都有树突、轴突、细胞核等等。树突可以接受其他神经元传来的信号，然后对这些信号进行一下处理传递给下一个神经元。

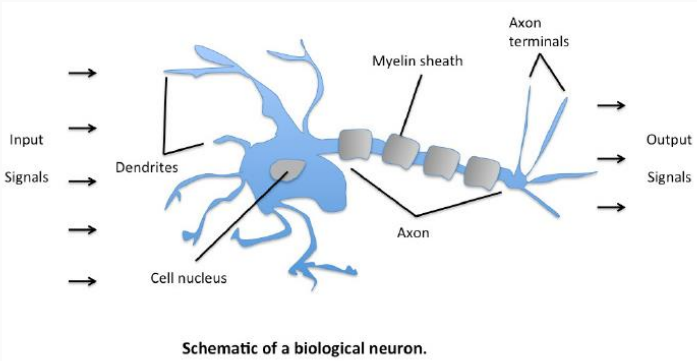
单层感知器：1958年，美国心理学家Frank Rosenblatt 提出一种具有单层计算单元的神经网络，成为Perceptron，即感知器。单层感知器即只有一层处理单元的感知器，如果包括输入层在内，应为两层。

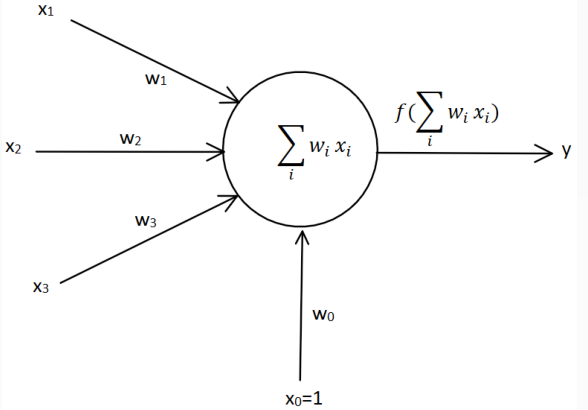
其中x1、x2，x3属于输入层，w1，w2，w3分别数x的权值，b代表了偏置。当外部信号X通过神经传递到神经元经过神经元进行处理，就相当于x1*w1+x2*w2+x3*w3+b。当神经元处理过后对外部进行输入，在输出的过程中经过了一个激活函数f，单层感知器的激活函数就是sign（x），最后形成了输出y。其作用就是处理简单的函数，进行分类处理。

单层感知器举例：

把偏置当做特殊权值：添加x0为输入，w0作为x0的权值，结果就相当于把x1*w1+x2*w2+x3*w3+b改成了x0*w0+x1*w1+x2*w2+x3*w3

感知器学习规则：大1958年，美国学者Frank Rosenblatt首次定义了一个具有单层计算单元的神经网络结构，称为Perceptron（感知器）。感知器的学习规则规定，学习信号等于神经元期望输出（教师信号）与实际输出之差：

　　

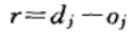
式中，dj为期望的输出，oj = f (Wj^T X)。感知器采用了符号函数作为转移函数，其表达为：

　　

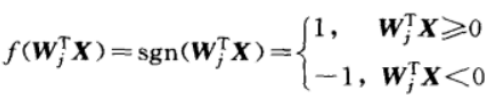
因此，权值调整公式应为：

　　

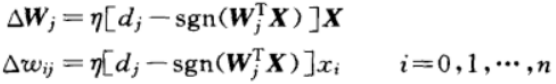
式中，当实际输出与期望值相同时，权值不需要调整；在有误差存在的情况下，由于dj和sgn(Wj^T X)属于{-1,1}，权值调整公式可简化为：

　　

感知器学习规则只适用于二进制神经元，初始权值可取任意值。

感知器学习规则代表一种有导师学习，由于感知器理论是研究其他神经网络的基础，该规则对于神经网络的有导师学习具有极为重要的意义。

学习率(Learning rate)：作为监督学习以及深度学习中重要的超参，其决定着目标函数能否收敛到局部最小值以及何时收敛到最小值。合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。

　　

收敛条件：

　　 误差小于某个预先设定的较小的值。

　　 两次迭代之间的权值变化已经很小。

　　设定最大迭代次数，当迭代超过最大次数就停止。