第二章
Tensorflow主要依赖两个工具:Protocol Buffer和Bazel Protocol. Protocol Buffer是一个结构数据序列化的的工具,在Tensorflow中大部分的数据都是通过Protocol Buffer的形式储存,Bazel是谷歌开源的编译工具。
第三章
-
3.1
- Tensor: 张量,多维数组。零阶张量表示标量,一阶张量表示向量...
- Flow: 计算图
tf.get_default_graph()获取当前默认计算图,通过tf.Graph.device()指定运行计算的设备。
-
3.2
- 一个张量保留了三个属性:
name、shape、type - 张量的作用:保留对中间结果的引用;计算图构造完成后,可以利用张量获得计算结果,如
tf.Session().run(result)(其中result为张量)
- 一个张量保留了三个属性:
-
3.3
-
会话Session用于管理Tensorflow的所有资源,执行定义的计算。Session不会默认生成,必须手动指定,当默认会话指定后,可以通过
<tf.Tensor>.eval()计算一个张量的取值。 -
tf.InteractiveSession()用于交互环境中,省去将产生会话注册为默认会话的过程,示例:sess=tf.InteractiveSession() print(result.eval()) # result为张量 sess.close() -
可以通过
ConfigProtocol Buffer配置生成的会话,示例:config=tf.ConfigProto(allow_soft_placement=True, log_device_placement=True) sess=tf.Session(config=config)另外,
ConfigProto可以配置类似并行线程数,GPU分配策略等。
-
-
3.4
- 神经网络的优化过程就是优化神经网络参数取值的过程;全连接神经网络是指相邻两层之间任何两个节点之间都有连接,也即多层感知机(MLP)。
- 前向传播过程:
tf.matmul(x,w)tf.random_normal()正态分布tf.truncated_normal()剪裁的正态分布,当随机出的值偏离超过两个标准差,将被重新随机。
第四章
-
4.1
线性模型的最大特点是任意线性模型的组合仍然是线性模型,而深度模型强调非线性。在线性可分问题中,线性模型就可以很好解决。因此深度模型的定义特意强调tea的目的是解决更为复杂的问题,所谓复杂问题至少是无法通过直线(或者高维空间中的平面)划分的。
-
4.2经典损失函数
-
分类:交叉熵(H(p,q)=-sum_xp(x)logq(x))越小,两个分布越接近
-
回归:均方误差(MSE(y,y')=frac{sum_{i=1}^n(y_i-y_i')^2}{n})
-
tf.clip_by_value()可以将一个张量的数值限制在一个区间之内,如tf.clip_by_value(v,2,4)将张量v中值小于2的替换为2,大于4的替换为4 -
tf.select(tf.greater(v1,v2),(v1-v2),(v2-v1))tf.greater()比较两张量大小,tf.select()根据bool值选择需要返回的张量,上例中,若v1>v2返回True,则返回(v1-v2)
-
-
4.3神经网络的优化过程
- 前向传播获得预测值,计算预测值和真实值的差距。
- 反向传播计算损失函数对每一个参数的梯度,再根据梯度和学习率使用梯度下降法更新每一个参数。
梯度下降法保证取得局部最优解,不保证取得全局最优解,只有当损失函数为凸函数时,梯度下降法取得全局最优解。
-
4.4
-
学习率设置方法:指数衰减法,
tf.train.exponential_decay()函数实现指数衰减学习率:decay_learning_rate=learning_rate*decay_rate^(global_step/decay_steps)其中,
learning_rate为初始学习率,decay_rate为衰减系数,global_step为当前总步数,decay_steps为衰减速度。当tf.train.exponential_decay()函数中的staircase参数设置为True时,成阶梯状衰减学习率。 -
过拟合:L1/L2正则化
L1正则化会让参数更稀疏,而L2不会。这是因为L2正则化中,当参数很小时,该参数的平方基本可以忽略,因此模型不会进一步把该参数调整为0。另一方面,L2正则化的计算公式可导,而L1正则化不可导,在优化过程中由于需要计算损失函数的偏导数,因此对含有L2正则化损失函数的优化更为简洁。
-
平滑滑动模型
Tensorflow中提供了
tf.train.ExponentialMovingAverage()来实现滑动平滑模型,其需要提供一个衰减率decay,这个衰减率用于控制模型的更新速度。ExponentialMovingAverage对每个变量都维护一个影子变量,该影子变量的初始值就是相应变量的初始值,而每次运行变量更新时,影子变量会更新为:shadow_variable=decay*shadow_variable+(1-decay)*shadow_variable其中,
shadow_variable为影子变量,variable为待更新变量,decay为衰减率。decay决定了模型的更新速度,decay越大,模型越稳定。
-
第五章
-
5.2
为了评测神经网络模型在不同参数下的效果,一般会从训练数据中抽取一部分作为验证数据。选取的验证数据越接近测试数据分布,模型在验证数据上的表现越可以代表在测试数据上的表现。
可以这样理解,验证数据是从训练集中抽取的,而测试数据完全是未见的。调整神经网络的结构如有无隐藏层或激活函数对最终的正确率影响较大;相比于滑动平均模型和指数衰减学习率,加入正则化的损失函数给模型带来的提升更为明显。
-
5.3
Tensorflow提供了通过变量名称创建或获取一个变量的规则,主要是通过
tf.get_variable()和tf.variable_scope()实现的。-
tf.Variable()创建一个变量,变量名称可选。 -
tf.get_variable()创建或获取一个变量,变量名称必填。
tf.get_variable()首先会试图创建一个参数,若创建失败(如已有同名参数),程序会报错以避免无意识的参数复用。如果需要通过tf.get_variable()获取一个已创建的变量,需要通过tf.variable_scope()函数生成一个上下文管理器,并明确指定reuse=True以获取已生成的变量。-
tf.variable_scope()函数可以控制tf.get_variable()函数的语义,当tf.variable_scope()使用参数reuse=True生成上下文管理器时,这个上下文管理器内所有的tf.get_variable()函数会直接获取已创建的变量,若变量不存在,则tf.get_variable()函数将报错;相反,若tf.variable_scope()函数使用参数reuse=None或reuse=False创建上下文管理器,tf.get_variable()将创建新变量。with tf.variable_scope('foo',reuse=True): v=tf.get_variable('v',shape=[1])tf.variable_scope()函数生成的上下文管理器也会创建一个Tensorflow中的命名空间,在命名空间内创建的变量都会带上这个命名空间名称作为前缀。v=tf.get_variable('v',shape=[1]) print(v.name) # 输出v:0,其中,"v"为变量名称,":0"表示这是生成变量这个运算的第一个结果 with tf.variable_scope('foo'): with tf.variable_scope('bar'): v2=tf.get_variable('v',shape=[1]) print(v2.name) # 输出"foo/bar/v:0",命名空间可以嵌套,同时变量名称也会加入 # 所有命名空间的名称作为前缀 with tf.variable_scope('',reuse=True): v3=tf.get_variable('foo/bar/v',shape=[1]) # 可以直接通过带命名空间名称的变量 # 名来获取其它命名空间下的变量
-
-
-
5.4
保存模型
# 定义计算图... saver=tf.train.Saver() with tf.Session() as sess: ... saver.save(sess,'path/model.ckpt')还原模型
# 定义计算图... saver=tf.train.Saver() with tf.Session() as sess: saver.restore(sess,'path/model.ckpt') # 加载已经训练好的参数保存和还原模型唯一不同的是,在加载模型的代码中没有参数初始化过程,而是将变量的值直接从文件中加载进来。
如果不想重复定义计算图,也可以直接加载已经持久化的图:
saver=tf.train.import_meta_graph('path/model.ckpt.meta') with tf.Session() as sess: saver.restore(sess,'path.model.ckpt') # 通过变量名获取张量 print(sess.run(tf.get_default_graph().get_tensor_by_name('add:0')))Tensorflow可以通过字典将模型保存时的变量名和需要加载的变量名联系起来。
- .ckpt.meta: 计算图结构
- .ckpt: 变量的值
- checkpoint: 该目录下所有的模型列表
-
6.2
卷积神经网络主要解决了全连接神经网络参数过多的问题,参数过多除了导致计算速度减慢,而且会引起过拟合问题。
卷积神经网络的组成:
-
输入层:图像 -> 三阶张量,张量的长宽表示图像的大小,深度代表了图像的色彩通道,如黑白图片的深度为1,RGB色彩模式下,图像的深度为3.
-
卷积层:卷积层将神经网络中的每一块进行更加深入的分析,从而得到抽象程度更高的特征,会改变节点矩阵的深度。
-
池化层:池化层不会改变张量的深度,但会缩小张量的大小,通过池化能够进一步缩小神经网络的参数。
-
全连接层:卷积层和池化层是自动图像特征提取,在特征提取完成之后,仍需要使用全连接层完成分类任务。
-
softmax层
处理后结果矩阵大小:
- 全0填充:(lceil in/stride ceil)
- 不使用全0填充:(lceil (in-filter+1)/stride ceil)
卷积层的参数个数和图像大小无关,它只和卷积核的尺寸、深度以及当前层节点矩阵的深度有关
卷积层示例:
filter_weight=tf.get_variable('weight',shape=[5,5,3,16],initializer=tf.truncated_normal_initializer(stddev=0.1)) # 卷积层权重变 # 量,前2个维度表示卷积层尺寸,第3个维度表示当前层深度,第4个维度表示卷积核维度 # 和卷积核参数一样,卷积核的偏置值也是共享的,16是卷积核深度,也即是下一个节点矩阵深度 biases=tf.get_variable('biases',shape=[16],initializer=tf.constant_initializer(1.)) # 卷积层前向传播算法:tf.nn.conv2d,第一个参数为当前层的节点矩阵,shape= # [batch_size,width,height,channel] # 第二个参数为上述卷积核权重;第三个参数提供长度为4的数组,第一维和最后一维一定是1,其余2个是长和 # 宽;第四个参数是填充方式,'SAME'(全0填充) / 'VALID'(不填充) conv=tf.nn.conv2d(input,filter_weight,stride=[1,1,1,1],padding='SAME') # tf.nn.bias_add()为每一个卷积核加上偏置项,不可直接用加法,因为需要向矩阵上不同位置的卷积核加上 # 同样的偏置量 bias=tf.nn.bias_add(conv,biases) # ReLU,去线性化 actived_conv=tf.nn.relu(bias)卷积层和池化层中过滤器移动的方式是相似的,唯一区别在于池化层使用的过滤器是横跨整个深度的,而卷积层使用的过滤器仅仅影响一个深度上的节点。
卷积:
matmul([width,height,channel],[width,height,channel,new_channel]) # 当前层 # feature_map × 当前卷积层参数池化层不仅要在长宽两个维度上移动,而且要在深度这个维度上移动。
# 池化层: tf.nn.max_pool(),第一个参数是当前层的节点矩阵,shape=[batch_size, width, # height, channel] # 第二个参数为过滤器尺寸,4维数组,第1和第4维必须为1;第三个参数为步长,4维数组,第1和第4维必须为 # 1;第四个参数为填充方式 pool=tf.nn.max_pool(actived_conv,ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME')另外还有
tf.nn.avg_pool平均池化层 -
-
6.4LeNet-5
-
layer1: 卷积层
-
输入层大小:32×32×1
-
conv1: 5×5, depth: 6, VALID, stride=1
输出:
[lceil (32-5+1)/1 ceil =28\ depth=6 ]参数数量:
[5 imes 5 imes 1 imes 6+6=156(+6是偏置值参数数量) ]下一层节点矩阵有28×28×6个节点,每个节点有5×5个连接与当前层连接,故本层有(28×28×6)×(5×5+1)个连接
-
-
layer2: 池化层
-
layer3: 卷积层
-
layer4: 池化层
-
layer5: 全连接层
- 输出节点个数120,共5×5×16×120+120个参数
-
layer6: 全连接层
-
layer7: 全连接层
另外,dropout只在训练过程中使用
卷积神经网络结构:输入层 -> (卷积层+池化层?) + 全连接层 + ...
池化层可以起到防过拟合的作用,但有些论文发现也可以直接通过调整卷积层步长来完成;在过滤器深度上,大部分卷积神经网络都采用逐层递增的方式。
Inception-v3
LeNet-5模型中,不同卷积层通过串联连接在一起,然而在Inception-v3中的Inception结构是将不同卷积层通过并联连接在一起。
Inception模块:
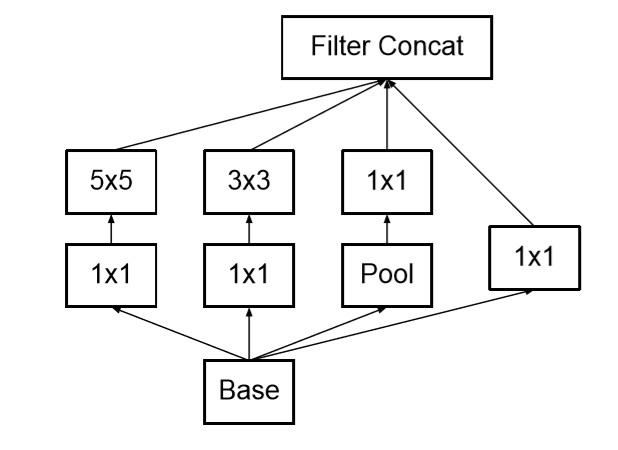
过滤器大小不同,但所有过滤器都采用全0填充且步长为1,则前向传播得到的结果矩阵的长和宽都和输入矩阵一致,则不同滤波器的结果矩阵都可以拼接成一个更深的矩阵。
上述一个卷积层在Tensorflow中只需要5行代码,可以使用Tensorflow slim减少代码量:
# 直接使用Tensorflow原始API实现卷积层 with tf.variable_scope(scope_name): weights=tf.get_variable('weight',...) biases=tf.get_Variable('biases',...) conv=tf.nn.conv2d(...) relu=tf.nn.relu(tf.nn.bias_add(conv,biases))# 使用Tensorflow slim实现卷积层,slim.conv2d中第一个参数为输入节点矩阵,第二个参数为卷积层过滤 # 器深度,第三个参数为过滤器尺寸,可选参数还有步长、是否全0填充等 net=slim.conv2d(input,32,[3,3]) -
-
6.5迁移学习
将一个数据集上训练好的模型快速迁移到另一个数据集上。根据论文DeCAF,可以保留训练好的Inception-v3模型中所有卷积层的参数,只是替换它最后一层全连接层,在这最后一层之前的网络层被称作瓶颈层(bottleneck)。瓶颈层可以看作是对图像进行特征提取的过程,瓶颈层输出的节点向量可以看作是图像一个精简且表达能力更强的特征向量。
一般而言,数据量足够情况下,迁移学习的效果不如完全重新训练,但是迁移学习所需要的时间和样本量都远远小于训练完整的模型。
第七章
Tensorflow提供了一种统一的格式来存储数据,这个格式就是TFRecord,TFRecord格式可以统一不同的原始数据格式,并更加有效的管理不同的属性。
TFRecord文件中的数据都是通过tf.train.ExampleProtocol Buffer的格式存储的。tf.train.Example中包含了一个属性名称到取值的字典,其中属性名称为一个字符串,属性的取值可以为字符串(BytesList)、实数列表(FloatList)和整数列表(Int64List)
TFRecord示例:
'''
转为TFRecord格式
'''
def _int64_feature(value):
return tf.train.Feature(int64_list=tf.train.Int64List(value=[value]))
def _bytes_feature(value):
return tf.train.Feature(byte_list=tf.train.BytesList(value=[value]))
writer=tf.python_io.TFRecordWriter('path/output.tfrecords')
for index in range(num_examples):
# 将图像转换为二进制字符串
image_raw=image[index].tostring()
# 将一个样例转为Example Protocol Buffer,并将所有信息都写入这个数据结构中
example=tf.train.Example(features=tf.train.Features(features={
'pixel':_int64_feature(pixels),
'label':_int64_feature(np.argmax(labels[index])),
'image_raw':_byte_feature(image_raw)
}))
# 将一个Example写入TFRecord文件
writer.write(example.SerializeToString())
writer.close()
'''
读取TFRecord文件
'''
reader=tf.TFRecordReader()
# 使用tf.train.string_input_producer()函数创建一个队列来维护输入文件列表
filename_queue=tf.train.string_input_producer(['path/output.tfrecords'])
# 从文件中读取一个样例,若希望读取多个,使用read_up_to()函数
_,serialized_example=reader.read(filename_queue)
# Tensorflow提供两种不同的属性解析方法,一种是tf.FixLenFeature,这种方法解析的结果为一个Tensor
# 另一种是tf.VarLenFeature,这种方法解析的结果是SparseTensor,用于处理稀疏数据
# 注意:解析数据的格式应与写入数据格式一致
features=tf.parse_single_example(serialized_example,features={
'image_raw':tf.FixLenFeature([],tf.string),
'pixels':tf.FixLenFeature([],tf.int64),
'label':tf.FixLenFeature([],tf.int64),
})
# tf.decode_raw()可以将字符串解析成图像对应的像素数组
images=tf.decode_raw(features['image_raw'],tf.unit8)
labels=tf.cast(features['label'],tf.int32)
pixels=tf.cast(features['pixels'],tf.int32)
sess=tf.Session()
# 启动多线程处理数据
coord=tf.train.Coordinator()
threads=tf.train.start_queue_runners(sess=sess,coord=coord)
image,label,pixel=sess.run([images,labels,pixels])
第八章
-
8.1
循环神经网络的主要用途是处理和预测序列数据,之前的全连接网络或卷积神经网络中,层与层之间是全连接或部分连接的,但每层之间是无连接的,而循环神经网络在一个隐藏层之间的节点是有连接的,隐藏层的输入不仅包含输入层的输入,还包括上一时刻隐层的输出。
循环神经网络中,将上一时间步的状态与当前时间步的输入拼接成一个大的向量作为循环体当前时间步的输入,为了将当前时间步的状态转化为最后的输出,循环神经网络还需要另外一个全连接神经网络来完成这一过程。

-
8.2解决序列长程依赖(梯度消失):LSTM长短时记忆网络
LSTM是一种拥有三个门的特殊网络结构
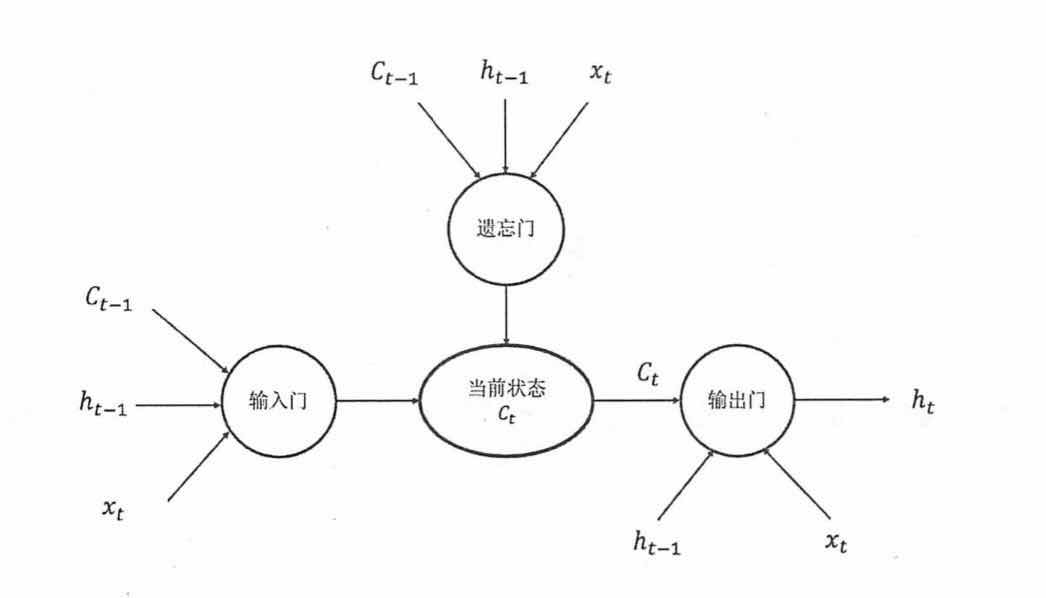
上图中,(C_{t-1})为上一时间步的状态,(h_{t-1})为上一时间步的输出,(x_t)为当前时间步的输入
门:使用sigmoid作为激活函数输出0~1之间的数值,描述当前有多少信息可以通过这一结构。
- 遗忘门:使神经网络“忘记”无用的信息
- 输入门:使神经网络“补充”最新信息
- 输出门:根据新得到的状态产生当前时间步的输出
''' Tensorflow中实现LSTM前向传播 ''' # 定义LSTM结构 lstm=rnn_cell.BasicLSTMCell(lstm_hidden_size) # 生成全0初始状态 state=lstm.zero_state(batch_size,tf.float32) loss=0. # 理论上RNN可以处理任意长度的序列,但为了避免梯度消失的问题,会规定一个最大序列长度 # 在该例中,使用num_steps表示该最大序列长度 for i in range(num_steps): # 在第0时刻创建变量,之后时刻均复用该变量 if i>0: tf.get_variable_scope().reuse_variables() # 每一步处理序列中的一个时刻,将当前输入current_input和前一时间步上的状态state传入LSTM # 可以得到当前时间步上LSTM的输出lstm_output和更新后的状态state lstm_output,state=lstm(current_input,state) # 将当前时刻输出传入全连接层得到最终输出 final_output=fully_connected(lstm_output) # 计算当前时间步的损失 loss+=calc_loss(final_output,expected_output) # 优化算法降loss -
8.3
-
当前时间步的输出不仅仅和之前的状态有关,而且和之后的状态有关,则需要双向循环神经网络(Bidirectional RNN),双向循环神经网络是由两个循环神经网络上下叠加在一起组成的。在每个时刻t,输入会同时提供给这两个方向的循环神经网络,而输出则是由两个单向的循环神经网络共同决定的。
[s_t=f(Ux_t+Ws_{t-1}) \ s_t'=f(U'x_t+W's_{t+1}')\ o_t=g(Vs_t+V's_t') ]其中,(s_t)为前向LSTM输出,(s_t')反向LSTM输出,(U、W、U'、W'、V、V')为待训练参数,(f、g)为激活函数,(x_t)为本时刻的输入。
-
为了增强模型表达能力,可以将每一时间步上的循环体重复多次,即深层循环神经网络(deepRNN),深度循环神经网络将循环体结构复制多次,每一层的循环体中参数是一致的,但不同层的参数可以不同。
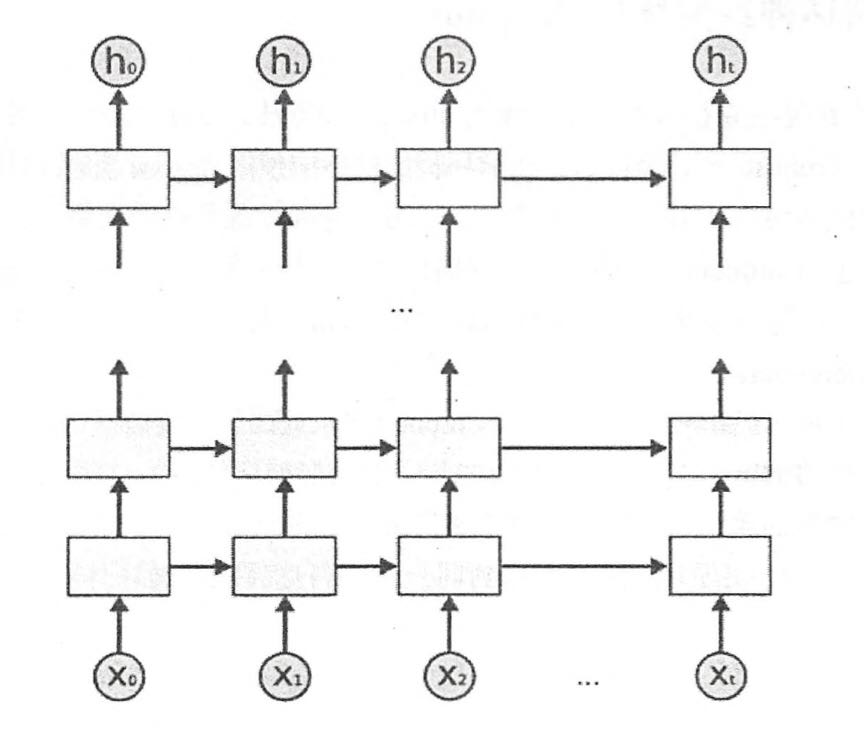
''' 深层循环神经网络 ''' # 定义基本LSTM结构作为循环体的基本结构,深度循环神经网络也支持其它循环体结构 lstm=rnn_cell.BasicLSTMCell(lstm_size) # 通过MultiRNNCell类实现深层循环神经网络的前向传播过程,其中number_of_layers表示深度循环神# 经网络的深度,即x_t经过多少个LSTM结构才可到达h_t stacked_lstm=rnn_cell.MultiRNNCell([lstm]*number_of_layers) # 获取初始状态 state=stacked_lstm.zero_state(batch_size,tf.float32) # 计算每一时刻的前向传播结果 for i in range(len(num_steps)): if i>0: tf.get_variable_scope().reuse_variables() stack_lstm_output,state=stacked_lstm(current_input,state) final_output=fully_connected(statck_lstm_output) loss+=calc_loss(final_output,expected_output)循环神经网络只在不同层之间使用dropout,而同一层内各时间步内不适用dropout。事实上,大多数循环神经网络的图示都是按时间展开后的结果,实际上只是一个单元。
lstm=rnn_cell.BasicLSTMCell(lstm_size) # 使用DropoutWrapper类来实现dropout功能,该类通过两个参数控制dropout # 一个参数是input_keep_prob,用来控制输入dropout概率,另一个参数是output_keep_prob用来控# 制输出dropout概率 dropout_lstm=tf.nn.rnn_cell.DropoutWrapper(lstm,output_keep_prob=0.9) # 使用了dropout的LSTM基础上定义MultiRNN stacked_lstm=rnn_cell.MultiRNNCell([dropout_lstm]*number_of_layers)n-gram, 有限历史假设:当前单词出现概率仅仅与前面的n-1个单词相关,即:
[p(s)=p(w_1,w_2,...,w_m)=prod _i^mp(w_{i-n+1},...,w_{i-1}) ]n-gram中的n表示当前单词依赖的前面单词的个数,通常n取1、2、3.理论上n越大,模型越精确,也越复杂。若某种语言的单词表大小为k,则n-gram模型需要估计的不同参数数量为(k^n).n-gram模型的参数一般采用最大似然估计(MLE):
[p(w_i|w_{i-n+1},...,w_{i-1})=frac{C(w_{i-n+1},...,w_{i-1},w_i)}{C(w_{i-n+1},...,w_{i-1})} ]其中,(C(x))表示序列X中在训练语料中出现的次数。
-
第九章
-
9.2
tf.variable_scope()函数和tf.name_scope()函数都提供了命名空间的功能。在TensorBoard中,同一命名空间下的所有节点会缩略成一个节点。tf.name_scope()和tf.variable_scope()大部分等价。''' 将当前计算图输出到TensorBoard日志文件 ''' writer=tf.train.SummaryWriter('path/log',tf.get_default_graph()) writer.close()GRAPHS栏下,选择右侧的session runs任意步数,Color栏中会多出Compute Time和Memory选项,可利用其查看神经网络个计算步骤上的计算用时和内存占用。TB栏名 备注 tf.scalar_summary EVENTS 标量监控数据 tf.image_summary IMAGES tf.audio_summary AUDIO tf.histogram_summary HISTOGRAMS 张量监控数据,记录张量取值分布 ''' 生成变量监控信息,并定义生成监控信息日志的操作,其中var给出了需要记录的张量,name给出了在可视化结果中显示的图表名称,该名称一般和变量名一致 ''' def variable_summaries(var,name): # 将生成监控信息的操作放在同一命名空间下 with tf.name_scope('summary'): # 通过tf.histogram_summary()函数记录张量中的取值分布,对于给定的图表名称和张量, # tf.histogram_summary会生成一个Summary Protocol Buffer,和Tensorflow其它 # 操作类似,tf.histogram_summary()不会立即执行,只有当sess.run()明确调用该操作时, # 才会真正执行。 tf.histogram_summary(name,var) # 计算变量的平均值和方差,并定义生成平均值和方差信息日志的操作,相同命名空间下的监控指标会 # 整合到一栏中。 mean=tf.reduce_mean(var) tf.scalar_summary('mean/'+name,mean) stddev=tf.sqrt(tf.reduce_mean(tf.square(var-mean))) tf.scalar_summary('std/'+name,stddev) # 输入向量还原为图像的像素矩阵,并通过tf.image_summary()函数定义将当前的图片信息写入日 # 志 with tf.name_scope('input_shape'): image_shaped_input=tf.reshape(x,[-1,28,28,1]) tf.image_summary('input',image_shaped_input) # 由于写日志操作过多,Tensorflow提供了tf.merge_all_summary()来整合所有写日志操作 # 从而使得所有日志生成操作执行一次,所有日志即可写入文件 merged=tf.merge_all_summaries() with tf.Session() as sess: summary_writer=tf.train.SummaryWriter('path/log',sess.graph) for i in range(TRAIN_STEPS): ... summary,_=sess.run([merged,train_op],feed_dict={}) # 所有日志写入文件,使TensorBoard拿到本次运行信息 summary_writer.add_summary(sumamry,i) summary_writer.close()
第十章
-
10.1
默认情况下,即使机器有多个CPU,Tensorflow也不会区分它们,所有的CPU都使用"/cpu:0"作为名称,而一台机器上的不同GPU的名称是不同的,第n个GPU在Tensorflow这种的名称为"gpu:n",可以通过
log_device_placement来输出执行每一行运算的设备。可以通过tf.device()手工指定运算设备。
with tf.device('/gpu:1'):
c=a+b
`allow_soft_placement=True`允许当运算无法在GPU上执行时,在CPU上执行。
```python
sess=tf.Session(config=tf.ConfigProto(allow_soft_placement=True,
log_device_placement=True))
-
10.2
常见的并行化深度学习模型有同步模式和异步模式。
-
异步模式时单机模式复制多份,每一份使用不同的训练数据进行训练,各自“独立”地更新参数,在异步模式下,不同设备之间完全独立,异步模式可能无法达到较优的训练结果。
-
同步模式下,所有设备同时读取参数取值,并且当反向传播算法完成之后协同同步更新参数,单个设备需要等待所有设备都完成反向传播之后,再统一更新参数(取参数更新平均值等方式更新参数)。同步模式效率低于异步模式。
opt=tf.train.GradientDescentOptimizer(learning_rate) # 计算SGD梯度 grads=opt.compute_gradients(cur_loss) # 使用梯度更新参数 apply_gradient_op=opt.apply_gradients(grads,global_step=global_step) -
-
10.4
运行反向传播的机器是一个任务(task),而所有运行方向传播的机器则被称作工作(work)。一个工作专门负责存储,获取及更新变量取值,这个工作所包含任务统称为参数服务器。另一个工作专门运行反向传播算法来获取参数梯度,这一工作称作计算服务器。
- 计算图内分布式:各任务共用计算图的参数,只分发计算部分
- 计算图间分布式:各任务参数独立,共同参数放到同一参数服务器上
参考文献
本文是Tensorflow 实战Google深度学习框架的读书笔记。淘宝链接:Tensorflow实战Google深度学习框架