上节学习笔记主要学了点二分类(Binary Classification)链接如右边https://www.cnblogs.com/mengmengxia/p/10534960.html 这篇主要学习逻辑回归、逻辑回归的代价函数和梯度下降法。那么先看如何使用逻辑回归来解决二分类问题。
- 逻辑回归(Logistic Regression)
逻辑回归就是这样的一个过程:面对一个回归或者分类问题,建立代价函数,然后通过优化方法迭代求解出最优的模型参数,然后测试验证我们这个求解的模型的好坏。Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别)回归模型中,y是一个定性变量,比如y=0或1,logistic方法主要应用于研究某些事件发生的概率。
逻辑回归中$widehat{p}$=P(y=1|x)表示为1的概率,取值范围在[0,1]之间。使用线性模型,引入参数w和b,权重w的维度是(nx,1),b是一个常数项。则可以把逻辑回归的线性预测输出写成:$widehat{y}$=wTx +b。
在逻辑回归中$widehat{y}$应该在0到1之间,但wTx +b 可能比1要大的多,或者甚至为一个负值。所以为了使$widehat{y}$的取值在0到1之间,方法是引入Sigmoid 函数。则逻辑回归的预测输出可以完整写成:$widehat{y}$=Sigmoid(wTx +b)=δ(wTx +b)
既然上面提到了Sigmoid 函数,我就在普及一下关于此函数的知识:
Sigmoid函数是一个在生物学中常见的S型函数,也成为S型生长曲线。Sigmoid函数是一个良好的阈值函数,其性质是连续、光滑、严格单调、关于(0、0.5)中心对称。Sigmiod函数常被用作神经网络的阈值函数,将变量映射到0、1之间。
Sigmoid函数由下列公式定义:S(x)=$frac{1}{1+e^{-x}}$ 其图像如下图1所示:
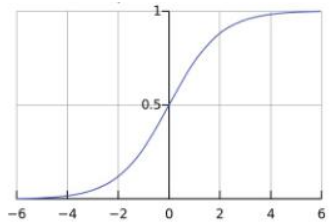
从图1的Sigmoid函数曲线可以看出,当x值很大时,函数值趋向于1;当x值很小时,函数值趋向于0。且当x=0时,函数值为0.5。值得注意的是其对x 的导数可以用自身表示:S'(x)=$frac{e^{-x}}{left ( 1+e^{-x} ight )^{2}}$ =S(x)(1-S(x))
下个笔记我们学习逻辑回归的代价函数,让我们一起来学习,共同进步吧!!