參考:http://www.cnblogs.com/chanme/p/3843859.html
然后我看到在别人的AC的方法里还有这么一种神方法,他预先设定了一个阈值K,当当前的更新操作数j<K的时候,它就用一个类似于树状数组段更的方法,用一个 d数组去存内容,譬如它要在区间 [3,6]上加一段fibonacci
原来:
id 0 1 2 3 4 5 6 7 8 9 10
d 0 0 0 0 0 0 0 0 0 0 0
更新:
id 0 1 2 3 4 5 6 7 8 9 10
d 0 0 0 1 0 0 0 -5 -3 0 0
我们能够发现,当利用 d[i]=d[i]+d[i-1]+d[i-2] i由小到大更新后就会得到
id 0 1 2 3 4 5 6 7 8 9 10
d 0 0 0 1 1 2 3 0 0 0 0
所以对于[L,R]上加一段操作,我们能够d[L]+=1; d[R+1]-=f[R-L+2],d[R+2]=f[R-L+1];
所以假如我更新了m次,我每次更新的复杂度是O(1),我把全部数求出来一次的复杂度是O(n)
然后他的算法是这种,j<K的时候更新的时候依照上述方法更新,询问的话则是将询问区间和更新的区间求交,把交的和加上去。
当j==K的时候,利用d还原出新的a,把当前的区间清0.
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=330000;
const long long int mod=1000000009LL;
typedef long long int LL;
int n,m,k;
LL a[maxn],sum[maxn],fib[maxn],gib[maxn];
LL d[maxn]; int L[1100],R[1100];
void init()
{
fib[1]=1LL,fib[2]=1LL;
gib[1]=1LL,gib[2]=2LL;
for(int i=3;i<=n+50;i++)
{
fib[i]=(fib[i-1]+fib[i-2])%mod;
gib[i]=(gib[i-1]+fib[i])%mod;
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%I64d",a+i);
sum[i]=sum[i-1]+a[i];
}
init();
while(m--)
{
int c,l,r;
scanf("%d%d%d",&c,&l,&r);
if(c==1)
{
L[k]=l,R[k]=r; k++;
d[l]=(d[l]+1LL)%mod;
d[r+1]=(d[r+1]-fib[r-l+2]+mod)%mod;
d[r+2]=(d[r+2]-fib[r-l+1]+mod)%mod;
if(k>=1000)
{
for(int i=1;i<=n;i++)
{
if(i>=2)
d[i]=((d[i]+d[i-1])%mod+d[i-2])%mod;
a[i]=(a[i]+d[i])%mod;
sum[i]=sum[i-1]+a[i];
}
memset(d,0,sizeof(d)); k=0;
}
}
else if(c==2)
{
LL ret=0;
for(int i=0;i<k;i++)
{
int _left=max(l,L[i]);
int _right=min(r,R[i]);
if(_left>_right) continue;
int s=_left-L[i]+1,e=_right-L[i]+1;
ret=((ret+gib[e])%mod-gib[s-1]+mod)%mod;
}
ret=((ret+sum[r])%mod-sum[l-1]+mod)%mod;
printf("%I64d
",(ret+mod)%mod);
}
}
return 0;
}
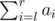 modulo
modulo