Logistic Regression 逻辑回归
1.模型
逻辑回归解决的是分类问题,并且是二元分类问题(binary classification),y只有0,1两个取值。对于分类问题使用线性回归不行,因为直线无法将样本正确分类。
1.1 Sigmoid Function
因为 y∈{0,1},我们也希望 hθ(x)∈{0,1}。第一种选择是 logistic函数或S型函数(logistic function/sigmoid function)。g(z)值的范围在0-1之间,在z=0时为0.5,z无穷小g(z)趋近0,z无穷大g(z)趋近1。
其公式为:
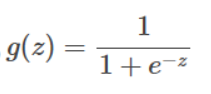
图像为:

同时g(z)的倒数有以下这个特性,即g(z)的倒数刚好等于 g(z)(1-g(z)):
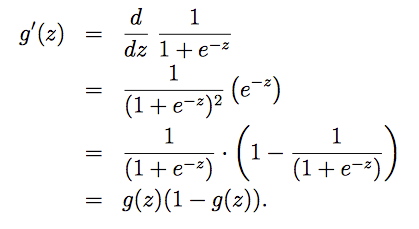
假设 hθ(x) 的公式为:
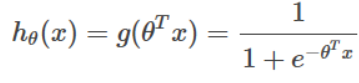
1.2 threshold function
logistic函数是曲线,如果想更加明确地将输出分为0、1两类,就要用到阶梯函数/临界函 (threshold function)。很简单直白的定义:
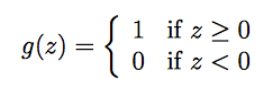
如果使用threshold函数替换logistic函数,则算法称为感知学习算法(Perceptron learning algorithm)。
2.策略
下面根据逻辑回归模型,调整 θ 对其进行拟合。首先进行以下假设:
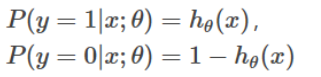
两个式子可以改写成一个式子:![]()
逻辑回归使用的策略是最大化对数似然函数。似然函数 likelihood function 与对数似然函数分别为:

注:似然函数,就是计算整个训练集中每组 x,y 成立的可能性,即将每一组 x(i),y(i) 发生的概率相乘。
求对数是为了计算方便
3.算法
逻辑回归的目的是使可能性最大,即 maximizing 最大化似然函数的值。(线性回归是为了使代价最小,即minimizing代价函数的值,求最低点)
3.1 gradient ascent 梯度上升
先假设只有一个训练样本,对函数 l(θ) 求偏导可得:
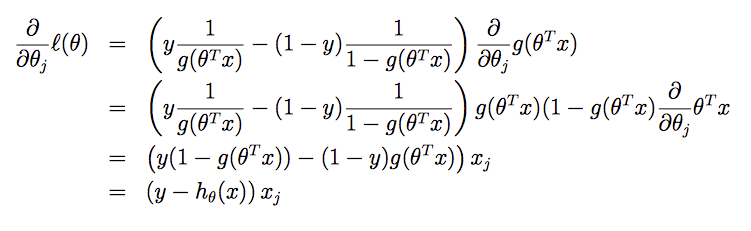
如果有多个样本,同样需要使用梯度算法。但和线性回归有一个区别:为了使函数最大化,要将之前更新算法中的 “-“ 改为“+“,“下降“改为“上升“。
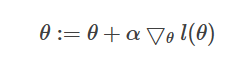
将上面单个训练样本J(θ)的导数进行向量化,得到 随机梯度上升算法 的更新原则(随机没有求和,批量有求和):![]()
这和上一讲中的最小二乘法更新规则的表达式一样,但是其中 hθ(x) 却不同。最小二乘法中的 hθ(x) 是线性函数,而此表达式中的 hθ(x) 是sigmoid函数。
3.2 Newton’s method 牛顿方法
极值点就是导数为0的地方,所以最大化对数似然函数的另一个求法是求对数似然函数导数为0的点。
(1)考虑最简单情况:θ是一个实数,首先找到一个实数域上的方程 f,f(θ)=0。 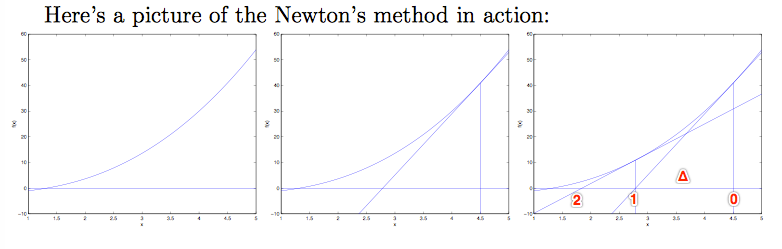
从起始点θ0开始,找到f(θ0)处的切线,与坐标轴相交于θ1。再从求 f(θ1) 处的切线,与坐标轴相交于θ2。不断迭代,直到切线斜率为0。
如果将 θ0 和 θ1 两点之间的距离记为Δ,可以通过求Δ来判断下一个θ在哪。根据 tan() 的特性,有:![]()
所以牛顿方法执行更新规则:

如果想要找到 θ 使得 l(θ) 最大,那么 θ 满足 l′(θ) = 0,可以将牛顿方法运用其中,将 l′(θ)替代上式中的 f(θ),得到:

注:如果想要使用牛顿方法最小化而不是最大化一个函数,公式怎么改?答案是不改,因为最小和最大值处对应的导数都是0。
(2)考虑一般化情况,θ 是一个向量。则一般化的牛顿方法(也称作Newton-Raphson method) 为: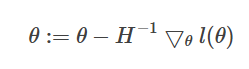
![]()
H表示黑塞矩阵(Hessian matrix),是二阶导数矩阵。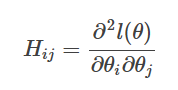
3.2 牛顿方法的优缺点
优点:牛顿方法比梯度上升算法减少了迭代次数,通常来说有更快的收敛速度,相对来说经过很少次迭代就能接近最小值。也称为二次收敛 quadratic conversions,即收敛速度几乎翻倍。
缺点:每次迭代都要重新计算 Hessian矩阵的逆,如果在大规模数据中涉及很多特征,将花费巨大计算代价并且变慢。
Google 是利用逻辑回归预测搜索广告的点击率。
https://blog.csdn.net/TRillionZxY1/article/details/77099955