【原】Coursera—Andrew Ng机器学习—编程作业 Programming Exercise 1 线性回归

作业说明

　　Exercise 1，Week 2，使用Octave实现线性回归模型。数据集  ex1data1.txt ，ex1data2.txt

　　单变量线性回归必须实现，实现代价函数计算Computing Cost 和 梯度下降Gradient Descent。

　　多变量线性回归可选，实现 特征Feature Normalization、代价函数计算Computing Cost 、 梯度下降Gradient Descent  和 Normal Equations 。

文件清单

• ex1.m
• ex1_multi.m
• ex1data1.txt - ex1.m 用到的数据组
• ex1data2.txt - ex1_multi.m 用到的数据组
• submit.m - 提交代码
• [*] warmUpExercise.m
• [*] plotData.m
• [*] computeCost.m
• [*] gradientDescent.m
• [+] computeCostMulti.m
• [+] gradientDescentMulti.m
• [+] featureNormalize.m
• [+] normalEqn.m

　　* 为必须要完成的
　　+ 为可

　　背景：假设我们现在是个连锁餐厅的老板，已经在很多城市开了连锁店（提供训练组），现在想再开新店，需要通过以前的数据预测新开的店的收益。

　　ex1data1.txt 提供所需要的训练组，第一列是城市人口，第二列是对应的收益。负值代表着亏损。

结论

　　当数据的特征维度比较小的时候，使用正规方程方法不需要进行特征归一化，而且结果稳定。梯度下降有可能得到局部最优解，导致结果不同。

　　注意矩阵计算的一些问题，求和前面一项需要转置。

必做题  单变量线性回归

一、warmUp

 　　单变量线性回归入口在ex1.m

　　warmUpExercise.m

A = eye(5)

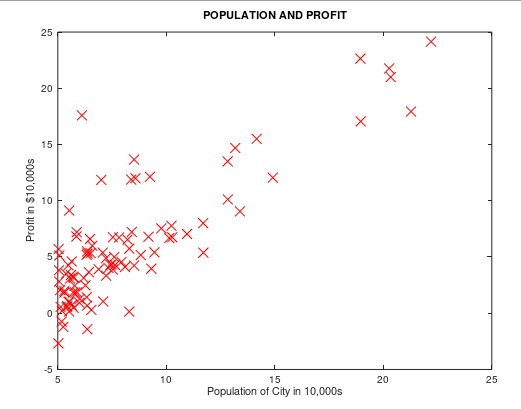
二、绘制数据图

　　我实现的 plotData.m：

  plot(x,y,'rx', 'MarkerSize', 10);
  xlabel('Population of City in 10,000s');
  ylabel('Profit in $10,000s');
  title('POPULATION AND PROFIT');

　　 ex1.m 中的调用：

%% ======================= Part 2: Plotting ======================= 3 data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
 8 plotData(X, y);

 　　运行效果如下：

 三、代价函数

　　我实现的 computeCost.m：

function J = computeCost(X, y, theta) 7 m = length(y); % number of training examples
10 J = 0;
17   predictions = X * theta; % predictions of hapothesis on all m examples
  sqrErrors = (predictions - y) .^ 2; % squared errors .^ 指的是对数据中每个元素平方
  
  J = 1 / (2 * m) * sum(sqrErrors); 
end

 四、梯度下降

　　我实现的 gradientDescent.m

　    矩阵性质：(AB)^T =B^TA^T

function [theta, J_history, theta_history] = gradientDescent(X, y, theta, alpha, num_iters) 7 m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
theta_history = zeros(2, num_iters); % 【改动】使用 2×iteration维矩阵，保存theta每次迭代的历史

for iter = 1:num_iters

    % 这里为了方便理解 拆的比较细，可以组合成一步操作 theta = theta - (alpha / m) * X' * (X * theta - y)
    % prediction h(x)  m×2矩阵 * 2×1向量 = m维列向量
    predictions = X * theta; 
    % error h(x)-y m维列向量
    errors = predictions - y; % 
    % derivative of J()  m维行向量 * m×2矩阵 = 2维列向量
    lineLope =  X' * errors;  
    % theta 2维列向量
    theta = theta - (alpha / m) * lineLope; %
    38     J_history(iter) = computeCost(X, y, theta);  % Save the cost J in every iteration 
    theta_history(:,iter) = theta;  % 给theta_history 第iter列赋值
end

end

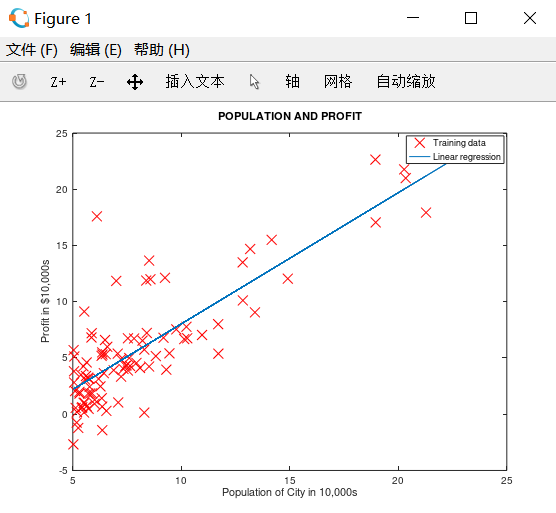
五、绘制预测曲线　　

　　ex1.m 中的调用：

%% =================== Part 3: Cost and Gradient descent ===================

% 设置 X 和 theta
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters

% 设置迭代次数和学习速率
iterations = 2000;
alpha = 0.01;
12 % compute and display initial cost      计算theta=[0;0]时代价
J = computeCost(X, y, theta);16 
% further testing of the cost function  计算theta=[-1;2]时代价
J = computeCost(X, y, [-1 ; 2]);21 
fprintf('
Running Gradient Descent ...
')27 % 【改动1】改为获取多个返回值，J_history保存每次迭代的代价，theta保存每次迭代的theta0和theta1
% 原：theta = gradientDescent(X, y, theta, alpha, iterations);
[theta,J_history,theta_history] = gradientDescent(X, y, theta, alpha, iterations);
36 
% Plot the linear fit 在数据图上绘制最终的拟合直线
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure

 　　运行结果如下：

 四、绘制cost和theta变化曲线

 自己加的功能。在ex1.m中增加以下代码，绘制图像。展示迭代过程中 cost 和 theta 的变化曲线

% --------------【改动2】绘制代价和theta变化曲线 start --------------
fprintf('Size of J_history saved by gradient descent:
');
fprintf('%f
', size(J_history));
iterX = [1:iterations]'; % 生成图像横坐标，迭代次数

% 绘左侧图，展示迭代过程中代价的变化曲线
subplot(1,2,1);
plot(iterX, J_history, '-','linewidth',3); % 绘制代价函数曲线
title('cost of each step'),
xlabel('iteration'),ylabel('value of cost'),
legend('value of cost');

% 绘右侧图，展示迭代过程中theta的变化曲线
theta0_history = theta_history(1,:);
theta1_history = theta_history(2,:);
subplot(1,2,2);
plot(iterX,theta0_history,'-','linewidth',2);
hold on;
plot(iterX,theta1_history,'-','linewidth',2,'color','r');
title('theta of each step'),xlabel('iteration'),ylabel('value of theta'),legend('theta0','theta1');
% --------------【改动2】绘制代价和theta变化曲线 end --------------

% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] * theta;
fprintf('For population = 35,000, we predict a profit of %f
',...
    predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f
',...
    predict2*10000);

输出如下：

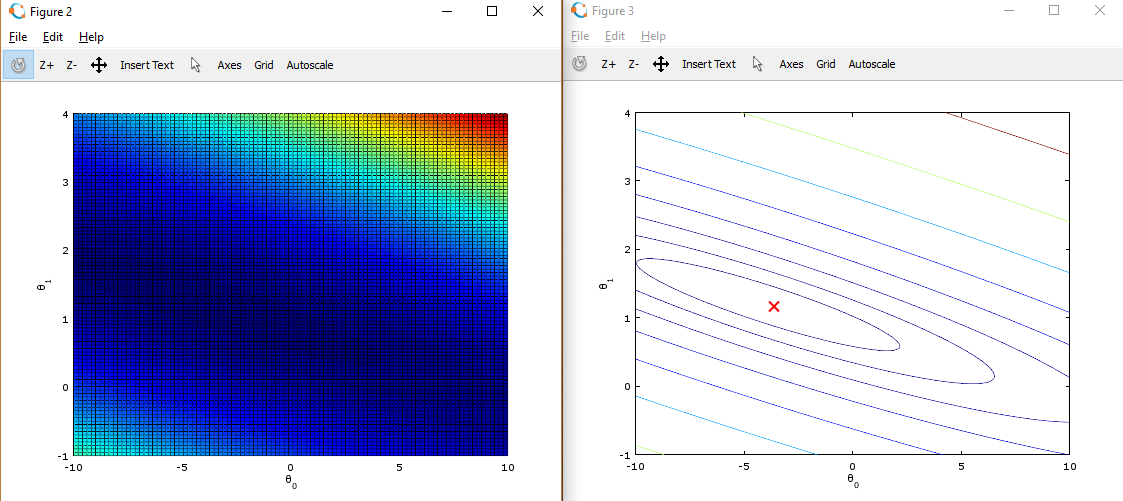
五、绘制代价函数三维曲线 和 等高线图

　　ex1.m 调用：

　　1、初始化 theta0 为（-10，10）均分100个点，theta1 为（-1,4）均分100个点，J_vals 为100 * 100的数组

　　这里使用了Matlab中的均分计算指令 linspace(x1,x2,N) ，用于产生x1、x2之间的N点行线性的矢量。其中x1、x2、N分别为起始值、终止值、元素个数。默认N为100。 

　　2、循环计算每组（theta0，theta1），用 J_vals 保存对应的代价cost。

%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...
')

% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);

% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));

% Fill out J_vals
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
      t = [theta0_vals(i); theta1_vals(j)];
      J_vals(i,j) = computeCost(X, y, t);
    end
end


% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('	heta_0'); ylabel('	heta_1');

% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('	heta_0'); ylabel('	heta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

　　3、将theta0作为X坐标，theta1作为Y坐标，J_vals作为Z坐标，绘制三维图形

　　4、将theta0作为X坐标，theta1作为Y坐标，绘制J_vals的等高线图

　　5、在等高线图中，标记上面求出的使代价函数最小的 theta0，theta1点的位置。在等高线中心

 

　　这些图像的目的是为了展示 随着Θ₀ 和 Θ₁ 的改变，J值的变化。（在2D轮廓图中比3D的更直观）。最小点是Θ₀ 和 Θ₁最适点， 每一步梯度下降都会更靠近这个点。

可以通过旋转看到为什么叫“轮廓图”：

---

 选做 多变量线性回归

 一 、特征归一化

需要用特性放缩让数据的范围缩小，使得梯度下降计算的更快：

• • 计算每个特性的平均值(mean)
  • 计算标准差(standard deviations)
  • 特性放缩(feature scaling)

* 这里利用的是标准差(standard deviation)，也可以使用差值(max - min)。

 　　featureNormalize.m 如下：

 1 function [X_norm, mu, sigma] = featureNormalize(X)
 7 
 9 X_norm = X;
10 mu = zeros(1, size(X, 2)); % 1行，列数和X相同
11 sigma = zeros(1, size(X, 2));
12 
13 % ====================== YOUR CODE HERE ======================
29 mu = mean(X);
30 sigma = std(X);
32 X_norm = (X_norm - mu) ./ sigma;
35 
36 end

二、代价函数和梯度下降

 　　因为在单变量线性回归中，使用的是向量化的计算方法，对于多变量线性回归同样适用。不需要重新写

　　 computeCostMulti.m 和 computCost.m 一样，gradientDescentMulti.m 和gradientDescent.m 一样

　　ex1_multi.m 里的调用：

%% ================ Part 2: Gradient Descent ================
alpha = 1.2;
num_iters = 400;

% Init Theta and Run Gradient Descent 
theta = zeros(3, 1);
[theta,J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);

% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');

% Estimate the price of a 1650 sq-ft, 3 br house
% 这里要注意，需要把输入的值进行 normalize，然后才能代入预测方程中
predict_x = [1650,3];
predict_x = (predict_x - mu) ./ sigma;
price = [1, predict_x] * theta;

三、正规方程

　　公式：

　　normalEqn.m 实现：

function [theta] = normalEqn(X, y)
theta = zeros(size(X, 2), 1);
theta = pinv(X' * X) * X' * y
end

　　ex1_multi 里的调用：

%% ================ Part 3: Normal Equations ================

%  predict the price of a 1650 sq-ft, 3 br house.10 data = csvread('ex1data2.txt');   % 重新加载数据
X = data(:, 1:2);
y = data(:, 3);
m = length(y);

% Add intercept term to X
X = [ones(m, 1) X];

% Calculate the parameters from the normal equation
theta = normalEqn(X, y);      % 使用正规方程进行计算25 

28 % ====================== YOUR CODE HERE ======================

price = [1, 1650, 3] * theta; % 预测结果 30 31 % ============================================================

四、测试

 　　运行结果：

Loading data ...
First 10 examples from the dataset:
 x = [2104 3], y = 399900
 x = [1600 3], y = 329900
 x = [2400 3], y = 369000
 x = [1416 2], y = 232000
 x = [3000 4], y = 539900
 x = [1985 4], y = 299900
 x = [1534 3], y = 314900
 x = [1427 3], y = 198999
 x = [1380 3], y = 212000
 x = [1494 3], y = 242500
Program paused. Press enter to continue.
Normalizing Features ...
   1.00000000   0.13000987  -0.22367519
   1.00000000  -0.50418984  -0.22367519
   1.00000000   0.50247636  -0.22367519
   1.00000000  -0.73572306  -1.53776691
   1.00000000   1.25747602   1.09041654
   1.00000000  -0.01973173   1.09041654
   1.00000000  -0.58723980  -0.22367519
   1.00000000  -0.72188140  -0.22367519
   1.00000000  -0.78102304  -0.22367519
   1.00000000  -0.63757311  -0.22367519
   1.00000000  -0.07635670   1.09041654
   1.00000000  -0.00085674  -0.22367519
   1.00000000  -0.13927334  -0.22367519
   1.00000000   3.11729182   2.40450826
   1.00000000  -0.92195631  -0.22367519
   1.00000000   0.37664309   1.09041654
Running gradient descent ...
Theta computed from gradient descent:
 334302.063993
 100087.116006
 3673.548451

 　　（1）当 α = 0.05，预测一个1650 sq-ft, 3 br house 的房屋的售价。梯度下降和正规方程的预测值不同：

68 Predicted price of a 1650 sq-ft, 3 br house (using gradient descent):
69  $289314.620338
81 
82 Predicted price of a 1650 sq-ft, 3 br house (using normal equations):
83  $293081.464335

　　

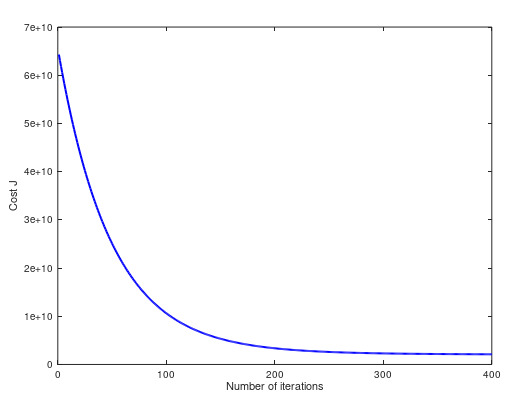
 　（2）当 α = 0.15，cost 曲线如下。两个方法预测值都是   $293081.464335：

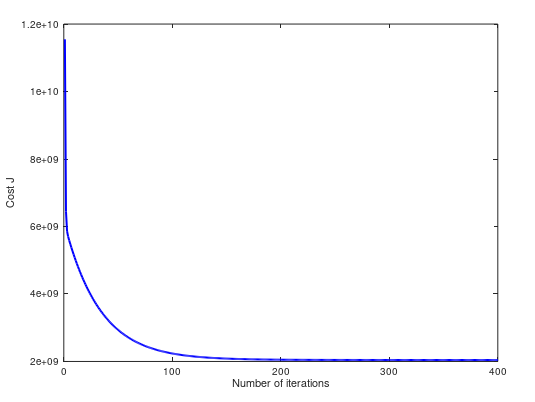
 　（3）当 α = 1，cost 曲线如下。两个方法预测值都是   $293081.464335：

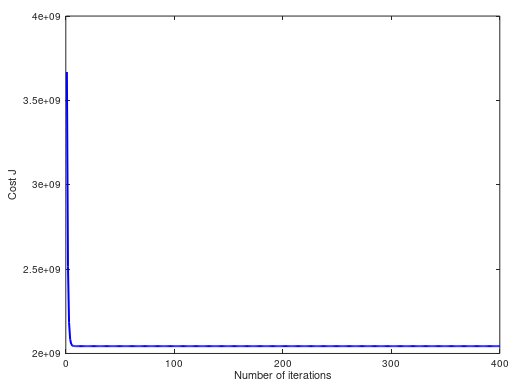
　（4）当 α = 1.2，cost 曲线如下。两个方法预测值都是   $293081.464335：

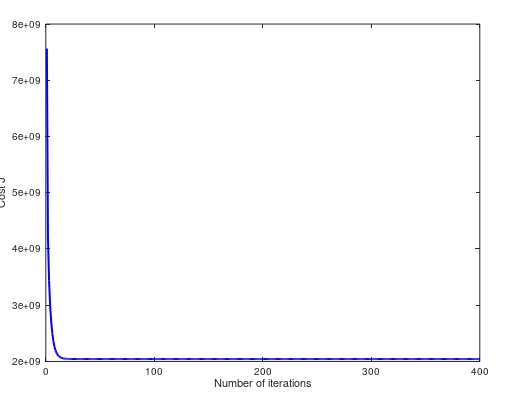
  　（5）当 α = 1.3，cost 曲线如下。两个方法预测值不同 $293157.248289 ，$293081.464335：　

 

　　完整代码：https://github.com/madoubao/coursera_machine_learning/tree/master/homework/machine-learning-ex1/ex1